Файл: 1 Бейсызыты буындарды типтері жне оларды сипаттамалары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 168
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бірінші жолы — тербелмелі жүйеге периодты түрде сырттан әсер етіп, энергияны толықтырып отыру. Механикалық тербелістерде маятникке сырттан периодты күш, ал тербелмелі контурда периодты кернеу әсер етеді. Мұндай тербелістер сыртқы мәжбүр етуші әсердің (күштің немесе кернеудің) жиілігіндей жиілікпен және сондай заңдылықпен жүреді. Бұл — еріксіз тербелістпер. Мысалы, айнымалы электр тогы еріксіз тербеліске жатады, себебі ол тізбекте айнымалы ток генераторынан алынған айнымалы кернеудің әсерінен пайда болады. Біз күнделікті тұрмыста жиілігі 50 Гц айнымалы токты пайдаланып жүрміз. Келесі тарауда айнымалы токты толық қарастырамыз.
Өшпейтін тербелістердің екінші түрі — автпотербелістер. Олар еріксіз тербелістерден сыртқы периодты әсерді қажет етпейтінімен ерекшеленеді.
Автотербелістік немесе өздігінен қозатын процестер табиғатта және техникада кеңінен таралған, және: скрипканың дауысы, есіктің, плотинаның, трамвайдың, тежегіштің бұрылыстағы бекіткіш тетіктерінің сықыры, электроберіліс желісінің "шоқырақтауы", ұшақтағы және аспалы көпірлердегі аэродинамикалық күш әсерінен болатын флаттер құбылысы, автокөлік доңғалақтарындағы "шимми" құбылысы; көптеген машиналардың подшипниктері мен подпятниктеріндегі автотербелістер, металл кесетін станоктардағы, оның ішінде технологиялық машиналардағы және басқа автотербелістер өте тұрақты болады.
Практикада машиналардың жұмысындағы тұрақты процестің бұзылуы кезінде және прокаттық станоктардың, крандардың жүретін доңғалақтарының, т.б. жұмыс органдарының бұзылыстары кезінде көп жағдайда, біліктердің, берілістердің, шпиндельдің және жетектің басқа бөлшектерінің бұзылыстары байқалады. Қарқынды автотербеліс крандардың, арбалардың, қайта тиегіштердің, тиегіш машиналардың механизмдерінде, прокаттық станоктарда, металл кесетін араларда, манипуляторларда, пеш итергіштерінде т.б. қозады. Автотербеліс гармониялық және релаксациялық немесе меншікті тербелістен үлкен, кезеңдермен бөлінген. Көп машинаға авторлардың жасаған эксперименттері, автотербеліс амплитудасының мәні статистикалық жүктемемен салыстырғанда Ма/Мс=0,2÷1,5, ал тербеліс жиілігімен кезеңдері соған сәйкес υ=6-200 1/с, Т=0,03÷1 с шегінде болатынын көрсетті. Механикалық автотербелістің қозу табиғаты өте күрделі. Ең көп қолданылатын теориялардың бірі - сырғанау жылдамдығы функциясындағы (υ)үйкеліс күшінің төмендеуі (μ .үйкеліс коэффициенті) (40 а сурет). Жұмыстағы машинаның автотербелісі кезіндегі кедергі күшінің моменті түрдің кубтық параболасымен аппроксимирленуі мүмкін.
-
Бейсызықты жүйенің өтпелі процесінің графигін фазалық траектория бойынша тұрғызу
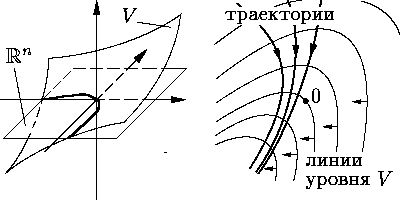
Фазалық жазықтық әдісі реті екіншіден жоғары емес сызықтық емес жүйелерді талдау үшін қолданылады. Координаттары бар жазықтықта және жүйенің қателігі немесе басқа сигнал болған жерде жүйенің траекториясы құрылады. Жүйелердің жазықтығы мен траекториясы фазалық деп аталады. Фазалық траекторияның сипаты бойынша жүйенің сапасы бағаланады.
Фазалық жазықтық әдісі сызықтық емес өздігінен жүретін зеңбіректерді зерттеу үшін қолданылады, олардың сызықтық бөлігі практикалық есептерді шешуге жеткілікті дәлдікпен екінші ретті дифференциалдық теңдеумен сипатталуы мүмкін.
Фазалық жазықтық дегеніміз-оның өзгеру жылдамдығының функциясындағы айнымалы шаманың өзгеруін көрсететін жазықтық:. Фазалық жазықтықта уақыт осі жоқ, бірақ уақыттың әр сәті белгілі бір нүктеге (сурет нүктесі) сәйкес келеді, оның абсциссасы мен ординаты сигналдың мәні мен белгілі бір уақытта оның өзгеру жылдамдығына сәйкес келеді. Уақыт өзгерген кезде кескін нүктесі фазалық траектория деп аталатын белгілі бір траектория бойымен қозғалады.
Амплитудасы мен жиілігі бар Өшпейтін гармоникалық тербелістер болып табылатын сигнал үшін фазалық траекторияның өрнегін анықтаймыз (сурет. 8.6, а):
. (8.1)
Мұндай сигналдың өзгеру жылдамдығы:
. (8.2)(8.1) және (8.2) и
теңдеулерден және негізгі тригонометриялық сәйкестілік негізінде біз аламыз:
. . (8.3)21. Орнықтылық ұғымы. «Аз», «үлкен» және «толық» орнықтылық
Орнықтылық– жүйелердің қозғалысын сипаттайтын параметрлердің
ұзақ уақыт сақталуы. Орнықтылық мәселелері барлық физика, механика, химия, т.б. құбылыстарды зерттегенде туады. Мысалы, механикалық қозғалыстағы орнықтылықты зерттеген Ж.Лагранж (1736 – 1813), П.Лаплас (1749 – 1827), Е.А. Ляпунов (1857 – 1918), С.Пуассон, Н.А. Жуковский (1847 – 1921), Б.Якоби (1801 – 74), т.б. ғалымдар jрнықтылықтың әр түрлі анықтамасын берген. Солардың ішінде орнықтылықтың ең жалпы, қолайлы анықтамасын беріп, математикалық теориясын жасаған Ляпунов болды. Ляпуновтың теориясы бойынша жүйе орнықтылық күйде болу үшін жүйенің аз қозуынан (жүйеге аз энергия берілгенде) оның келесі уақыт ішінде орнықтылық күйден ауытқытуы аз болуы шарт. Осы жағдайда жүйе өзінің орнықтылық күйіне қайта келеді. Консервативті жүйелер орнықтылық күйде болу үшін олардың потенциалдық энергиясы минимум мәнінде болуы керек.
22. Орнықтылық анықтамасы. Ляпунов функциясы
Орнықтылық– жүйелердің қозғалысын сипаттайтын параметрлердің ұзақ уақыт сақталуы. Орнықтылық мәселелері барлық физика, механика, химия, т.б. құбылыстарды зерттегенде туады. Мысалы, механикалық қозғалыстағы орнықтылықты зерттеген Ж.Лагранж (1736 – 1813), П.Лаплас (1749 – 1827), Е.А. Ляпунов (1857 – 1918), С.Пуассон, Н.А. Жуковский (1847 – 1921), Б.Якоби (1801 – 74), т.б. ғалымдар jрнықтылықтың әр түрлі анықтамасын берген. Солардың ішінде орнықтылықтың ең жалпы, қолайлы анықтамасын беріп, математикалық теориясын жасаған Ляпунов болды. Ляпуновтың теориясы бойынша жүйе орнықтылық күйде болу үшін жүйенің аз қозуынан (жүйеге аз энергия берілгенде) оның келесі уақыт ішінде орнықтылық күйден ауытқытуы аз болуы шарт. Осы жағдайда жүйе өзінің орнықтылық күйіне қайта келеді. Консервативті жүйелер орнықтылық күйде болу үшін олардың потенциалдық энергиясы минимум мәнінде болуы керек.
Ляпуновтың функциялары - тұрақтылығын дәлелдеуге арналған скаляр функциялар тепе-теңдік ODE туралы. Деп аталған Орыс математик Александр Михайлович Ляпунов, Ляпуновтың функциялары (Ляпуновтың тұрақтылықтың екінші әдісі деп те аталады) маңызды тұрақтылық теориясы
туралы динамикалық жүйелер және басқару теориясы. Осындай тұжырымдама жалпы мемлекеттік кеңістік теориясында пайда болады Марков тізбектері, әдетте Фостер-Ляпунов деген атпен жұмыс істейді.
ODE-дің белгілі бір сыныптары үшін Ляпунов функциясының болуы тұрақтылықтың қажетті және жеткілікті шарты болып табылады. ODE үшін Ляпунов функцияларын құрудың жалпы әдістемесі болмағанымен, көптеген жағдайларда Ляпунов функцияларын құру белгілі. Мысалы, квадраттық бір күйі бар жүйелер үшін функциялар жеткілікті; нақты шешімі матрицалық сызықтық теңсіздік сызықтық жүйелер үшін Ляпуновтың функцияларын ұсынады; және сақтау заңдары үшін Ляпуновтың функцияларын құру үшін жиі қолдануға болады физикалық жүйелер.
Автономия үшін Ляпунов функциясы динамикалық жүйе
тепе-теңдік нүктесімен у = 0 Бұл скалярлық функция { displaystyle V: mathbb {R} ^ {n} to mathbb {R}} үздіксіз, үздіксіз туындылары бар, қатаң позитивті және ол үшін { displaystyle - nabla {V} cdot g} сонымен қатар қатаң позитивті. Бұл шарт { displaystyle - nabla {V} cdot g} қатаң позитивті болып кейде аталады { displaystyle - nabla {V} cdot g} «жергілікті позитивті анықтама», немесе { displaystyle nabla {V} cdot g} «жергілікті теріс анықталған» болып табылады.23. Орнықтылық жөніндегі Ляпунов теоремасы
Егер жүйенің теңбе-теңдік қалпы x = 0 нүктесінің кейбір U аймағында V (x) Ляпунов функциясы бар болса, онда x = 0 теңбе-теңдік қалып Ляпунов мағынасында орнықты болады.Дəлелдеуі. V (x) функциясы анықталған оң таңбалы болсын. x = 0 нүктесінің Uаймағында шарын қарастырайық. -сол шардың сферасы (шекарасы) болсын,
. -- шектелген тұйық жиын болғандықтан, ал V (x) - үздіксіз функция болғандықтан, əрі V (x) > 0 деп алынғандықтан,
Енді шарын алайық. V (0) = 0 болғандықтан, δ > 0 санын соншалықты кіші етіп алуға болады жəне сол δ үшін
V (x) < K, x.
Енді егер ≤δ деп алсақ, онда ≤ε болатынын көрсетейік (0 ≤ t < ∞) .
U аймағында V ( x) ≤ 0
V(x) болғандықтан, яғни V (x) монотонды өспейтін функция болғандықтан, V ( ) < K жəне кез келген 0 ≤ t < ∞ аралығында x = x(t, ) шешімінің бойында V(x) < K теңсіздігі орындалады. Сондықтан, шарының ішінен басталатын траектория шарынан шығып кете алмайды, өйткені x болғанда V (x) ≥ K , ал траектория бойында V (x) < K . Осыдан ≤ε болатынын көреміз, яғни нөлдік шешіморнықты.
24. Ляпуновтың асимптотикалық орнықтылық жөніндегі теоремасы
асимптотикалық таралу Бұл ықтималдықтың таралуы бұл белгілі бір мағынада бөлудің бірізділігінің «шектеулі» таралуы. Асимптотикалық үлестіру идеясының негізгі қолданыстарының бірі - жуықтамаларды қамтамасыз ету кумулятивті бөлу функциялары статистикалық бағалаушылар.
Тарату тізбегі а-ға сәйкес келеді жүйелі туралы кездейсоқ шамалар Змен үшін мен = 1, 2, ..., I. Қарапайым жағдайда, асимптотикалық үлестіру бар, егер ықтималдық үлестірімі болса Змен ықтималдық үлестіріміне (асимптотикалық үлестірім) сәйкес келеді мен ұлғаяды: қараңыз таралудағы конвергенция. Асимптотикалық таралудың ерекше жағдайы - кездейсоқ шамалардың тізбегі әрқашан нөлге тең немесе Змен = 0 ретінде мен шексіздікке жақындайды. Мұнда асимптотикалық таралу а деградациялық таралу, нөл мәніне сәйкес келеді.
Алайда асимптотикалық үлестіру термині қолданылатын әдеттегі сезім кездейсоқ шамалар пайда болады Змен кездейсоқ емес мәндердің екі тізбегімен өзгертілген. Осылайша, егер үлестірілімде екі реттілік үшін деградацияланбаған үлестіруге жақындайды {амен} және {бмен} содан кейін Змен бұл асимптотикалық үлестірім ретінде осы үлестіруге ие дейді. Егер асимптотикалық үлестірімнің таралу функциясы болса F содан кейін үлкен үшін n, келесі шамалар орындалады. Егер асимптотикалық үлестіру болса, кездейсоқ шамалар тізбегінің кез-келген нәтижесі сандардың конвергентті тізбегі екендігі міндетті емес. Бұл жинақталатын ықтималдықтардың үлестірілуінің кезектілігі.
25. Орнықсыздық жөніндегі Ляпунов теоремасы
Ляпуновтың V жүйесінің (4) функциясы (5) қанағаттандырсын және нөлдік тепе-теңдік позициясының кез-келген маңында ол теріс болатын нүктелер бар. Содан кейін бұл жүйенің нөлдік шешімі тұрақсыз. Бұл теореманың геометриялық мәні суретте көрсетілген.
