Файл: 1 Бейсызыты буындарды типтері жне оларды сипаттамалары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 172
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
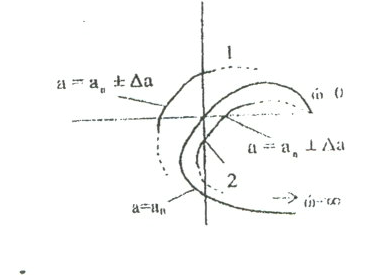
6.2-сурет. Михайлов қисығы
Периодты шешімнің тұрақтылығын зерттеу үшін амплитудаға аздаған үстеме (приращение) береміз.
1) Егер Δа>0 болса, Михайлов қисығы 1 күйде болады, ал Δа<0 -2 күйде, онда жүйедегі өтпелі процесс былай болады: ап -нен үлкен амплитудамен тербеліс өшеді, ал ап -нен кіші амплитудалы тербеліс ажырайды. Сонымен, екі жақтағы өтпелі процесс зерттелетін периодты режимге келеді, яғни жүйеде амплитудасы бар автотербеліс орын алады.
2) Егер Δа>0 кезінде 2 қисық, ал Δа<0 кезінде 1-ші қисық алынса, онда зерттелетін периодты шешім тұрақсыз. Жүйе аз уақытта тұрақты, үлкен уақытта тұрақсыз.
0>0>
Найквист критерийі негізінде автотербелісті есептеу
Бұл әдісті совет ғалымы Л.С.ГНӘьдфарб ойлап тапқан.
Бейсызықты ашық АБЖ келесі түрде болсын:
6.3-сурет. Бейсызықты ашық АБЖ
мұнда
(6.9)
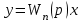(6.10)Гармоникалық сызықтау формуласына сәйкес
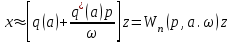(6.,11) Бейсызықты буынның комплексті берілу коэффициенті деген ұғым енгіземіз. НӘ
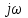кезінде беріліс функциясынан алынады және кірісінде тербеліс амплитудасына ғана тәуелді болады.
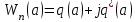(6.12)Берілудің комплексті коэффициенті немесе жүйенің сызықты бөлігінің жиілікті берілу функциясы:
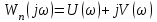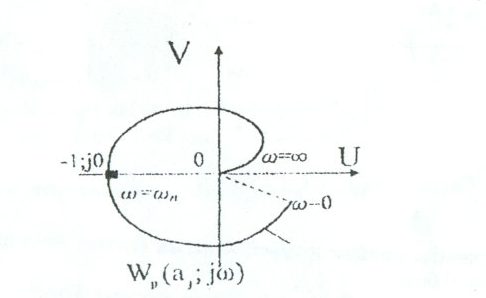
(6.13)Жалпы эквивалентті жиілікті беріліс функциясы немесе АФЧХ ашық жүйесі мынандай болады:
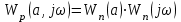(6.14)Тұйықталған жүйедегі өшпейтін тербеліс Найквист критерийіне сәйкес АФЧХ ашық жүйесінде
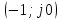нүктесі арқылы өтумен анықталады, яғни келесі теңдікпен: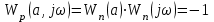
(6.15) 
6.4-сурет. АФЖС
Бұл тұйықталған бейсызықты жүйе үшін периодты шешімнің бар болу шарты болады.
(6.15) теңдеуін мына түрге келтіруге болады:
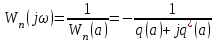(6.16)Соңғы теңдеу графикалық жолмен шешіледі. Бұл үшін жеке СБ АФЖС жүйесін және (-)белгісі есебінен кері АФЖС бейсызық буынын тұрғызу керек (6.5-сурет).
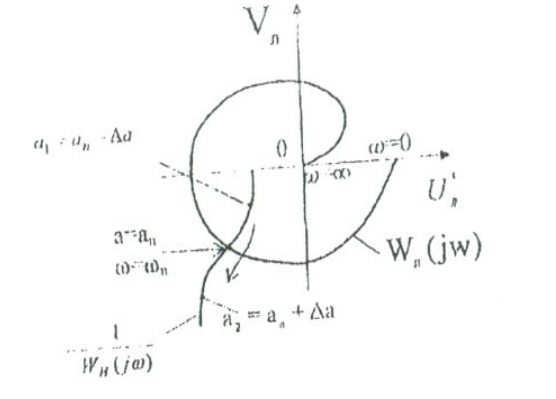
6.5-сурет. Сызықты бөліктің АФЖС
Бұл екі сипаттамалардың қиылысу нүктесі (6.5-сурет) теңдеуі шешімен анықталады.
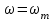жиілік периодты шешімі сызықты бөлімнің
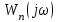годографындағы жиілік белгілеуі бойынша, ал а=аn амплитуда бейсызықты буынның
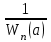годографындағы амплитуда белгіленуі бойынша анықталады.Жүйенің сызықты бөлімі ашық жүйеде тұрақты немесе бейтарап. Онда периодты шешім кейбір
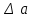тиімді үстеме (приращение) береміз. Бұл үшін годограф бойынша БЗ қиылысу нүктесі амплитудасының (
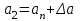нүктесі) өсуі жағына қарай қозғаламыз. Бұл 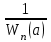модулі өсуімен сәйкес немесе 
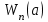модулінің төмендеуімен.Нәтижесінде
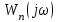
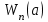туындысы модуль бойынша төмендейді және АФЖС ашық жүйесі 
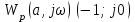нүктесі арқылы өтпейтін болады. Бұл жағдай тұрақтылығы өшетін процесінде, яғни тербеліс амплитудасы төмендейтін кезіне сәйкес келеді.Амплитуданың төмендейтін жағдайында
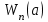модулінің ұлғаюы жүреді және нәтижесінде–АФЖС қамту нүктесі
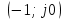тұрақсыздықтың пайда болуы және тербеліс тербеліс амплитудасының ұлғаюы басталады.Сонымен, тербеліс амплитудасының a=an+∆ ауытқуының барлық жағдайлары кезінде, ол өзінің аn мәнін қалыптастырады. Яғни, периодты шешім тұрақты болады және автотербеліспен сәйкестенеді.
Қалыптасқан критерийді жеңілдетуге болады:
Периодты шешім тұрақтылығы үшін 6.5-суретте көрсетілгендей
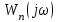ішкі годограф облысының сыртқы 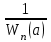годографына өтуі кезінде амплитуданың өсуінің жүруі талап етіледі. Егер мұндай өту кезінде амплитуда мәнінің өшуі болса, онда периодты шешім тұрақсыз.СБ мен БЗ годографтары бірнеше нүктелерде қиылысатын күрделі жағдайларыда кездеседі (6.6-сурет).
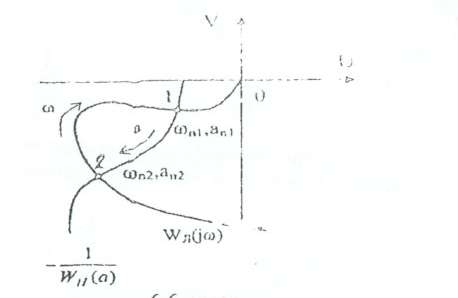
6.6-сурет. Сызықты бөлік пен бейсызықты бөліктің годографтарының қиылысуы
Бұл жағдайда
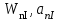және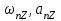
параметрлерінен екі периодты шешімі болуы мүмкін.-
Берілген параметрлері бойынша импульстік сүзгінің беріліс функциясын анықтау
Сүзгі синтезі деп біз жоғарыда айтылған сигнал мен шу қатынасының максималдылығын қамтамасыз ететін физикалық мүмкін болатын сүзгінің тасымалдау функциясын табуды айтамыз. Тасымалдау функциясы пішінде көрсетіледі.
Осылайша, мәселе оңтайлы сүзгінің жиілік реакциясы мен фазалық реакциясын табуға дейін төмендейді. Бұл мәселе біркелкі спектрі бар ақ шу фонында жұмыс істейтін сигнал үшін оңай шешіледі.
Оңтайлы (көрсетілген мағынада) беру функциясын табу үшін сүзгі шығысындағы сигнал мен шу үшін алдымен бөлек, содан кейін олардың қатынасы ретінде өрнектерді құрастырамыз.
Белгіленген уақыт нүктесіндегі сигнал жалпы өрнекпен анықталады.
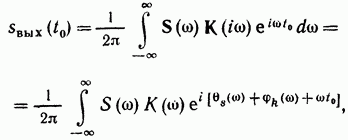
және интерференцияның орташа квадраттық мәні – өрнек бойынша
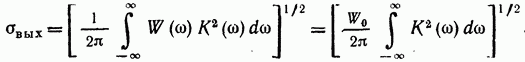
Өрнекте – берілген кіріс сигналының спектрлік тығыздығы, ал асты – фильтр шығысындағы сигналдың максимумына (шыңына) сәйкес келетін уақыт нүктесі (әлі анықталмаған) дегенді білдіреді. Мағынасы мен мүмкін болатын ең төменгі мән келесі абзацта толығырақ қарастырылады, алайда қарапайым идеялардан шыңы сигналдың барлық энергиясын пайдалануды талап ететіні анық және бұл кірістің соңына дейін мүмкін емес. сигнал. Басқаша айтқанда, ол сигналдың аяқталуынан ерте болуы мүмкін емес. Енді қарым-қатынас жасайық
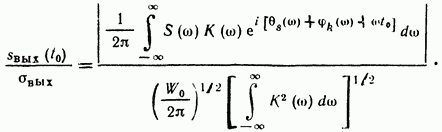
Біз белгілі Шварц теңсіздігін қолданамыз
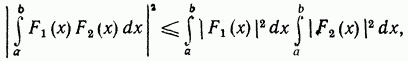
мұнда, жалпы жағдайда, күрделі функциялар.
Бұл теңсіздік шарт болған кезде ғана теңдікке айналады
яғни, функция күрделі конъюгаттық функцияға пропорционал болғанда (A - ерікті тұрақты коэффициент).
(13.4) және -де теңестіріп, (13.4) теңсіздікті түрінде жазамыз
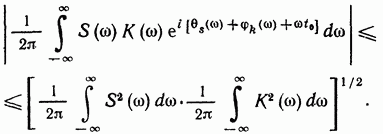
Сонда (13.3) өрнек келесі теңсіздікті құруға мүмкіндік береді:
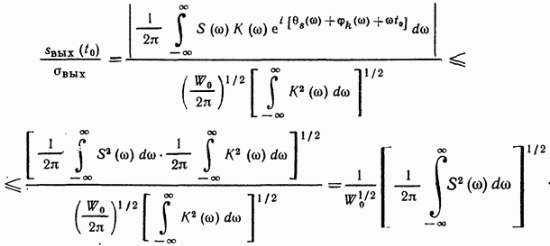
Осы теңсіздіктің оң жағындағы төртбұрышты жақшадағы өрнек кіріс сигналының Е толық энергиясынан басқа ештеңе емес [қараңыз. (2.66)], біз келесі нәтижеге келеміз:
Соңында (13.5) өрнектен шарт орындалғанда бұл теңсіздік теңдікке айналатыны шығады
немесе не бірдей
Алынған қатынас сүзгінің тасымалдау функциясын толығымен анықтайды, ол шығыстағы сигнал-шуыл қатынасын барынша арттырады (ақ шу сияқты кіріс шуымен).
(13.8) шартқа сәйкес функция сигналдың спектрлік сипаттамаларына — амплитудасы мен фазасына сәйкес келеді. Осыған байланысты қарастырылатын оңтайлы сүзгіні жиі сәйкес келетін сүзгі деп атайды.
Сонымен, сәйкес сүзгі шығысындағы шудың RMS мәніне сигнал шыңының қатынасы теңдікпен анықталады.
Қатынастар (13.8) сәйкес сүзгіге келесі екі талапты білдіреді:
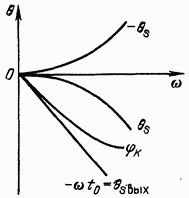
Күріш. 13.2. Сәйкес фильтрдің кірісі мен шығысындағы сигнал спектрінің фазалық сипаттамалары арасындағы байланыс
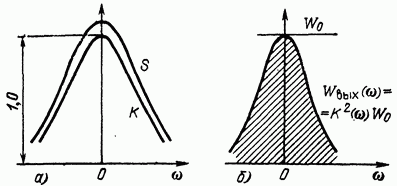
Рис. 13.3. Сигналдың спектрлік тығыздығы және сәйкес сүзгінің жиілік реакциясы (a) және сүзгінің кіріс және шығысындағы энергия спектрлері (b)
Сүзгінің АЧХ шартқа сай болуы керек
АЧХ шартқа сай болуы керек
Күрделі беріліс функциясы өлшемсіз шаманы білдіретін жағдайларда (мысалы, шығыс және кіріс кернеулерінің күрделі амплитудаларының қатынасы) тұрақты А коэффициенті сигнал спектрлік тығыздығының өлшеміне кері болатын өлшемге ие болуы керек.