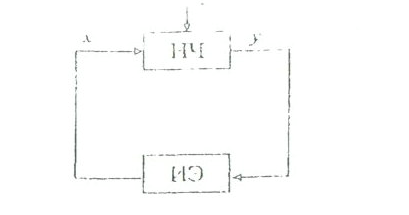
7.1-сурет. Тұйықталған импульстік АБЖ

Мұнда ҮБ-жүйенің үздіксіз бөлімі, ал ИЭ импульсті элемент.

ИЭ уақыт бойынша Х үздіксіз сигналды У дискретті сигналға кванттауды іске асырады.

Үздіксіз сигналдың импульстер тізбектілігіне түрлендіру түріндегі ИЭ-мен іске асырылатын кванттау импульстік модуляция деп талады.

ИЭ-нің шығыс сигнал үшбұрышты түрде болады және келесі параметрлермен сипатталады (7.2-сурет).



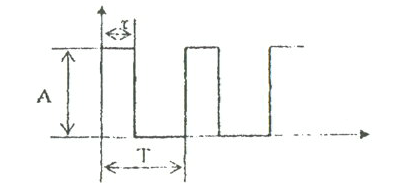
7.2-сурет. Шығыс сигналының сипаттамасы

-А импульсінің биіктігімен немесе амплитудасымен;

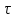- импульсінің ұзақтығымен немесе кең жолағымен;

-Т импульсінің қайталану периодымен;

-Т- көрші импульсінің арасындағы үзілісімен;

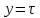/Т тік өзектілігімен(скважностью).

Импульсті модуляция кезіндегі үзілісссіз сигналдың импульстер тізбегіне түрлендіру процесінде көрсетілген импульстік параметрлері шығыстық әсерлесу функциясында өзгеріп тұруы мүмкін.

Импульсті шығыс параметрлерінің қайсысы өзгеріске ұшырағанына байланысты импульстік модуляцияның үш түрін бөлуге болады АИМ,ШИМ,ЧИМ.

импульстік модуляцияның басқа да түрлері бар, алайда Олар байланыс жүйелерінде ғана қолданылады, сондықтан бұнда қарастырымайды.

---

39. Дискретті жүйені импульсті түзету

Дискретті жүйеде үздіксіз сигналдарды үзетін элемент және Оларды дискреттіге түрлендіреді.

Үздіксіз сигналдардың дискретті сигналдарға түрлену процесі кванттау деп аталады.

Сигналдардың кванттауының үш әдісі бар:

а) деңгейі бойынша;

б) уақыт бойынша;

в) аралас деңгейі және уақыт бойынша.

Кванттау типіне байланысты дискретті жүйелер релелік (деңгейі бойынша кванттау), импульстік(уақыт бойынша) және цифрлік (аралас) болып бөлінеді.

Дискретті АБЖ кең қолданыс тапты, Олар жоғары дәлдікпен және аналогты берілгендердің сандық көрсетілуі есебінен бөгеуілден қорғаушылықпен сипаттаталады

Дискретті жүйенің смпаттама аппараты негізіндегі торлы функция түсінігі дифференциалды теңдеудің дискретті аналогқа-айырымды теңдеуге көшуді іске асыруға мүмкіндік береді.

Үздіксіз функцияның аналогты туындысы торлы функция үшін айырымды болып келеді. Бірінші айырым (1-ретті айырым) торлы функцияның өзгеру жылдамдығынт сипаттайды және үздіксіз функцияның бірінші туындысының аналогы болып келеді.

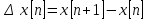(7.1)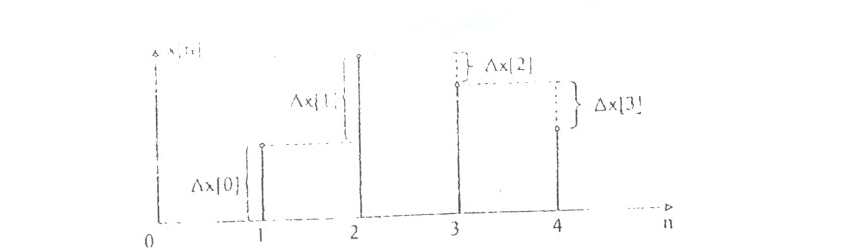



7.6-сурет. Торлы функцияның бірінші дәрежелі айырмасы

7.6-сурет торлы 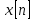функцияның бірінші айырымы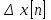

40. Автоматты басқару жүйесіндегі сандық жүйелердің ерекшелігі

АБТ-да оқылатын сызықты жүйелер белгілі бір формадағы анықталған бейсызықты тәуелділіктері бар болатын нақты жүйелерді сызықтау нәтижесінде алынады. Дегенмен, бір немесе бірнеше буындарда Олардың құрамында қомақты бейсызықтылардың болуынан немес қомақты бейсызықтылар жүйеге арнайы күтілетін қасиеттерді алу үшін енгізілетіндіктен, сызықтауды жүргізу мүкіндігі болмайтын жағдайлар кездеседі.

Бейсызықты жүйе деп бейсызықты дифференциалдық немесе алгебралық теңдеулермен сипатталатын жүйе аталады. Әдетте, бейсызықты жүйе кем дегенде бір бейсызықты буынның, яғни бейсызықты дифференциалдық теңдеулермен сипаттаталатын буындардың бар болуы нәтижесінде алынады.

Бейсызықты жүйелерге келесілері жатады:

---

1. 
   релелі сипаттамасы бар буын
   
2. 
   бөлшекті-сызықты типті сипаттамасы бар буын
   
3. 
   Қисық сызықты сипаттамасы бар буын
   
4. 
   теңдеу құрамына кіретін айнымалылар мен туындыларының көбейтіндісінен тұратын бейсызықты теңдеулерлермен сипатталатын буын.
   
5. 
   жұмысы логикалық операцияларды орындаумен байланысты буын.
   

Сызықты емес АБЖ-сі процестері сызықты жүйелерде кездеспейтін бірқатар ерекшеліктері бар. Олардың қатарына келесілері жатады:

1. 
   Бұл жерде тұрақтылық түсінігі өте күрделі. Жүйенің бастапқы шарттары жүйе тұрақтылығына әсер ету жағдайында да болуы мүмкін. Мысалы, тепе-теңдік жағдайынан сәл ауытқу кезінде жүйе тұрақты болуы мүмкін, яғни процесстер сәйкестенуші болады, ал үлкен ауытқуда жүйе тұрақсыз уақыт бойынша таратылған (шашыратылған). Кері жағдайлар да болуы мүмкін. Осыдан жүйенің тепе-теңдік жағдайынан «аз» және «көп» ауытқуларына байланысты сызықты емес жүйелерде «аз» мәнді тұрақтылық және «үлкен» мәнді тұрақтылық түсінігі енгізіледі.
   
2. 
   Сызықты емес жүйеледе автотербеліс деп аталатын орнықталған режимнің жаңа түрі болуы мүмкін. Автотербелісті сыртқы тербеліс әсерлері болмаған жағдайда тұрақты жиілігі мен тұрақты амплитудасы бар қалыпты өзіндік тербеліс ретінде түсінуге болады.
   
3. 
   Сызықты емес жүйелерде суперпозиция принципі қолданылмайтындықтан, НӘ басқа факторлар әсерінен туындайтын құраушылар қосындысы сияқты шығыс шамасын анықтаудың мүмкін болмауы.
   

1. 
   Сандық автоматты басқару жүйесінің динамикасын зерттеу
   

Сандық автоматты басқару жүйесіндегі (DPC) сандық есептеуіш құрылғылардың әртүрлі түрлері соңғы уақытта әртүрлі автоматты басқару жүйелерінде кеңінен қолданыла бастады. Цифрлық ЭЕМ-нің кең мүмкіндіктері оларды басқару процесінің жоғары сапалы көрсеткіштеріне қол жеткізу үшін автоматты жүйелерде пайдалануға мүмкіндік береді. Цифрлық компьютерді басқару цикліне қосу үздіксіз процестерді дискретті және кері түрлендірулерге түрлендіруге мүмкіндік беретін қосымша көмекші құрылғыларды қажет етсе де, бүкіл жүйені тұтастай ететін кез келген дерлік басқару заңын жүзеге асыру мүмкіндігімен өтеледі және өте тиімді.



Динамикалық тұрғыдан алғанда цифрлық жүйелер уақыт бойынша да, деңгейде де сигналдың квантталуының болуымен сипатталады. Мұндай жүйелер сигналдың импульстік-кодтық модуляциясымен сипатталады. Деңгейдің кванттауының болуы цифрлық жүйеге мәні бойынша сызықтық емес сипат береді, бірақ көп жағдайда, мысалы, жүйеде көпразрядты цифрлық датчиктер пайдаланылғанда, деңгейдің кванттау әсерін елемеу және цифрлық жүйені сигнал уақыт бойынша ғана квантталатын импульстік жүйе ретінде қарастырылады.

---

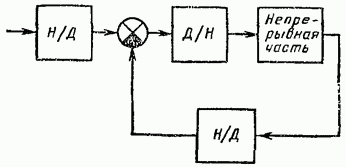
Цифрлық жүйенің (ЦС) жалпыланған блок-схемасы күріште көрсетілген формада берілген. 8.26. Мұндағы белгі үздіксіз сигналды дискреттіге түрлендіруге арналған құрылғыны білдіреді. Түрлендіргішті көп сатылы деңгейлі кванттау элементінің (8.27-сурет) және амплитудалық-импульстік модуляцияны орындайтын импульстік элементтің тізбекті қосылымы ретінде көрсетуге болады [6] (8.28-сурет).

Таңба дискретті сигналдарды үздіксіз сигналдарға түрлендіруге арналған құрылғыны көрсетеді (8.26-сурет). Оны (8.4) өрнекпен анықталған тасымалдау функциясы бар нөлдік ретті фиксатор болып табылатын қалыптаушы құрылғы ретінде көрсетуге болады. PS циклі сонымен қатар тасымалдау функциясы бар басқару объектісін (үздіксіз бөлігі) қамтиды (8.28-сурет).

Суретте көрсетілген схеманы жеңілдетіңіз. 8.28, әрекет пен кері байланыс тізбегінен импульстік элементті қателік тізбегіне ауыстыру (8.29-сурет). Суреттегі диаграммадан. 8.29, егер деңгейді кванттау назардан тыс қалса, онда DS блок-схемасы (8.29-сурет) AIM бар жүйенің құрылымдық схемасымен толығымен сәйкес келетіні анық.



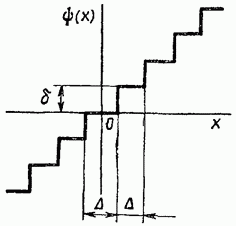
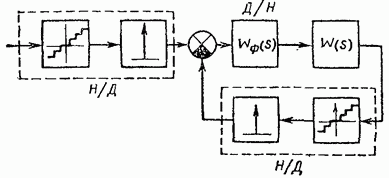
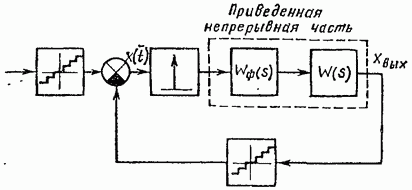
рис. 8.12). Демек, деңгейлік кванттауды есепке алмай CS зерттеу үшін AIM бар жүйені зерттеу үшін алынған алдыңғы бөлімнің барлық нәтижелері жарамды.

Бұл бөлімде тарауда сызықты үздіксіз жүйелерді зерттеу үшін сәтті пайдаланылған логарифмдік жиілік сипаттамалары аппаратын қарастырған жөн. Осы оқулықтың 3-5. Бұл мәселе CS және AIM жүйелерінің тұрақтылығын зерттеуде өте өзекті, өйткені кең таралған Nyquist критерийін қолдану ашық жүйенің жиілік реакциясын құруды талап етеді, бұл инженерлік есептеулер тәжірибесінде айтарлықтай қиын болуы мүмкін.

2. 
   Ерекше нүктелер мен ерекше қисықтарды қамтитын фазалық кескіндер
   

Абсцисса осінің қандай да бір нүктесіндегі интегралдық қисыққа жанама арқылы түзілген еңістің тангенсі осы нүктенің мәнін анықтайды. FP нүктелерінің жиыны , изоклиналы деп аталады. ФП-ға көптеген изоклинальдарды салуға болады, олардың әрқайсысының өзіндік мәні бар.

Екінші ретті тізбектегі процестерді көрсететін ФП барлық нүктелері үшін (сингулярлық нүктелерден басқа) нақты анықталған мәнге ие. Ерекше нүктелерде (ОТ), яғни анықталмаған. Осы нүктелер арқылы әртүрлі мәндері бар көптеген изоклиндерді салуға болады.

---

ОТ осы нүктелерді қоршап тұрған интегралдық қисықтардың түріне қарай жіктеледі.

Егер ОТ эллипстермен қоршалған болса (16.11, е-сурет), онда ол орталық типті ОТ деп аталады; ол сипаттамалық теңдеудің екі ойша түбірімен сәйкес келеді.

Егер ОТ ширатылған спиральмен қоршалған болса, онда ол тұрақты фокус деп аталады (16.11, е-сурет) теріс нақты бөлігі бар күрделі конъюгаттық түбірлерге сәйкес келеді.

Егер ОТ орама спиральмен қоршалған болса, онда оны тұрақсыз фокус деп атайды (16.11, ж-сурет) оң нақты бөлігі бар күрделі конъюгаттық түбірлерге сәйкес келеді.

Егер түбірлер теріс және нақты болса, онда ОТ тұрақты түйін деп аталады (16.11, ч-сурет). Оң нақты түбірлермен тұрақсыз түйін түріндегі ОТ алынады (16, і-сурет). Бір түбір оң, екіншісі теріс болса, бізде седла типті ОТ болады (16.11, j-сурет).

Суреттегі тізбектегі өтпелі процесті қарастырайық. 16.12, а, нөлдік бастапқы жағдайларда кілттің жабылуынан туындаған:



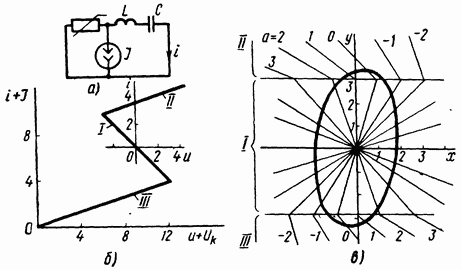
Конденсатордағы кернеу үшін изоклиндер тобын құрайық ОТ орнын және түрін анықтайық. Өтпелі процестің фазалық траекториясын тұрғызайық.

Схема теңдеуінде біз онымен ауыстырамыз және у мен үшін теңдеуді шешетінімізді ескереміз:



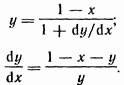
(b) теңдеуінен сингулярлық нүктенің координаталары Мәндерді ретімен бере отырып, изоклиндер тобын құрамыз (16.12, б-сурет). Барлық изоклиндер ОТ арқылы өтеді және түзу сызықтар (тізбек сызықты). Осьтер мен у бойындағы масштабтар бірдей деп есептеледі. Әрбір изоклинальды сызықшалар оның мәнін сипаттайды.

Содан бері процестің басында бейнелеуші ​​нүкте координаталар басында орналасады. тұрақты күйде және

Бастапқы нүктеден интегралдық қисық салу үшін екі сәулені изоклинальмен типті нүктелермен қиылыстырғанша саламыз: Бірінші сәуле қозғалыс басталатын изоклиннің мәніне, екіншісі келесі сәуленің мәніне сәйкес келеді. нүкте қозғалатын изоклин. Біз қашықтықты екіге бөлеміз және бастапқы және қабылданған нүктелер арқылы тегіс қисық сызамыз - фазалық траекторияның бір бөлігі. Біз аналитикалық процесті әрі қарай жалғастырамыз және бүкіл фазалық траекторияны ширатылған спираль түрінде саламыз.

Мысалдағы FROM тұрақты фокус болып табылады. Уақыт фазалық жазықтықта анық көрсетілмейді.

Фазалық траектория бойынша уақытқа тәуелділік формула бойынша алынады

---

Смотрите также файлы

• Контрольнооценочные средства.pdf

• Азиатское происхождение скифов по Геродоту.pptx

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx

• Урок 18 Раздел Мультимедиа (сквозная тема В здоровом теле здоровый дух!) Ф. И. О. учителя Дата.doc

• Контрольная работа на промежуточной итоговой аттестации (12 класс). Фамилия, имя дата.docx