Файл: 1 Бейсызыты буындарды типтері жне оларды сипаттамалары.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 175
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, мұндағы бастапқы мән, ағымдағы мән.
Қисықтың абсцисса осімен қиылысу нүктесінің маңайында интеграл шексіздікке ұмтылады. Шексіздікке баратын қисық астындағы ауданды жоспарлауды болдырмау үшін осы бөлімде уақытты есептеу кезінде орташа жылдамдық есептеледі.
Фазалық кеңістік түсінігі, фазалық траекториялар және олардың түрлері жоғарыда келтірілген. Бұл бөлімде сызықты емес автоматты басқару жүйелеріндегі процестердің кейбір маңызды ерекшеліктері қарапайым екінші ретті жүйелер үшін фазалық траекторияларды құру мысалдарымен суреттелетін болады.
Мысал 1. Өздігінен нивелирленбейтін объектісі бар және тұрақты жылдамдығы бар реттегіш жетекі бар автоматты басқару жүйесін алайық. Өздігінен нивелирленбеген реттелетін объектінің теңдеуі болады Массасы жоқ контроллер және қатты кері байланысы бар амортизатор үшін, яғни үшін біз аламыз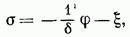
мұндағы - реттелетін шаманың салыстырмалы өзгерістері, сезімтал элементтің, реттеуші органның, кері байланыс элементінің және басқару золотникінің орын ауыстырулары (10.11, а-сурет), - коэффициент. Реттегіш жетегі екі нұсқада тұрақты жылдамдыққа ие болсын; 1) лезде ауысумен (16.22-сурет, ж) басқару элементі (золотник, ағынды түтік) өлі аймақпен бейтарап күйден өткенде (16.22-сурет, h) золотниктің «қабаттасуының» болуына байланысты немесе реактивті түтік. Бірінші жағдайда реттегіш жетектің теңдеуі болады.
Фазалық траекторияларын салу
х-y фазалық жазықтықта фазалық траектория сызғанда оны салудың келесі жалпы ережелерін назарға алған дұрыс.
Фазалық траекториялар y=f(x) фазалық теңдеуі бойынша салынады, оны табудың алдында ең алдымен жүйенің бастапқы дифференциалды теңдеулерінен фазалық траекториясының дифференциалды теңдеуін аламыз.
(2.2)
Бірінші теңдеуді екінші теңдеуге бөле отырып уақыттан арыламыз
(2.3)
Кейбір жағдайларда бұл теңдеу интегралданып, фазалық траекторияның теңдеуі
болып табылады, алынған теңдеу бойынша жүйенің фазалық портреті тұрғызылады.
Қисық-сызықты сипаттамалары бар буындардан тұратын жүйелер үшін, фазалық жазықтықта (2.3) теңдеуінің сондай немесе басқа түрі кездесетін аймақтар белгіленуі мүмкін. Бұл аймақтар ауысып қосу сызықтары деген сызықтармен шектеледі (2.15-сурет).
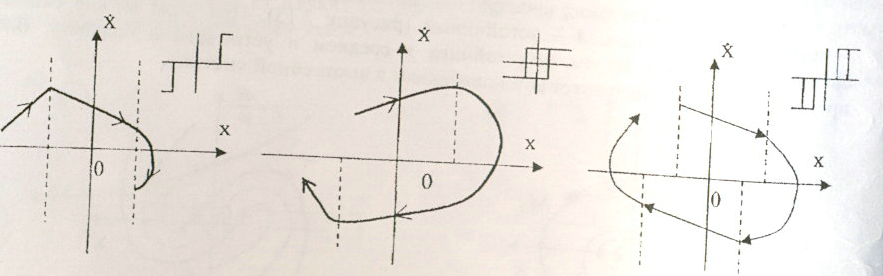
2.15-сурет. Ауысып қосу сызықтарының қарапайым орналасу жағдайлары
(2.3) теңдеуі интегралданбаған жағдайда фазалық траектория салудың жуықталған әдісі бойынша тұрғызылады. Оны изокин әдісі деп атайды.
Ляпунов функцисының оң анықталған түрін аламыз:
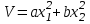(3.9)
мұндағы a,b – кез-келген берілген оң сандар.
V шамасына өспелі тұрақты мәндер береміз: V= 0,C1,C2 … Олар төменгі теңдеулерге сәйкес келеді.
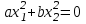
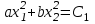
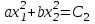(3.10)
…………….
Бұл теңдеулердің біріншісі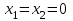
нүктесіне сәйкес келеді, яғни координат басына, ал қалғандары фазалық кеңістіктегі белгілі бір қисыққа сәйкес келеді (3.2-сурет).
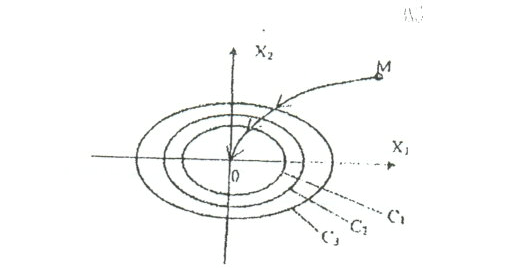
3.2-сурет. Фазалық кеңістік
Егер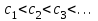
болса, онда әрбір тұйық қисық ішінде координат бас нүктесін және кіші 
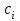-ге сәйкес келетін қисықтар болады. 
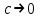болғанда қисықтар координат басына тартылады, яғни 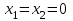нүктесінде ұмтылады. М бейнелеуші нүктенің барлық мүмкін болатын траекториясындағы қозғалысы V функциясының
үлкен мәніне сәйкес қисығынан V функциясының кіші мәніне сейкес қисығына өтетіні бізге белгілі болсын делік.
мысалда Ляпунов теоремаларының дұрыстығын тексерелік.
Екінші ретті жүйені алайық (n=2)
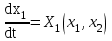(3.8)
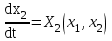
Ляпунов функцисының оң анықталған түрін аламыз:
(3.9)
мұндағы a,b – кез-келген берілген оң сандар.
V шамасына өспелі тұрақты мәндер береміз: V= 0,C1,C2 … Олар төменгі теңдеулерге сәйкес келеді.
(3.10)
…………….
Бұл теңдеулердің біріншісі
нүктесіне сәйкес келеді, яғни координат басына, ал қалғандары фазалық кеңістіктегі белгілі бір қисыққа сәйкес келеді (3.2-сурет).
3.2-сурет. Фазалық кеңістік
Егер
болса, онда әрбір тұйық қисық ішінде координат бас нүктесін және кіші -ге сәйкес келетін қисықтар болады. 
болғанда қисықтар координат басына тартылады, яғни нүктесінде ұмтылады. М бейнелеуші нүктенің барлық мүмкін болатын траекториясындағы қозғалысы V функциясының үлкен мәніне сәйкес қисығынан V функциясының кіші мәніне сейкес қисығына өтетіні бізге белгілі болсын делік.
АБЖ-да сызықты емес тәуелділіктердің бар болуы жүйенің жағдайы сызықты емес дифференциалды теңдеулермен сипатталуына әкеліп соғады. Сызықты емес теңдеулердің көптеген топтары жалпы жағдайда шешілмейтіні белгілі, шешімдердің тек жеке жағдайлары жайында айтуға болады. Сондықтан сызықты емес жүйелерді зерттеуде әр түрлі жуықталған әдістер үлкен рНӘь атқарады.
Сызықты емес жүйелердің зерттеуді жуықталған әдістер арқылы жүйенің барлық динамикалық қасиеттері жайында қажетті толық мәліметтер ала алмаймыз, бірақ Олардың көмегімен арнайы қажетті сұрақтарға жауап берілуі мүмкін, мысалы, орнықтылығы, автотербелістің бар болуы, кез келген жеке режимдер сипаттамалары және тағы басқа.
Бірақ релелі типті жүйелерді (сипаттамалары тек горизонтальді немесе тек вертикальді түзулерден тұратын) сызықты дифференциалды теңдеулер аппараттық қолдану арқылы толық зерттеуге мүмкіндік береді.
Қазіргі кезде сызықты емес жүйелерді зерттеудің түрлі аналитикалық немесе графо-аналитикалық әдістері бар. Олардың ішінде орнықтылықты зерттеудің әдістері көзделген. Оларды екі үлкен топқа бөлген ыңғайлы: нақты және жуықталған.
Релелі элементтердің гармоникалық сызықтау коэффициенттері
(5.10) теңдеуінен q(a) және q/ (a) коэффициенттерін табамыз, кейбір типтік элементтер үшін (5.11) формула бойынша анықтаймыз:
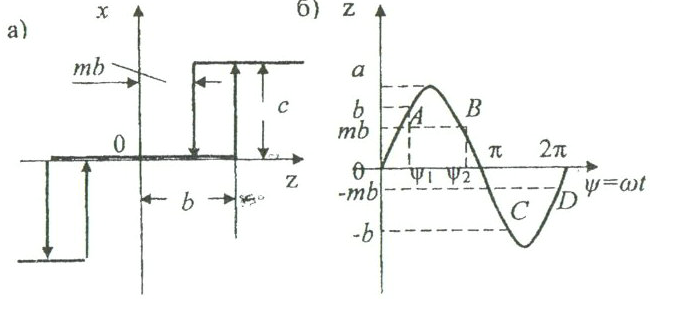
5.3-сурет. Релелі элементтерінің сипаттамасы
БЭ жалпы сипаттама түрін (5.3,а-сурет) аламыз, мұнда m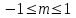
интегралдағы бөлшек сан.
Егер
кіріс шамасының тербелісінің a
.
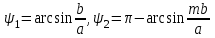(5.13)
Бірнеше көмекші теңдеулер аламыз:
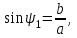
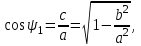
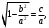
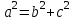
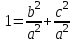
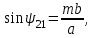
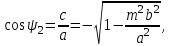
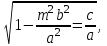
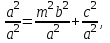
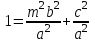
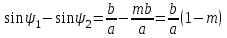
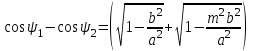
(5.11) интегралында симметриялық сипаттама үшін келесі түрдегі вектормен алуға болады:
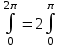
Олардың әрқайсысы үш қосындыға бөлінеді:
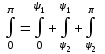
Бірінші және үшінші қосылғыш (5.3а және б-сурет) 0-ге тең болады. Онда (5.10) теңдеуі келесі түрде болады:
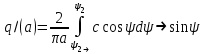
Немесе интегралдап, мынаны аламыз:
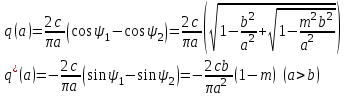(5.14)
Гистеризисті емес түйін сипаттамасымен релелі буын үшін, мұнда (5.14) формуладан т=1болады деп есептеп алатынымыз(5.4-сурет).
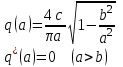
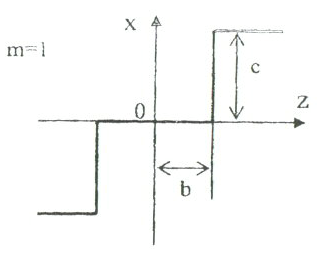
5.4-сурет. Үш позициялы реле
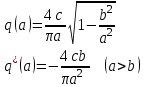(5.15)
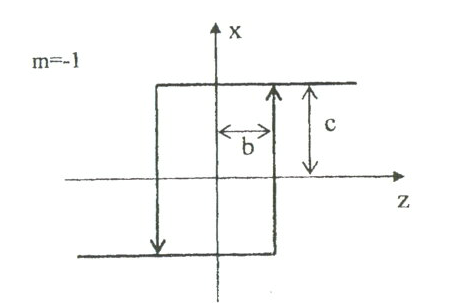
5.5-сурет. Гистеризисі бар реле
Релелі буын үшін b=0 деп есептеп:
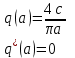(5.16)
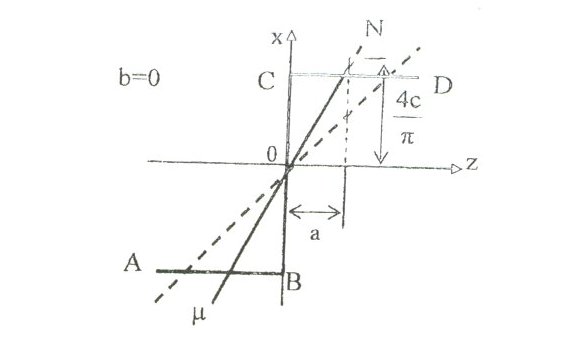
5.6-сурет. Релелі буын
Соңғы мысалдан релелі сипаттаманың гармоникалық сызықтауының мағынасын көруге болдаы. Бұдан a берілген амплитуда мен қиылысатын MN тік сызықты ABCD сынық бөлігін шамамен алмастырып сипаттамасының алмасуы жүреді.
Кітаптарда басқа қарапайым бейсызықты буындардың гармоникалық сызықтауының коэффициенттер кестесі көрсетілген.
Бұрын көрсетілгендей барлық циклдар автотербеліспен сәйкес келмейді, тек тұрақтылары тең. Нақты тапсырмадан автотербелістің болатыны немесе болмайтыны көрінеді. Бірақ, бұл сұрақты зерттеу қажет болады.
НӘ үшін Михайлов қисығын қолдануға болады:
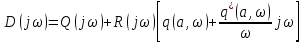(6.8)
Мұндағы –белгісі Михайлав қисығы бойымен өзгеретін ағымдағы ω параметрін гармоникалық сызықталу коэффициентіне кіретін жиіліктен ажырату үшін қойылған.
Әрбір а-ның нақты мәніне белгілі-бір Михайлов қисығы сәйкес келеді . а=апкезінде НӘ координат басы арқылы өтеді (6.2-сурет).
Қисықтың абсцисса осімен қиылысу нүктесінің маңайында интеграл шексіздікке ұмтылады. Шексіздікке баратын қисық астындағы ауданды жоспарлауды болдырмау үшін осы бөлімде уақытты есептеу кезінде орташа жылдамдық есептеледі.
-
Берілген дифференциалды теңдеу бойынша фазалық траекториялардың дифференциалды теңдеуі
Фазалық кеңістік түсінігі, фазалық траекториялар және олардың түрлері жоғарыда келтірілген. Бұл бөлімде сызықты емес автоматты басқару жүйелеріндегі процестердің кейбір маңызды ерекшеліктері қарапайым екінші ретті жүйелер үшін фазалық траекторияларды құру мысалдарымен суреттелетін болады.
Мысал 1. Өздігінен нивелирленбейтін объектісі бар және тұрақты жылдамдығы бар реттегіш жетекі бар автоматты басқару жүйесін алайық. Өздігінен нивелирленбеген реттелетін объектінің теңдеуі болады Массасы жоқ контроллер және қатты кері байланысы бар амортизатор үшін, яғни үшін біз аламыз
мұндағы - реттелетін шаманың салыстырмалы өзгерістері, сезімтал элементтің, реттеуші органның, кері байланыс элементінің және басқару золотникінің орын ауыстырулары (10.11, а-сурет), - коэффициент. Реттегіш жетегі екі нұсқада тұрақты жылдамдыққа ие болсын; 1) лезде ауысумен (16.22-сурет, ж) басқару элементі (золотник, ағынды түтік) өлі аймақпен бейтарап күйден өткенде (16.22-сурет, h) золотниктің «қабаттасуының» болуына байланысты немесе реактивті түтік. Бірінші жағдайда реттегіш жетектің теңдеуі болады.-
Берілген дифференциалды теңдеуі бойынша изоклин әдісімен фазалық траекторияны тұрғызу
Фазалық траекторияларын салу
х-y фазалық жазықтықта фазалық траектория сызғанда оны салудың келесі жалпы ережелерін назарға алған дұрыс.
-
Фазалық жазықтықта y=0 мәнінде, өзгеру жылдамдығы нөлге тең. -
y –тің оң кезінде, яғни фазалық жазықтықтың жоғарғы жағында бейнелеуші нүкте сНӘдан оңға қарай жылжиды, ал y -тің теріс мәнінде, яғни фазалық жылдамдықтың төмен жағында керісінше оңнан сНӘға қарай жылжиды. -
фазалық траекториялар өзара бір-бірімен қиылыспайды. Тек айрықша өрнектерде қиылысуы мүмкін.
Фазалық траекториялар y=f(x) фазалық теңдеуі бойынша салынады, оны табудың алдында ең алдымен жүйенің бастапқы дифференциалды теңдеулерінен фазалық траекториясының дифференциалды теңдеуін аламыз.
(2.2)Бірінші теңдеуді екінші теңдеуге бөле отырып уақыттан арыламыз
(2.3)Кейбір жағдайларда бұл теңдеу интегралданып, фазалық траекторияның теңдеуі
болып табылады, алынған теңдеу бойынша жүйенің фазалық портреті тұрғызылады.Қисық-сызықты сипаттамалары бар буындардан тұратын жүйелер үшін, фазалық жазықтықта (2.3) теңдеуінің сондай немесе басқа түрі кездесетін аймақтар белгіленуі мүмкін. Бұл аймақтар ауысып қосу сызықтары деген сызықтармен шектеледі (2.15-сурет).
2.15-сурет. Ауысып қосу сызықтарының қарапайым орналасу жағдайлары
(2.3) теңдеуі интегралданбаған жағдайда фазалық траектория салудың жуықталған әдісі бойынша тұрғызылады. Оны изокин әдісі деп атайды.
-
Берілген фазалық траектория бойынша өтпелі кезеңнің қисығын тұрғызу
Ляпунов функцисының оң анықталған түрін аламыз:
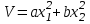(3.9) мұндағы a,b – кез-келген берілген оң сандар.
V шамасына өспелі тұрақты мәндер береміз: V= 0,C1,C2 … Олар төменгі теңдеулерге сәйкес келеді.
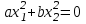
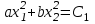
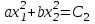(3.10)…………….
Бұл теңдеулердің біріншісі
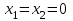нүктесіне сәйкес келеді, яғни координат басына, ал қалғандары фазалық кеңістіктегі белгілі бір қисыққа сәйкес келеді (3.2-сурет). 3.2-сурет. Фазалық кеңістік
Егер
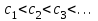болса, онда әрбір тұйық қисық ішінде координат бас нүктесін және кіші 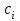-ге сәйкес келетін қисықтар болады. 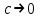болғанда қисықтар координат басына тартылады, яғни 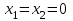нүктесінде ұмтылады. М бейнелеуші нүктенің барлық мүмкін болатын траекториясындағы қозғалысы V функциясының
үлкен мәніне сәйкес қисығынан V функциясының кіші мәніне сейкес қисығына өтетіні бізге белгілі болсын делік.-
Берілген бейсызықты жүйе үшін Ляпунов функциясын таңдап алып, жүйенің орнықтылығын зерттеу
мысалда Ляпунов теоремаларының дұрыстығын тексерелік.
Екінші ретті жүйені алайық (n=2)
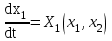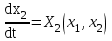
(3.8) Ляпунов функцисының оң анықталған түрін аламыз:
(3.9) мұндағы a,b – кез-келген берілген оң сандар.
V шамасына өспелі тұрақты мәндер береміз: V= 0,C1,C2 … Олар төменгі теңдеулерге сәйкес келеді.
(3.10)…………….
Бұл теңдеулердің біріншісі
нүктесіне сәйкес келеді, яғни координат басына, ал қалғандары фазалық кеңістіктегі белгілі бір қисыққа сәйкес келеді (3.2-сурет). 3.2-сурет. Фазалық кеңістік
Егер
болса, онда әрбір тұйық қисық ішінде координат бас нүктесін және кіші -ге сәйкес келетін қисықтар болады. болғанда қисықтар координат басына тартылады, яғни нүктесінде ұмтылады. М бейнелеуші нүктенің барлық мүмкін болатын траекториясындағы қозғалысы V функциясының үлкен мәніне сәйкес қисығынан V функциясының кіші мәніне сейкес қисығына өтетіні бізге белгілі болсын делік.-
Белгілі бір бейсызықтылықтың түріне жататын берілген АБЖ абсолютті орнықтылығын зерттеу
АБЖ-да сызықты емес тәуелділіктердің бар болуы жүйенің жағдайы сызықты емес дифференциалды теңдеулермен сипатталуына әкеліп соғады. Сызықты емес теңдеулердің көптеген топтары жалпы жағдайда шешілмейтіні белгілі, шешімдердің тек жеке жағдайлары жайында айтуға болады. Сондықтан сызықты емес жүйелерді зерттеуде әр түрлі жуықталған әдістер үлкен рНӘь атқарады.
Сызықты емес жүйелердің зерттеуді жуықталған әдістер арқылы жүйенің барлық динамикалық қасиеттері жайында қажетті толық мәліметтер ала алмаймыз, бірақ Олардың көмегімен арнайы қажетті сұрақтарға жауап берілуі мүмкін, мысалы, орнықтылығы, автотербелістің бар болуы, кез келген жеке режимдер сипаттамалары және тағы басқа.
Бірақ релелі типті жүйелерді (сипаттамалары тек горизонтальді немесе тек вертикальді түзулерден тұратын) сызықты дифференциалды теңдеулер аппараттық қолдану арқылы толық зерттеуге мүмкіндік береді.
Қазіргі кезде сызықты емес жүйелерді зерттеудің түрлі аналитикалық немесе графо-аналитикалық әдістері бар. Олардың ішінде орнықтылықты зерттеудің әдістері көзделген. Оларды екі үлкен топқа бөлген ыңғайлы: нақты және жуықталған.
-
Берілген қалыпты релелі элементтің гармоникалық сызықтау коэффициенттерін есептеу
Релелі элементтердің гармоникалық сызықтау коэффициенттері
(5.10) теңдеуінен q(a) және q/ (a) коэффициенттерін табамыз, кейбір типтік элементтер үшін (5.11) формула бойынша анықтаймыз:
5.3-сурет. Релелі элементтерінің сипаттамасы
БЭ жалпы сипаттама түрін (5.3,а-сурет) аламыз, мұнда m
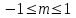интегралдағы бөлшек сан.Егер
кіріс шамасының тербелісінің a.
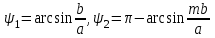(5.13)Бірнеше көмекші теңдеулер аламыз:
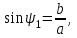
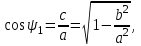
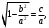
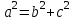
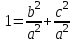
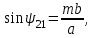
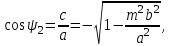
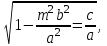
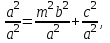
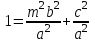
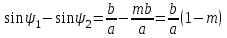
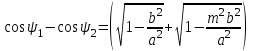
(5.11) интегралында симметриялық сипаттама үшін келесі түрдегі вектормен алуға болады:
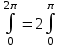
Олардың әрқайсысы үш қосындыға бөлінеді:
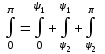
Бірінші және үшінші қосылғыш (5.3а және б-сурет) 0-ге тең болады. Онда (5.10) теңдеуі келесі түрде болады:
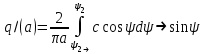
Немесе интегралдап, мынаны аламыз:
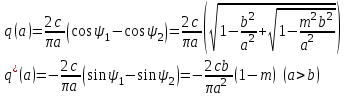(5.14)Гистеризисті емес түйін сипаттамасымен релелі буын үшін, мұнда (5.14) формуладан т=1болады деп есептеп алатынымыз(5.4-сурет).
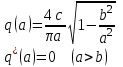
5.4-сурет. Үш позициялы реле
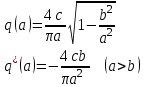(5.15) 5.5-сурет. Гистеризисі бар реле
Релелі буын үшін b=0 деп есептеп:
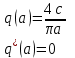(5.16) 5.6-сурет. Релелі буын
Соңғы мысалдан релелі сипаттаманың гармоникалық сызықтауының мағынасын көруге болдаы. Бұдан a берілген амплитуда мен қиылысатын MN тік сызықты ABCD сынық бөлігін шамамен алмастырып сипаттамасының алмасуы жүреді.
Кітаптарда басқа қарапайым бейсызықты буындардың гармоникалық сызықтауының коэффициенттер кестесі көрсетілген.
-
Бейсызықты жүйенің берілген годографы бойынша периодты режимнің орнықтылығын анықтау және егер автотербеліс бар болса оның параметрлерін анықтау
Бұрын көрсетілгендей барлық циклдар автотербеліспен сәйкес келмейді, тек тұрақтылары тең. Нақты тапсырмадан автотербелістің болатыны немесе болмайтыны көрінеді. Бірақ, бұл сұрақты зерттеу қажет болады.
НӘ үшін Михайлов қисығын қолдануға болады:
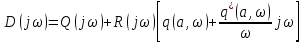(6.8)Мұндағы –белгісі Михайлав қисығы бойымен өзгеретін ағымдағы ω параметрін гармоникалық сызықталу коэффициентіне кіретін жиіліктен ажырату үшін қойылған.
Әрбір а-ның нақты мәніне белгілі-бір Михайлов қисығы сәйкес келеді . а=апкезінде НӘ координат басы арқылы өтеді (6.2-сурет).