Следующими клетками с минимальным значением тарифа являются клетки (4, 1) и (3, 3), в которых с₄₁ = с₃₃ = 5. В клетку (4, 1) можно разместить поставку min (1, 14) = 1, в клетку (3, 3) – поставку min (20, 15) = 15. Максимальным среди них является значение 15. Следовательно, х₃₃ = 15. Потребность третьего поставщика обнуляется, а в остальных клетках третьего столбца проставляется прочерк. У третьего поставщика остается еще пять единиц груза (20 – 15 = 5), которые подлежат дальнейшему распределению. Поскольку клетка (4, 1) не занята, то в нее можно разместить оставшуюся единицу груза, следовательно, х₄₁ = 1. При этом запас четвертого поставщика обнуляется, а в оставшуюся незанятой клетку четвертой строки (4, 2) вносится прочерк. Потребность первого потребителя сокращается до 14 (14 = 15 – 1):

bj ai		1	2	3	4
		15/14	16/	15/0	20/0
1	14/	6	10	7 -	5 -
2	11/	10	7	6 -	9 -
3	20/5/	13	14	5 15	7 -
4	21/1/0	5 1	10 -	6 -	4 20

Среди незанятых клеток минимальный тариф имеет клетка (1, 1): с₁₁ = 6. Объем возможной поставки определяется как min (14, 14) = 14. Следовательно, х₁₁ = 14. При этом обнуляется запас первого поставщика и потребность первого потребителя, а в свободных клетках первого столбца и первой строки ставится прочерк:

bj ai		1	2	3	4
		15/14/0	16/	15/0	20/0
1	14/0	6 14	10 -	7 -	5 -
2	11/	10 -	7	6 -	9 -
3	20/5/	13 -	14	5 15	7 -
4	21/1/0	5 1	10 -	6 -	4 20

---

Следующая клетка с минимальным тарифом – клетка (2, 2): с₂₂ = 7. Объем возможной поставки определяется как min (11, 16) = 11. Следовательно, х₂₂ = 11. При этом обнуляется запас второго поставщика. В последнюю свободную клетку (3, 2) вносится последняя поставка х₃₂ = 5:

bj ai		1	2	3	4
		15/14/0	16/5/0	15/0	20/0
1	14/0	6 14	10 -	7 -	5 -
2	11/0	10 -	7 11	6 -	9 -
3	20/5/0	13 -	14 5	5 15	7 -
4	21/1/0	5 1	10 -	6 -	4 20

Таким образом, все поставки распределены, получено начальное решение транспортной задачи:

.

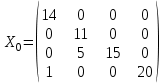Значение целевой функции:

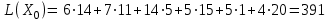ден. ед.

---

4. Решение транспортной задачи методом потенциалов

Метод потенциалов решения транспортной задачи для каждого получаемого решения Х_k включает выполнение следующих действий:

1. проверку решения на не вырожденность;

2. проверку решения на оптимальность, в т.ч.:

2.1. расчет потенциалов на основе известных тарифов для занятых клеток;

2.2. расчет оценок свободных клеток;

2.3. проверку условия оптимальности решения.

Проверка решения Х₀ на не вырожденность. Условие не вырожденности решения транспортной задачи: количество ненулевых элементов в решении транспортной задачи равно рангу матрицы.

Если количество ненулевых элементов в решении транспортной задачи (равно 6), меньшеN, а N = m + n – 1 = 4 + 4 – 1= 7, то решение вырожденное. Поскольку 6 < 7, то решение вырождено.

Проверка решения Х₀ на оптимальность.

Проверка решения транспортной задачи на оптимальность

Найденное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система m + n действительных чисел u_i и v_j, удовлетворяющих условиям u_i + v_j = c_ij для занятых клеток и u_i + v_j – c_ij  0 для свободных клеток.

Числа u_i и v_j называют потенциалами. В распределительную таблицу добавляют строку v_j и столбец u_i.

Потенциалы u_i и v_j находят из равенства u_i + v_j = c_ij, справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например, u₁ = 0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал u_i, то v_j = c_ij  u_i, если известен потенциал v_j, то u_i, = c_ij  v_j.

Величина _ij = u_i + v_j  c_ij называется оценкой свободных клеток. Если все оценки свободных клеток _ij 0, то опорное решение является оптимальным. Если хотя бы одна из оценок 

---

_ij ≥ 0, то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.

Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец u_i и строку v_j: Полагаем u₁ = 0, запишем это значение в последнем столбце первой строки таблицы.

Рассмотрим занятую клетку первой строки, которая расположена в первом столбце (1, 1), для нее выполняется условие u₁ + v₁= c₁₁. Откуда v₁ = c₁₁ – u₁ = 6 – 0 = 6, это значение запишем в последней строке таблицы:

bj ai		1	2	3	4	ui
		15	16	15	20
1	14	6 14	10 -	7 -	5 -	0
2	11	10 -	7 11	6 -	9 -
3	20	13 -	14 5	5 15	7 -
4	21	5 1	10 -	6 -	4 20
vj		6

Далее рассматривают ту из занятых клеток таблицы, для которых один из потенциалов известен.

Рассмотрим занятую клетку (4, 1): u₄ + v₁ = c₄₁, откуда u₄ = c₄₁ – v₁ = 5 – 6 = 1:

bj ai		1	2	3	4	ui
		15	16	15	20
1	14	6 14	10 -	7 -	5 -	0
2	11	10 -	7 11	6 -	9 -
3	20	13 -	14 5	5 15	7 -
4	21	5 1	10 -	6 -	4 20	1
vj		6

---

Для клетки (4, 4): u₄ + v₄ = c₄₄, откуда v₄ = c₄₄ – u₄ = 4 – (–1) = 5:

bj ai		1	2	3	4	ui
		15	16	15	20
1	14	6 14	10 -	7 -	5 -	0
2	11	10 -	7 11	6 -	9 -
3	20	13 -	14 5	5 15	7 -
4	21	5 1	10 -	6 -	4 20	1
vj		6			5

На данном этапе возникла ситуация, когда для оставшихся занятых клеток не известно ни одного из потенциалов. Это результат вырожденности решения. Для его преодоления в одну из клеток нужно внести нулевую поставку, таким образом, такая клетка станет условно занятой.

Методика преодоления вырожденности решения

Для преодоления вырожденности решения в одну из клеток нужно внести нулевую поставку. Нуль помещают в такую клетку, чтобы в каждой строке и столбце было не менее одной занятой клетки, и для данной клетки был известен один из потенциалов. Такая клетка становится условно занятой, она должна иметь наименьший тариф по сравнению с другими клетками, которые могут быть условно занятыми.
Рассмотрим, в какие клетки можно разместить нулевую поставку. Для неизвестного потенциала u₂ нулевую поставку можно разместить в клетках (2, 1) и (2, 4), для которых известны потенциалы

---

Смотрите также файлы

• Повышение конкурентоспособности организации на рынке гигиенических продуктов (на примере ооо Эссити).pdf

• Практических заданий по дисциплине жанры мультимедиа.docx

• Задачи представленной работы, способствующие достижению цели.docx

• 1. Данные, определенным образом организованные, имеющие смысл, значение и ценность для своего потребителя и необходимые для принятия им решений, а также реализации других функций и действий, это .docx

• Частное профессиональное образовательное учреждение Гуманитарный колледж Эдельвейс задание.docx