.
Решение:







1-19. На пути света поставлена стеклянная пластина толщиной d = 1 мм так, что угол падения луча равен 30. На сколько изменится оптическая длина пути луча?
Решение:

1-20. На мыльную плёнку с показателем преломления n = 1,33 падает нормально монохроматический свет с длиной волны = 0,6 мкм. Отражённый свет в результате интерференции имеет наибольшую яркость. Определить наименьшую толщину плёнки.
Решение: Наименьшая толщина плёнки будет равна половине длины волны в среде плёнки, умноженной на коэффициент преломления: t = λ/(2n) = 0,6 мкм/(2*1,33) ≈ 0,225 мкм. Ответ: наименьшая толщина плёнки равна примерно 0,225 мкм.

1-21. Радиус второго тёмного кольца Ньютона в отражённом свете r = 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны = 0,64 мкм.
Решение: Для решения этой задачи необходимо использовать формулу для радиуса n-ого тёмного кольца в отражённом свете: r_n = √(n * λ * f), где λ - длина волны света, f - фокусное расстояние линзы.
Мы знаем радиус второго тёмного кольца в отражённом свете r = 0,4 мм и длину волны света λ = 0,64 мкм. Для определения радиуса кривизны линзы необходимо найти фокусное расстояние f.
Для второго тёмного кольца n=2, поэтому: r_2 = √(2 * λ * f), f = r_2^2 / (2 * λ) = 0,4^2 / (2 * 0,64 * 10^-6) = 125000 мкм = 0,125 мм. Таким образом, радиус кривизны плосковыпуклой линзы равен 0,125 мм.

---

1-22. Плосковыпуклая стеклянная линза, радиус кривизны которой 12 см, прижата выпуклой стороной к стеклянной пластинке. Диаметры девятого и двенадцатого темных колец Ньютона в отражённом свете соответственно равны 0,9 мм и 1,2 мм. Определить длину волны падающего света.
Решение: Для определения длины волны падающего света можно использовать формулу для радиусов темных колец Ньютона: (1 уравнение), где r_n- радиус n-го кольца, λ - длина волны света, R- радиус кривизны линзы.
Из условия задачи известны диаметры девятого и двенадцатого темных колец Ньютона: (2 и 3 уравнение)
Радиусы этих колец можно найти, разделив диаметры на 2: (4 и 5 уравнение)



Подставляя значения радиусов и радиуса кривизны в формулу для r_n, получаем два уравнения: (6 и 7 уравнение)
Разделив второе уравнение на первое, получаем: (8, 9 и 10 уравнение)



где λ₁₂ и λ ₉- длины волн света, соответствующие двум кольцам.

Таким образом, отношение длин волн можно найти, возведя число 1.155 в квадрат: (11 и 12 уравнение)

Отсюда: (13 уравнение)

В оспользовавшись этим соотношением и известной длиной волны света, например, для жёлтого света, можно найти длину волны падающего света для данной задачи.

---

1-23. Ширина десяти колец Ньютона, отсчитываемых вдали от центра, составляет 0,8 мм. Ширина следующих 10 колец 0,5 мм. Определить радиус кривизны линзы, если наблюдение ведётся в отражённом свете. Длина волны падающего излучения 0,6 мкм.

---

Решение: Для решения задачи нам нужно использовать формулу для расчёта радиуса кривизны линзы в отражённом свете: (1 уравнение), где d- расстояние между колечками, λ - длина волны излучения.

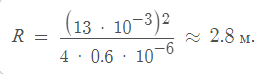Для первых 10 колец d = 0.8$ мм, для следующих 10 колец d = 0.5 мм. Всего мы имеем 20 колец, поэтому расстояние между первым и двадцатым кольцами будет: (2 уравнение)

Подставляя данную информацию в формулу, получим: (3 уравнение) Ответ: радиус кривизны линзы составляет около 2.8 м.

1-24. Интерференция световой волны длиной 0,6 мкм наблюдается в отражённом свете в тонком стеклянном клине. Показатель преломления стекла 1,5. Расстояние между соседними темными полосами 4 мм. Определить угол между гранями клина.
Решение: Используя формулу для расстояния между соседними максимумами интерференционной картины в тонком клине: d = λ / (n * sinθ), где d - расстояние между соседними максимумами, λ - длина волны света, n - показатель преломления стекла, θ - угол между гранями клина.
Подставляя известные значения, получаем: 4 мм = 0,6 мкм / (1,5 * sinθ), sinθ = 0,6 мкм / (1,5 * 4 мм) = 0,1, θ = arcsin(0,1) = 5,7°, Ответ: угол между гранями клина составляет 5,7°.

1-25. В опыте Юнга расстояние между отверстиями 0,2 см. Расстояние от отверстий до экрана 4 м, а от центрального до третьего интерференционного максимума 0,1 см. Определить: длину волны монохроматического света; расстояние между соседними интерференционными полосами. Какова будет картина интерференции, если щели освещать белым светом?
Решение: Длина волны света равна λ = (4 м × 0,1 см) / 0,2 см = 2 мм.
Расстояние между соседними интерференционными полосами равно δ = λD / d = (2 мм × 4 м) / 0,2 см = 4 мм.
Если освещать щели белым светом, то картина интерференции будет состоять из множества цветовых интерференционных полос, каждая со своей длиной волны. Расстояние между полосами будет меняться в зависимости от цвета света, так как для каждой длины волны δ будет разным.

---

1-26. Найти минимальную толщину плёнки с показателем преломления 1,34, при которой свет с длиной волны 0,6 мкм испытывает максимальное отражение, а свет с длиной волны 0,4 мкм не отражается. Угол падения света 30⁰.
Решение: Замена.

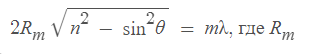
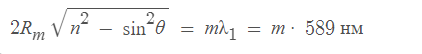1-27. Спектр натрия состоит из двух линий длиной 589 нм и 589,59 нм. Какое по счету тёмное кольцо Ньютона, соответствующее одной из этих линий, совпадает со следующим по счету темным кольцом, соответствующим другой линии, если наблюдение ведётся в отражённом свете?
Решение: Длина волны света, вызывающего m-ное (по счету) тёмное кольцо Ньютона, определяется из условия - радиус m-ного тёмного кольца 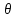, - угол падения света на пластину, n - показатель преломления стекла пластины, λ - длина волны света. При отражении света меняется только направление распространения, поэтому для отражённого света формула остаётся той же. (1 уравнение)

Подставим известные значения для двух длин волн и найдём, какому значению m соответствует каждое из них: (2 и 3 уравнение)

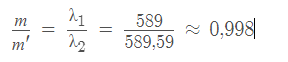Разделим уравнения и получим: (4 уравнение)

Следовательно, для того, чтобы тёмные кольца, соответствующие двум длинам волн, совпали, необходимо, чтобы m было на единицу меньше, чем m, то есть m = m - 1.

Ответ: тёмное кольцо, соответствующее длине волны 589,59 нм, совпадёт со следующим по счету кольцом, соответствующим длине волны 589 нм, если оно будет находиться на одну ступень ниже

---

Смотрите также файлы

• "Маркетинговая деятельность компании kfc".docx

• Бекітемін педагогика жне психология институтыны директоры Оразаева Г. С.docx

• Факторы конкурентоспособности Сильные стороны.docx

• Образ Каратаева в романе Л. Н. Толстого "Война и мир" Учитель использует технологию проблемного обучения. Организует условия, провоцирующие учебную деятельность ставит вопрос "Что может скрывать цитата.docx

• Шыыс азастан Облысы, Жарма ауданы, албатау ауылы Маяковский атындаы орта мектеп кмм сабаты зіндік талдау Сыныбы 7Б.docx