Файл: Решение Для определения расстояния между минимумами в эксперименте Юнга можно использовать формулу d sin m, где d расстояние между отверстиями, длина волны света,.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 1563
Скачиваний: 77
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Диаметр освещаемой поверхности можно определить как: Dp = 2 * r * tg(θ/2), где r - расстояние до Луны (примерно равно 384 400 км).
Подставляя значения, получим: Dp = 2 * 384 400 км * tg(7.66 * 10^-4 рад / 2) ≈ 4.2 км.
Таким образом, диаметр освещаемой на Луне поверхности составляет примерно 4.2 км.
1-44. Свет с длиной волны 589 нм падает нормально на дифракционную решётку с периодом 2,5 мкм, содержащую 10000 штрихов. Найти угловую ширину дифракционного максимума второго порядка.
Решение:
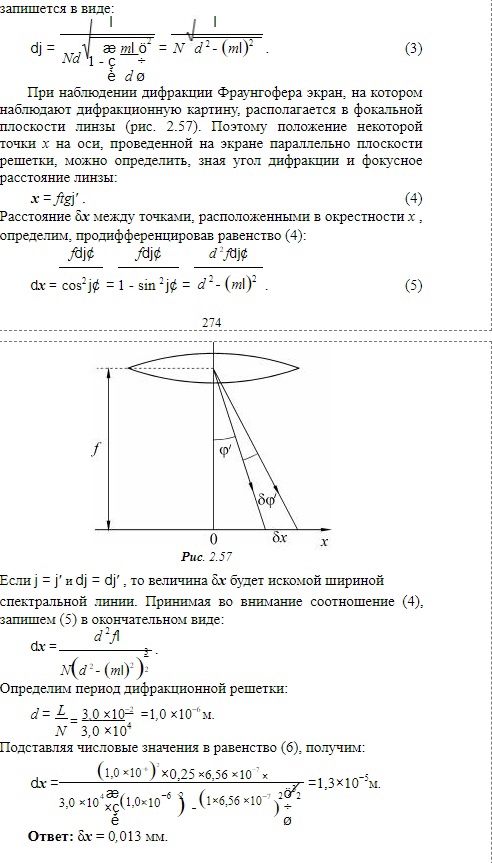
1-45. Определить ширину спектральной линии водорода, длина волны которой 0,656 мкм в спектре первого порядка, даваемого решёткой длиной 4 см. Фокусное расстояние линзы, проецирующей спектр на экран, равняется 20 см. Ширина спектральной линии – это расстояние между двумя минимумами, лежащими рядом с этой линией.Решение: Замена.
1-46. Сравнить разрешающие способности двух дифракционных решёток, если одна из них имеет 420 штрихов на 1 мм при ширине 2 см, а вторая содержит 720 штрихов на 1 мм при ширине решётки 4,8 см.
Решение: Разрешающая способность дифракционной решётки определяется формулой: d*sin(θ) = m*λ, где d - расстояние между штрихами, θ - угол дифракции, m - порядок дифракционного максимума, λ - длина волны света.
Для решётки с 420 штрихами на 1 мм и шириной 2 см расстояние между штрихами можно вычислить: d = 1 / 420 мм/штрих = 2,38*10^-6 м/штрих. Ширина решётки в метрах: L = 2 см = 0,02 м.
Разрешающая способность для этой решётки будет максимальной при максимальном порядке дифракционного максимума m = 1, при этом угол дифракции можно оценить как: sin(θ) ≈ θ = λ/d = 500 нм / 2,38*10^-6 м/штрих = 0,21 рад. Ширина дифракционной картины: Δx ≈ L*θ = 0,02 м * 0,21 рад = 0,0042 м = 4,2 мм.
Для решётки с 720 штрихами на 1 мм и шириной 4,8 см расстояние между штрихами можно вычислить: d = 1 / 720 мм/штрих = 1,39*10^-6 м/штрих. Ширина решётки в метрах: L = 4,8 см = 0,048 м.
Разрешающая способность для этой решётки будет максимальной при максимальном порядке дифракционного максимума m = 1, при этом угол дифракции можно оценить как: sin(θ) ≈ θ = λ/d = 500 нм / 1,39*10^-6 м/штрих = 0,36 рад. Ширина дифракционной картины: Δx ≈ L*θ = 0,048 м * 0,36 рад = 0,017 м = 1,7 см.
Таким образом, разрешающая способность второй решётки выше, чем у первой, поскольку ширина дифракционной картины для второй решётки меньше.
1-47. Каково наименьшее значение диаметра телескопа, который может разрешить дифракционные изображения двух звёзд, если угловое расстояние между ними 2΄΄? Глаз наиболее чувствителен к длине волны 5500
.Решение: Минимальный диаметр телескопа, который может разрешить дифракционные изображения двух звёзд с угловым расстоянием 2" и длиной волны 5500 Å, можно вычислить с помощью формулы Рэлея: D = 1,22 λ / θ, где D - диаметр телескопа, λ - длина волны света, а θ - угловое расстояние между звёздами.
Подставляя значения, получаем: D = 1,22 * 5500 Å / 2" = 16 м.
Таким образом, минимальный диаметр телескопа составляет 16 метров.
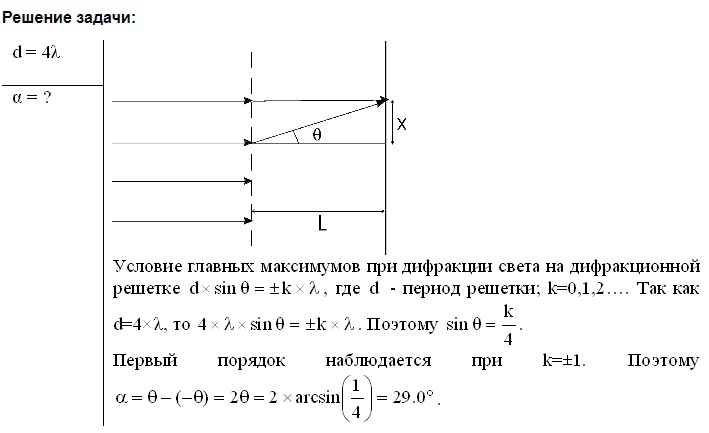
1-48. Постоянная дифракционной решётки в n = 4 раза больше длины световой волны монохроматического света, нормально падающего на её поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами. Решение:
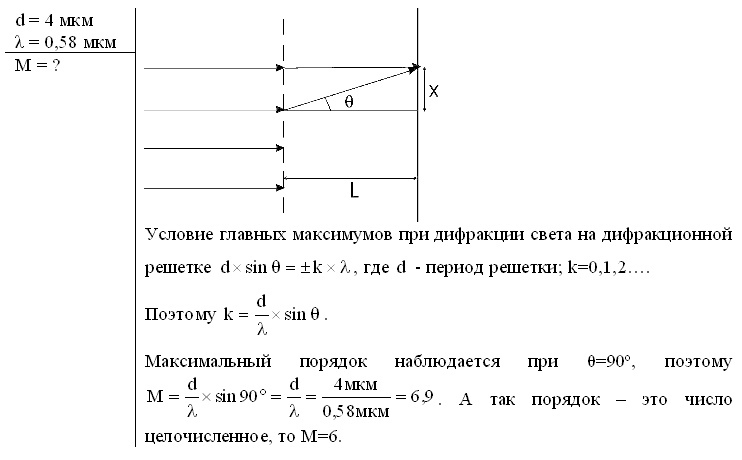
1-49. Расстояние между штрихами дифракционной решётки d = 4 мкм. На решётку падает нормально свет с длиной волны = 0,58 мкм. Максимум какого наибольшего порядка даёт эта решётка?Решение:
1-50. Какое наименьшее число штрихов должна содержать решётка, чтобы в спектре второго порядка можно было видеть раздельно две жёлтые линии натрия с длиной волны = 589,0 нм и = 589,6 нм? Какова длина l такой решётки, если расстояние между штрихами b = 5 мкм?Решение:
1-51. На поверхность дифракционной решётки нормально к её поверхности падает монохроматический свет. Постоянная дифракционной решётки в 4,6 раза больше длины световой волны. Найти общее число M дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.Решение:
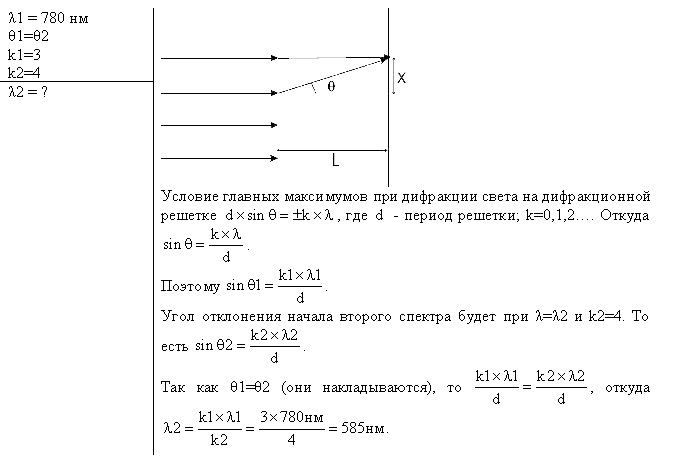
1-52. На дифракционную решётку падает нормально параллельный пучок лучей белого света. Спектры третьего и четвёртого порядков частично накладываются друг на друга. На какую длину волны в спектре четвёртого порядка накладывается граница ( = 780 нм) спектра третьего порядка?Решение:
1-53. На дифракционную решётку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проектируется помещённой вблизи решётки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра: = 780нм, =400 нм.Решение:
1-54. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей. Расстояние между атомными плоскостями кристалла d = 280 пм. Под углом = 65 к плоскости грани наблюдается дифракционный максимум первого порядка. Определить длину волны
рентгеновских лучей.Решение:
1-55. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна ( = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, равен 20. Определить ширину a щели.Решение:
1-56. На пластину со щелью, ширина которой а = 0,05 мм, падает нормально монохроматический свет с длиной волны = 0,7 мкм. Определить угол отклонения лучей, соответствующих первому дифракционному максимуму.
Решение: Угол отклонения лучей первого дифракционного максимума можно определить с помощью формулы: sin(φ) = λ / a, где λ - длина волны света, a - ширина щели.
Подставляя значения, получаем: sin(φ) = 0,7 мкм / 0,05 мм = 14
Ответ: угол отклонения лучей первого дифракционного максимума равен примерно 14 градусам.
1-57. Дифракционная решётка, освещённая нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол = 30. На какой угол отклоняет она спектр четвёртого порядка?
Решение: Для дифракционной решётки, отклоняющей спектр третьего порядка на угол φ = 30 градусов, угол отклонения спектра четвёртого порядка можно найти с помощью формулы: sin(θ4) = (4/3)sin(θ3), где θ4 - угол отклонения спектра четвёртого порядка, θ3 - угол отклонения спектра третьего порядка.
Подставив значения, получим: sin(θ4) = (4/3)sin(30 градусов) = 0.8, θ4 = sin^(-1)(0.8) = 53.1 градусов.
Таким образом, дифракционная решётка отклоняет спектр четвёртого порядка на угол 53.1 градусов.
1-58. При расширении круглого отверстия от одной до двух зон Френеля освещённость в центре экрана падает почти до нуля. Как согласовать этот факт с увеличением светового потока в два раза?
Решение: Увеличение светового потока в два раза может произойти при увеличении диаметра источника света в четыре раза. Однако при расширении круглого отверстия от одной до двух зон Френеля, световой поток не увеличивается в четыре раза, а распределяется по более широкой области, что приводит к уменьшению интенсивности света в центре экрана. Это объясняется интерференцией световых волн, создаваемых различными участками источника света, которые могут быть в фазе или противофазе в разных точках на экране.