Файл: Решение Для определения расстояния между минимумами в эксперименте Юнга можно использовать формулу d sin m, где d расстояние между отверстиями, длина волны света,.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 1560
Скачиваний: 77
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, то есть будет (m - 1)-м по счету.
1-28. На изображении натриевого пламени, длина волны которого 589 нм и наблюдаемого в вертикальной мыльной плёнке, видны тёмные горизонтальные полосы. Если глаз находится на уровне плёнки, то на высоте 4 см наблюдаются 8 полос. Определить угол между поверхностями плёнки, если показатель преломления мыльной воды 1,33.
Решение: Для определения угла между поверхностями мыльной плёнки можно использовать формулу для расстояния между соседними минимумами интерференционной картины, которую можно выразить как: d = λ/(2n sinθ), где λ - длина волны света, n - показатель преломления среды, θ - угол между поверхностями плёнки.
Расстояние между соседними минимумами можно выразить через высоту наблюдения и количество видимых минимумов: d = h/N, где h - высота наблюдения (4 см), N - количество видимых минимумов (8).
Сравнивая два выражения для d, получим: λ/(2n sinθ) = h/N
Отсюда можно выразить угол θ: θ = arcsin(λN / 2nh)
Подставляя известные значения, получаем: θ = arcsin(589 нм * 8 / (2 * 1,33 * 4 см)) ≈ 41,5°
Таким образом, угол между поверхностями мыльной плёнки составляет примерно 41,5 градусов.
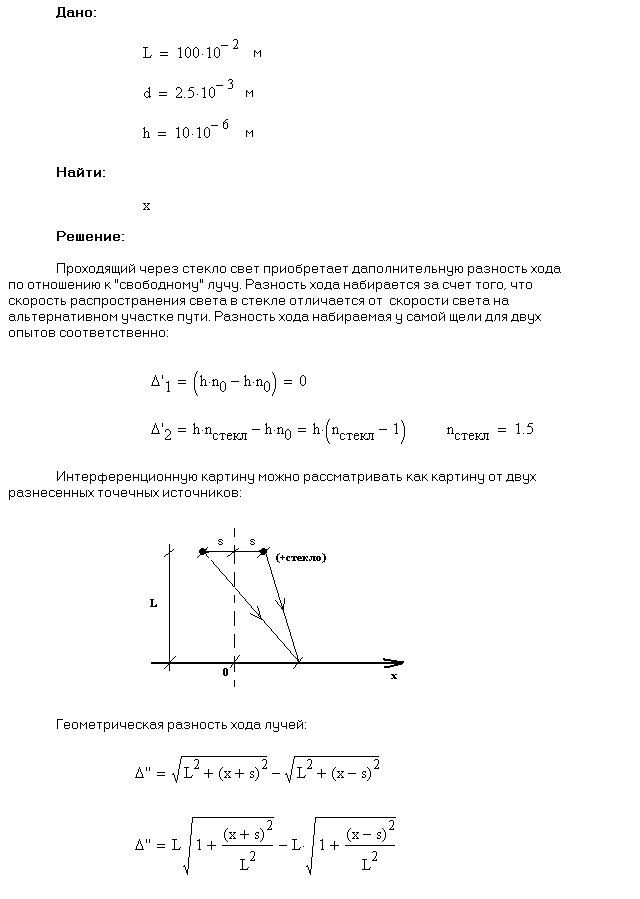
1-29. Плоская монохроматическая волна падает на диафрагму с двумя узкими щелями, расстояние между которыми 3 мм. На экране, который расположен на расстоянии 1 м от диафрагмы, наблюдают интерференционные полосы. На какое расстояние и в какую сторону сместятся полосы, если одну из щелей перекрыть стеклянной пластинкой 8 мкм?
Решение: Замена.
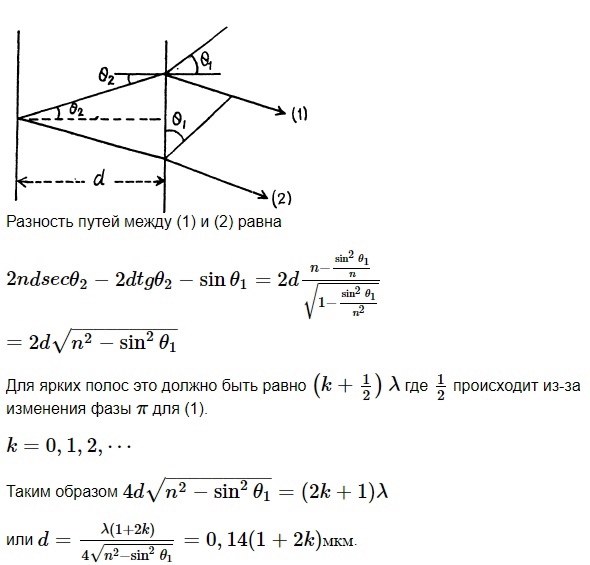
1-30. На тонкую плёнку воды под углом 300 падает параллельный пучок белого света. При какой толщине плёнки зеркально отражённый свет окрашен в жёлтый цвет (λ = 589 нм) максимально?
Решение: Замена.
1-31. Определить наименьшую толщину и показатель преломления плёнки, чтобы ею можно было просветить поверхность стекла для зеленного света с длиной волны 0,55 мкм, если показатель преломления стекла для этой длины волны 1,52. Решение: Нам необходимо найти толщину и показатель преломления плёнки, чтобы она пропускала зелёный свет с длиной волны 0,55 мкм и имела достаточно высокий коэффициент преломления, чтобы она могла использоваться для просветления поверхности стекла. Для этого мы можем воспользоваться формулой толщины плёнки: t = λ / (2 * n), где t - толщина плёнки, λ - длина волны света, n - показатель преломления плёнки. Мы знаем длину волны зелёного света λ = 0,55 мкм и показатель преломления стекла n = 1,52 для этой длины волны. Для того чтобы найти минимальную толщину плёнки, мы можем предположить, что она имеет такой же показатель преломления, как стекло (n = 1,52). Подставляя эти значения в формулу, получаем: t = 0,55 мкм / (2 * 1,52) = 0,18 мкм. Таким образом, наименьшая толщина плёнки должна быть примерно 0,18 мкм, а её показатель преломления должен быть не менее 1,52.
1-32. Плоская световая волна падает на бизеркала Френеля, угол между которыми = 2,0. Определить длину волны света, если ширина интерференционной полосы на экране х = 0,55 мм.
Решение:
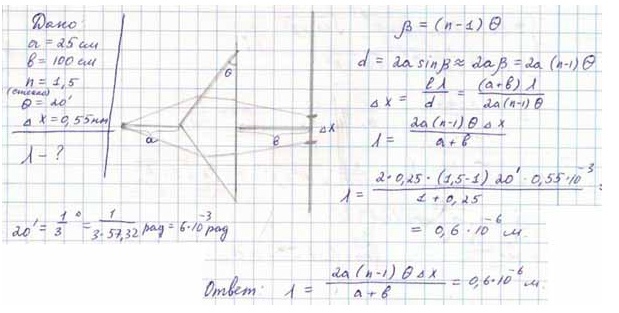
1-33. Расстояние от бипризмы Френеля до узкой щели и экрана равны соответственно а = 25 см и b = 100 см. Бипризма стеклянная с преломляющим углом = 20. Найти длину волны света, если ширина интерференционной полосы на экране х = 0,55 мм.
Решение:
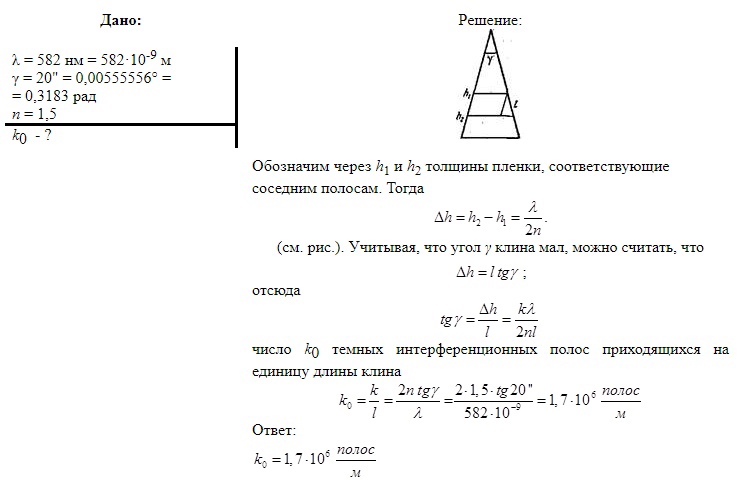
1-34. На стеклянный клин падает нормально пучок света с длиной волны 582 нм. Угол клина равен 20''. Какое число темных интерференционных полос приходится на единицу длины клина? Показатель преломления стекла 1,5.
Решение:
1-35. Плосковыпуклая стеклянная линза с радиусом кривизны сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отражённом свете равны d1 = 1,00 мм и
d2 = 1,50 мм. Определить длину волны света.
Решение:
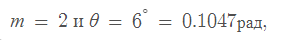
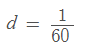
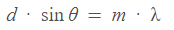1-36. На дифракционную решётку, имеющую 60 штрихов на миллиметр, падает нормально свет от натриевого пламени с длиной волны 589 нм. Определить длину волны, для которой угол отклонения во втором порядке равен 60, если в спектре третьего порядка первая длина волны отклоняется на 100.
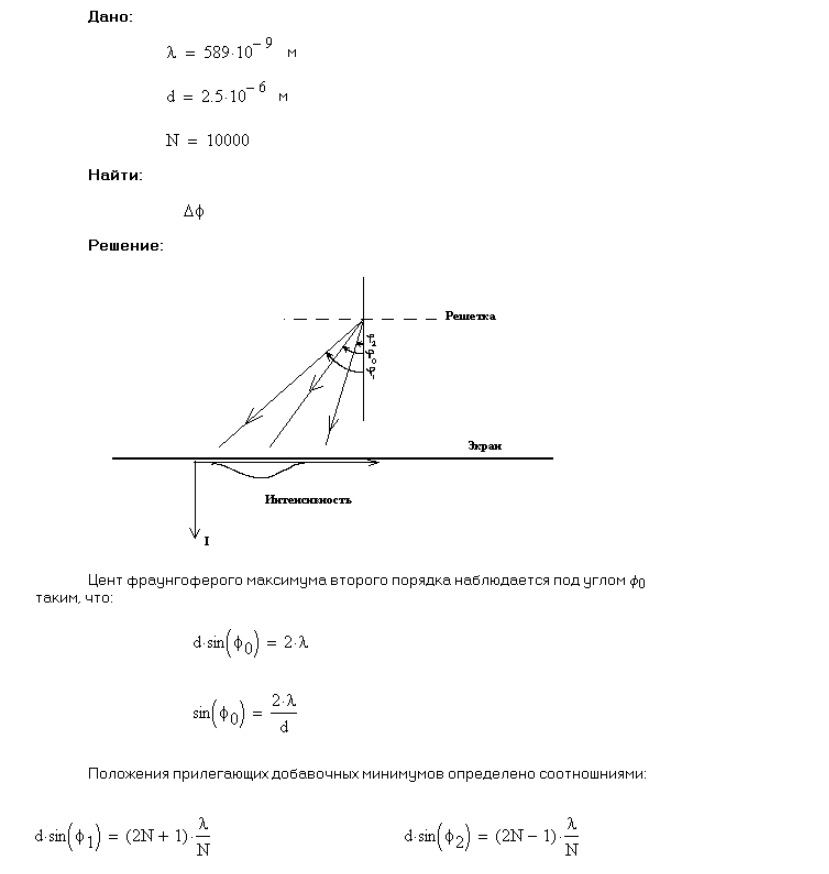
Решение: Для дифракционной решетки с шагом и длиной волны λ угол отклонения для m-го порядка дается формулой дифракционной решетки: (1 и 2 уравнение)
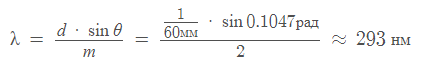Для второго порядка, поэтому: (3 уравнение)
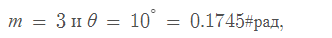
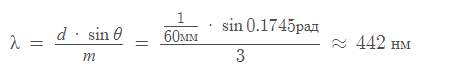
Для третьего порядка, поэтому
1-37. Определить длину дифракционной решётки, имеющую 500 штрихов на 1 мм, если в спектре второго порядка раздельно видны две линии натрия 5800 
и 5896 .
Решение: Замена.
1-38. Наименьший угол зрения, при котором глаз видит два штриха, равен 1΄. Определить наименьшее расстояние, которое различит глаз на расстоянии наилучшего зрения (25 см).
Решение: Наименьший угол разрешения (Δ) выражается формулой Δ = 1,22λ/D, где λ - длина волны света, а D - диаметр зрачка (обычно принимается равным 0,5 мм).
Для видимого света λ ≈ 0,0005 мм, поэтому Δ ≈ 2,4*10^-4 рад.
Наименьшее расстояние (d), различимое глазом, связано с углом Δ формулой d = 25*tan(Δ/2).
Подставляя значения, получаем: d ≈ 0,03 мм.
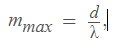
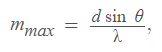1 -39. Определить наибольший порядок спектра, даваемый дифракционной решёткой, имеющей 600 штрихов на 1 мм в двух случаях: а) свет падает на решётку нормально; б) свет падает на решётку под углом 300. Длина волны света 580 мкм.
Решение: а) Наибольший порядок спектра, задаваемый дифракционной решёткой при нормальном падении света, определяется формулой: (1 уравнение), где d - расстояние между штрихами решётки, λ - длина волны света. Подставляя известные значения, получаем: (2 уравнение)
Таким образом, наибольший порядок спектра при нормальном падении света равен 2.
б) При падении света на решётку под углом максимальный порядок спектра вычисляется по формуле: (3 уравнение), г де d - расстояние между штрихами решётки, λ - длина волны света, - угол падения света на решётку. Подставляя известные значения, получаем: (4 уравнение)
Таким образом, наибольший порядок спектра при падении света на решётку под углом 30 градусов равен 1.
1-40. На дифракционную решётку, имеющую 100 штрихов на 1мм, нормально падает параллельный пучок белого света. Определить разность углов конца первого и начала второго спектра, если длины крайних красных и крайних фиолетовых волн равны соответственно 700 и 400 мкм.
Решение: Замена.
1-41. Определить длину волны монохроматического света, падающего нормально на решётку с периодом 2,6 мкм, если угол между максимумами первого и второго порядка равен 200. Определить угловое расстояние между главным максимумом и ближайшим к нему минимумом. Решётка имеет 500 штрихов на 1 мм.
Решение: Для нахождения длины волны λ воспользуемся формулой дифракции на решётке: d·sinθ = m·λ, где d - период решётки, θ - угол между лучом и нормалью к решётке, m - порядок максимума.
Для первого максимума (m = 1) получаем: λ = d·sinθ = 2,6·10^-6·sin20° ≈ 9,01·10^-7 м = 901 нм.
Для нахождения углового расстояния между главным максимумом и ближайшим к нему минимумом воспользуемся формулой: Δθ = λ/d, где λ - длина волны, d - период решётки.
Подставляем найденные значения: Δθ = λ/d = 9,01·10^-7/500 ≈ 1,80·10^-9 рад.
Ответ: длина волны монохроматического света ≈ 901 нм, угловое расстояние между главным максимумом и ближайшим к нему минимумом ≈ 1,80·10^-9 рад.
1-42. Свет с длиной волны 0,6 мкм падает нормально на дифракционную решётку. Два смежных главных максимумов получаются, если sin φ1 = 0,2 и sin φ2 = 0,3, а спектр четвёртого порядка отсутствует. Определить: 1) расстояние между соседними щелями; 2) наименьшую ширину отдельной щели; 3) максимальное число порядков в этих случаях.
Решение: 1) Расстояние между соседними щелями d можно вычислить по формуле d = λ / (sin φ2 - sin φ1), где λ - длина волны света. Подставляя значения sin φ1 = 0,2, sin φ2 = 0,3 и λ = 0,6 мкм, получаем d = 1,2 мкм.
2) Ширину отдельной щели можно вычислить по формуле b = λ / (m * sin φ), где m - порядок спектра, а φ - угол отклонения максимума. Так как спектр четвёртого порядка отсутствует, то максимальный порядок равен 3. Подставляя значения m = 1, sin φ = 0,2 и λ = 0,6 мкм, получаем b = 3 мкм.
3) Максимальное число порядков можно найти по формуле m_max = (d * sin φ_max) / λ, где φ_max - угол отклонения, при котором максимальный порядок спектра ещё виден. Так как максимальный порядок равен 3 и спектр четвёртого порядка отсутствует, то m_max = 3. Подставляя значения d = 1,2 мкм и λ = 0,6 мкм, получаем sin φ_max = m_max * λ / d = 1,5. Однако такой угол отклонения уже выходит за пределы главного максимума, поэтому максимальное число порядков в данном случае равно 3.
1-43. Лазерный пучок света диаметром 1 см и длиной волны 0,633 мкм, расходимость которого определяется только дифракцией, направлен на Луну. Определить диаметр освещаемой на Луне поверхности.
Решение: Диаметр освещаемой на Луне поверхности можно определить с помощью формулы дифракционной расходимости: θ = 1.22 * λ / D, где θ - угловой размер (в радианах) дифракционного пятна на Луне, λ - длина волны света, D - диаметр лазерного пучка.
Подставляя значения, получим: θ = 1.22 * 0.633 мкм / 1 см = 7.66 * 10^-4 рад.
1-28. На изображении натриевого пламени, длина волны которого 589 нм и наблюдаемого в вертикальной мыльной плёнке, видны тёмные горизонтальные полосы. Если глаз находится на уровне плёнки, то на высоте 4 см наблюдаются 8 полос. Определить угол между поверхностями плёнки, если показатель преломления мыльной воды 1,33.
Решение: Для определения угла между поверхностями мыльной плёнки можно использовать формулу для расстояния между соседними минимумами интерференционной картины, которую можно выразить как: d = λ/(2n sinθ), где λ - длина волны света, n - показатель преломления среды, θ - угол между поверхностями плёнки.
Расстояние между соседними минимумами можно выразить через высоту наблюдения и количество видимых минимумов: d = h/N, где h - высота наблюдения (4 см), N - количество видимых минимумов (8).
Сравнивая два выражения для d, получим: λ/(2n sinθ) = h/N
Отсюда можно выразить угол θ: θ = arcsin(λN / 2nh)
Подставляя известные значения, получаем: θ = arcsin(589 нм * 8 / (2 * 1,33 * 4 см)) ≈ 41,5°
Таким образом, угол между поверхностями мыльной плёнки составляет примерно 41,5 градусов.
1-29. Плоская монохроматическая волна падает на диафрагму с двумя узкими щелями, расстояние между которыми 3 мм. На экране, который расположен на расстоянии 1 м от диафрагмы, наблюдают интерференционные полосы. На какое расстояние и в какую сторону сместятся полосы, если одну из щелей перекрыть стеклянной пластинкой 8 мкм?Решение: Замена.
1-30. На тонкую плёнку воды под углом 300 падает параллельный пучок белого света. При какой толщине плёнки зеркально отражённый свет окрашен в жёлтый цвет (λ = 589 нм) максимально?Решение: Замена.
1-31. Определить наименьшую толщину и показатель преломления плёнки, чтобы ею можно было просветить поверхность стекла для зеленного света с длиной волны 0,55 мкм, если показатель преломления стекла для этой длины волны 1,52. Решение: Нам необходимо найти толщину и показатель преломления плёнки, чтобы она пропускала зелёный свет с длиной волны 0,55 мкм и имела достаточно высокий коэффициент преломления, чтобы она могла использоваться для просветления поверхности стекла. Для этого мы можем воспользоваться формулой толщины плёнки: t = λ / (2 * n), где t - толщина плёнки, λ - длина волны света, n - показатель преломления плёнки. Мы знаем длину волны зелёного света λ = 0,55 мкм и показатель преломления стекла n = 1,52 для этой длины волны. Для того чтобы найти минимальную толщину плёнки, мы можем предположить, что она имеет такой же показатель преломления, как стекло (n = 1,52). Подставляя эти значения в формулу, получаем: t = 0,55 мкм / (2 * 1,52) = 0,18 мкм. Таким образом, наименьшая толщина плёнки должна быть примерно 0,18 мкм, а её показатель преломления должен быть не менее 1,52.1-32. Плоская световая волна падает на бизеркала Френеля, угол между которыми = 2,0. Определить длину волны света, если ширина интерференционной полосы на экране х = 0,55 мм.
Решение:
1-33. Расстояние от бипризмы Френеля до узкой щели и экрана равны соответственно а = 25 см и b = 100 см. Бипризма стеклянная с преломляющим углом = 20. Найти длину волны света, если ширина интерференционной полосы на экране х = 0,55 мм.
Решение:
1-34. На стеклянный клин падает нормально пучок света с длиной волны 582 нм. Угол клина равен 20''. Какое число темных интерференционных полос приходится на единицу длины клина? Показатель преломления стекла 1,5.Решение:
1-35. Плосковыпуклая стеклянная линза с радиусом кривизны сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отражённом свете равны d1 = 1,00 мм и d2 = 1,50 мм. Определить длину волны света.
Решение:
1-36. На дифракционную решётку, имеющую 60 штрихов на миллиметр, падает нормально свет от натриевого пламени с длиной волны 589 нм. Определить длину волны, для которой угол отклонения во втором порядке равен 60, если в спектре третьего порядка первая длина волны отклоняется на 100.Решение: Для дифракционной решетки с шагом и длиной волны λ угол отклонения для m-го порядка дается формулой дифракционной решетки: (1 и 2 уравнение)
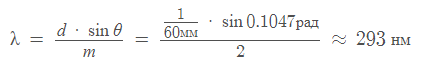Для второго порядка, поэтому: (3 уравнение)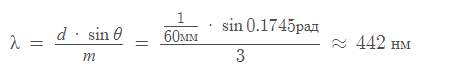 Для третьего порядка, поэтому
1-37. Определить длину дифракционной решётки, имеющую 500 штрихов на 1 мм, если в спектре второго порядка раздельно видны две линии натрия 5800 и 5896 .Решение: Замена.
1-38. Наименьший угол зрения, при котором глаз видит два штриха, равен 1΄. Определить наименьшее расстояние, которое различит глаз на расстоянии наилучшего зрения (25 см).
Решение: Наименьший угол разрешения (Δ) выражается формулой Δ = 1,22λ/D, где λ - длина волны света, а D - диаметр зрачка (обычно принимается равным 0,5 мм).
Для видимого света λ ≈ 0,0005 мм, поэтому Δ ≈ 2,4*10^-4 рад.
Наименьшее расстояние (d), различимое глазом, связано с углом Δ формулой d = 25*tan(Δ/2).
Подставляя значения, получаем: d ≈ 0,03 мм.
1 -39. Определить наибольший порядок спектра, даваемый дифракционной решёткой, имеющей 600 штрихов на 1 мм в двух случаях: а) свет падает на решётку нормально; б) свет падает на решётку под углом 300. Длина волны света 580 мкм.Решение: а) Наибольший порядок спектра, задаваемый дифракционной решёткой при нормальном падении света, определяется формулой: (1 уравнение), где d - расстояние между штрихами решётки, λ - длина волны света. Подставляя известные значения, получаем: (2 уравнение)
Таким образом, наибольший порядок спектра при нормальном падении света равен 2.
б) При падении света на решётку под углом максимальный порядок спектра вычисляется по формуле: (3 уравнение), г де d - расстояние между штрихами решётки, λ - длина волны света, - угол падения света на решётку. Подставляя известные значения, получаем: (4 уравнение)Таким образом, наибольший порядок спектра при падении света на решётку под углом 30 градусов равен 1.
1-40. На дифракционную решётку, имеющую 100 штрихов на 1мм, нормально падает параллельный пучок белого света. Определить разность углов конца первого и начала второго спектра, если длины крайних красных и крайних фиолетовых волн равны соответственно 700 и 400 мкм.Решение: Замена.
1-41. Определить длину волны монохроматического света, падающего нормально на решётку с периодом 2,6 мкм, если угол между максимумами первого и второго порядка равен 200. Определить угловое расстояние между главным максимумом и ближайшим к нему минимумом. Решётка имеет 500 штрихов на 1 мм.
Решение: Для нахождения длины волны λ воспользуемся формулой дифракции на решётке: d·sinθ = m·λ, где d - период решётки, θ - угол между лучом и нормалью к решётке, m - порядок максимума.
Для первого максимума (m = 1) получаем: λ = d·sinθ = 2,6·10^-6·sin20° ≈ 9,01·10^-7 м = 901 нм.
Для нахождения углового расстояния между главным максимумом и ближайшим к нему минимумом воспользуемся формулой: Δθ = λ/d, где λ - длина волны, d - период решётки.
Подставляем найденные значения: Δθ = λ/d = 9,01·10^-7/500 ≈ 1,80·10^-9 рад.
Ответ: длина волны монохроматического света ≈ 901 нм, угловое расстояние между главным максимумом и ближайшим к нему минимумом ≈ 1,80·10^-9 рад.
1-42. Свет с длиной волны 0,6 мкм падает нормально на дифракционную решётку. Два смежных главных максимумов получаются, если sin φ1 = 0,2 и sin φ2 = 0,3, а спектр четвёртого порядка отсутствует. Определить: 1) расстояние между соседними щелями; 2) наименьшую ширину отдельной щели; 3) максимальное число порядков в этих случаях.
Решение: 1) Расстояние между соседними щелями d можно вычислить по формуле d = λ / (sin φ2 - sin φ1), где λ - длина волны света. Подставляя значения sin φ1 = 0,2, sin φ2 = 0,3 и λ = 0,6 мкм, получаем d = 1,2 мкм.
2) Ширину отдельной щели можно вычислить по формуле b = λ / (m * sin φ), где m - порядок спектра, а φ - угол отклонения максимума. Так как спектр четвёртого порядка отсутствует, то максимальный порядок равен 3. Подставляя значения m = 1, sin φ = 0,2 и λ = 0,6 мкм, получаем b = 3 мкм.
3) Максимальное число порядков можно найти по формуле m_max = (d * sin φ_max) / λ, где φ_max - угол отклонения, при котором максимальный порядок спектра ещё виден. Так как максимальный порядок равен 3 и спектр четвёртого порядка отсутствует, то m_max = 3. Подставляя значения d = 1,2 мкм и λ = 0,6 мкм, получаем sin φ_max = m_max * λ / d = 1,5. Однако такой угол отклонения уже выходит за пределы главного максимума, поэтому максимальное число порядков в данном случае равно 3.
1-43. Лазерный пучок света диаметром 1 см и длиной волны 0,633 мкм, расходимость которого определяется только дифракцией, направлен на Луну. Определить диаметр освещаемой на Луне поверхности.Решение: Диаметр освещаемой на Луне поверхности можно определить с помощью формулы дифракционной расходимости: θ = 1.22 * λ / D, где θ - угловой размер (в радианах) дифракционного пятна на Луне, λ - длина волны света, D - диаметр лазерного пучка.
Подставляя значения, получим: θ = 1.22 * 0.633 мкм / 1 см = 7.66 * 10^-4 рад.