Файл: Сборник задач по высшей математике. РостовнаДону 2008г. 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 70
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§3. Функциональные ряды. Область сходимости функциональности ряда.
3.1 Основные определения.
Определение. Ряд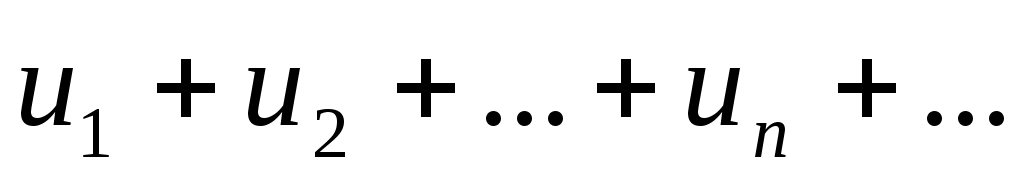 называется функциональным, если его члены являются функциями переменной
называется функциональным, если его члены являются функциями переменной 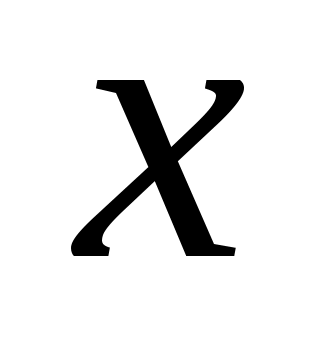 :
:
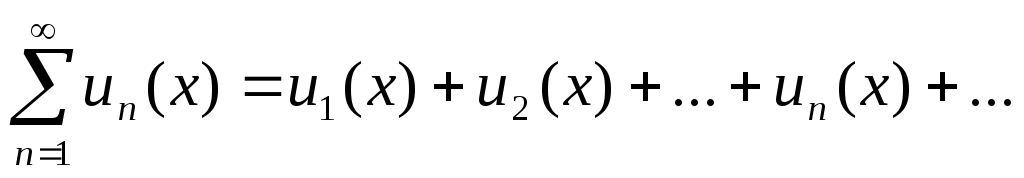
При различных значениях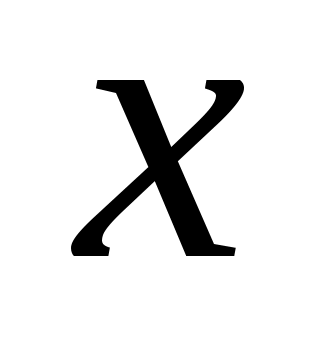 из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
Определение. Совокупность значений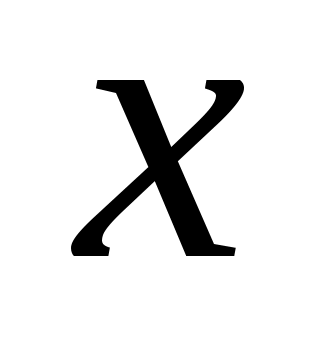 , при которых функциональный ряд сходится, называется областью его сходимости.
, при которых функциональный ряд сходится, называется областью его сходимости.
В области сходимости ряда его сумма является некоторой функцией от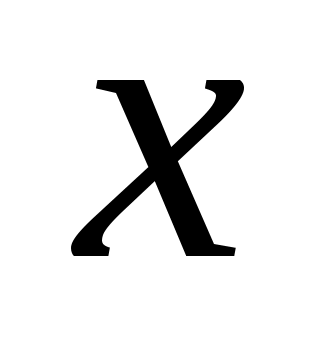 , поэтому сумму функционального ряда обозначают
, поэтому сумму функционального ряда обозначают 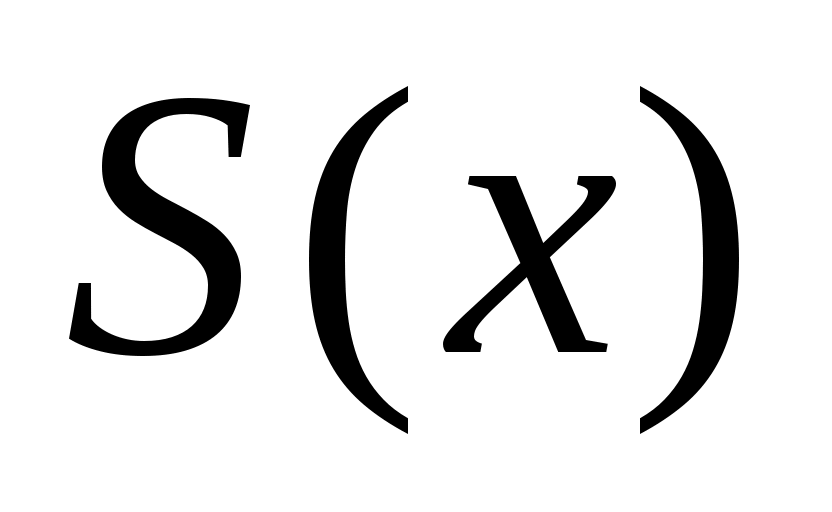 .
.
Пример. Функциональный ряд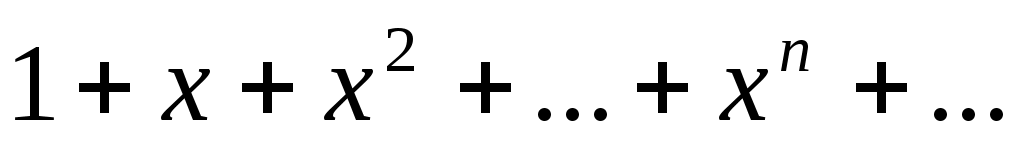 сходится при всех
сходится при всех 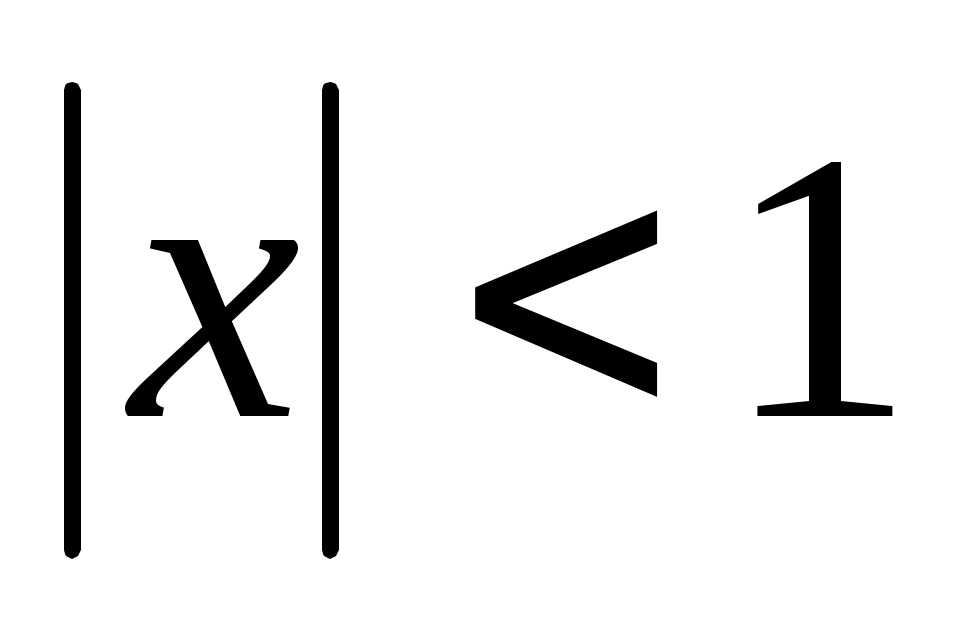 , т.е. в интервале (-1;1), т.к. при любом
, т.е. в интервале (-1;1), т.к. при любом 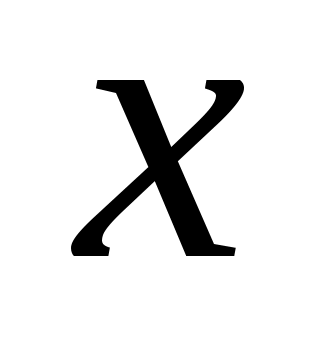 из этого интервала соответствующий числовой ряд представляет собой бесконечно убывающую геометрическую прогрессию.
из этого интервала соответствующий числовой ряд представляет собой бесконечно убывающую геометрическую прогрессию.
В интервале сходимости сумма ряда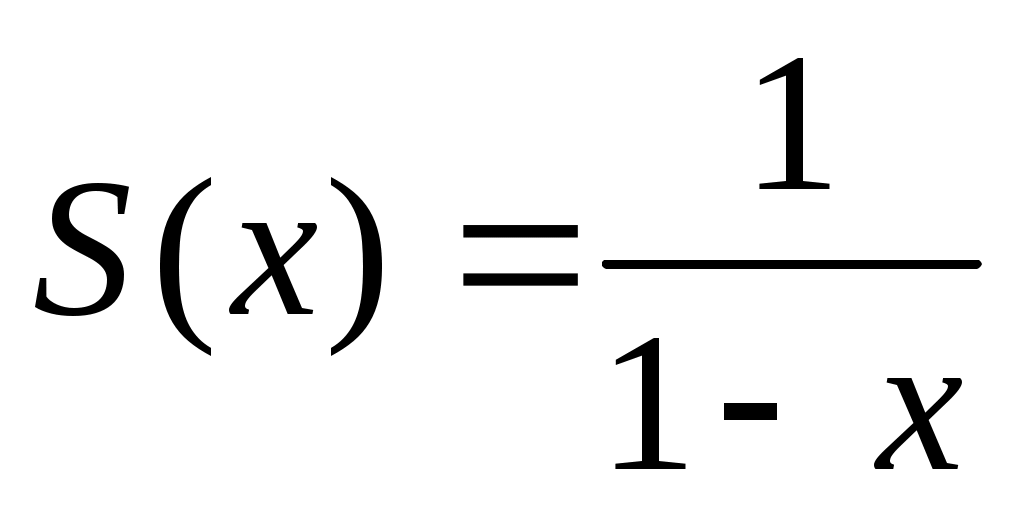
При всех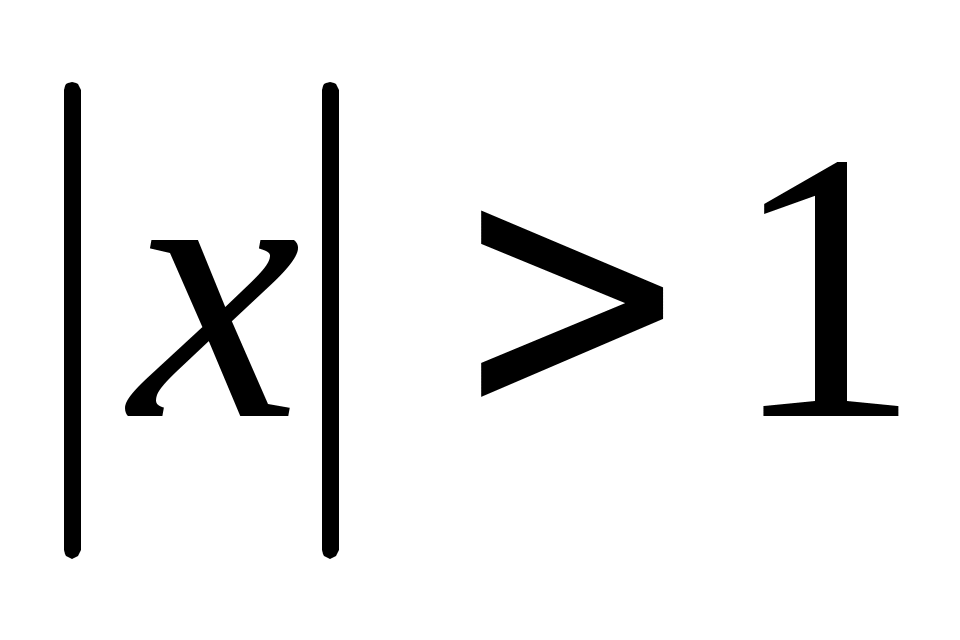 этот ряд расходится.
этот ряд расходится.
Обозначим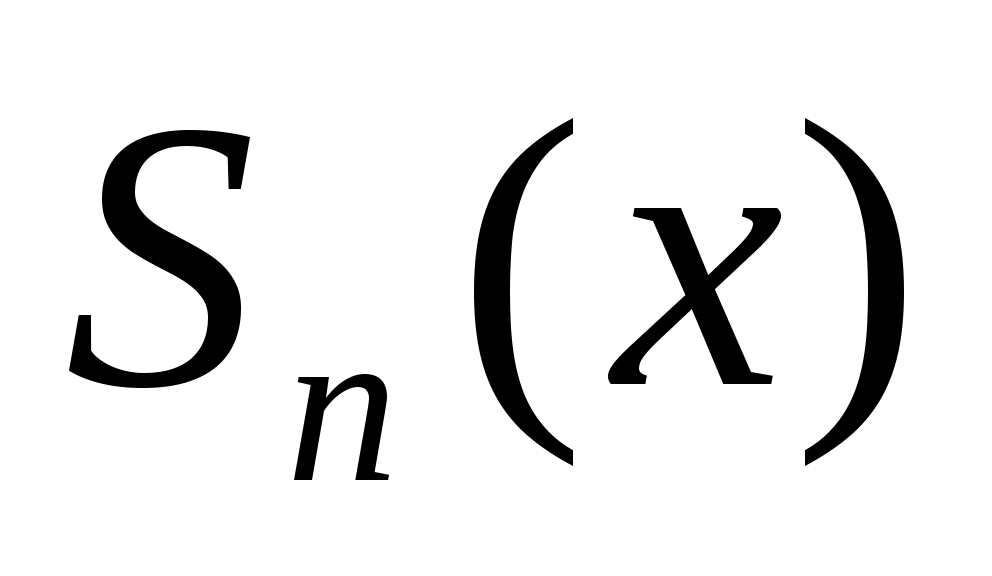 сумму первых
сумму первых 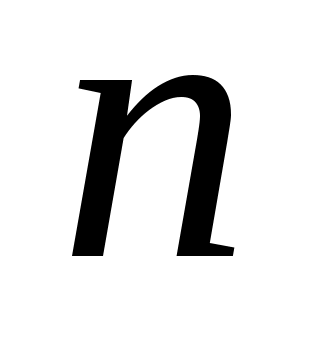 членов ряда. Если ряд сходится и сумма его
членов ряда. Если ряд сходится и сумма его 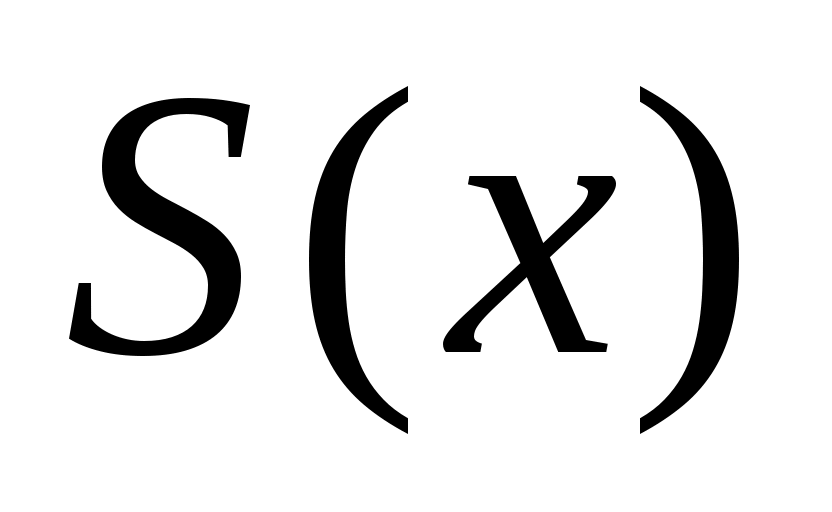 , то
, то
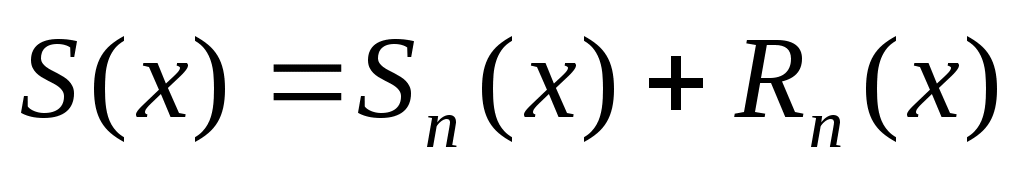 ,
,
где
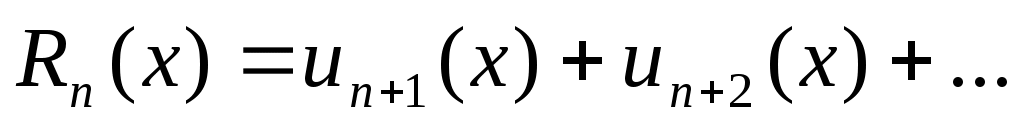
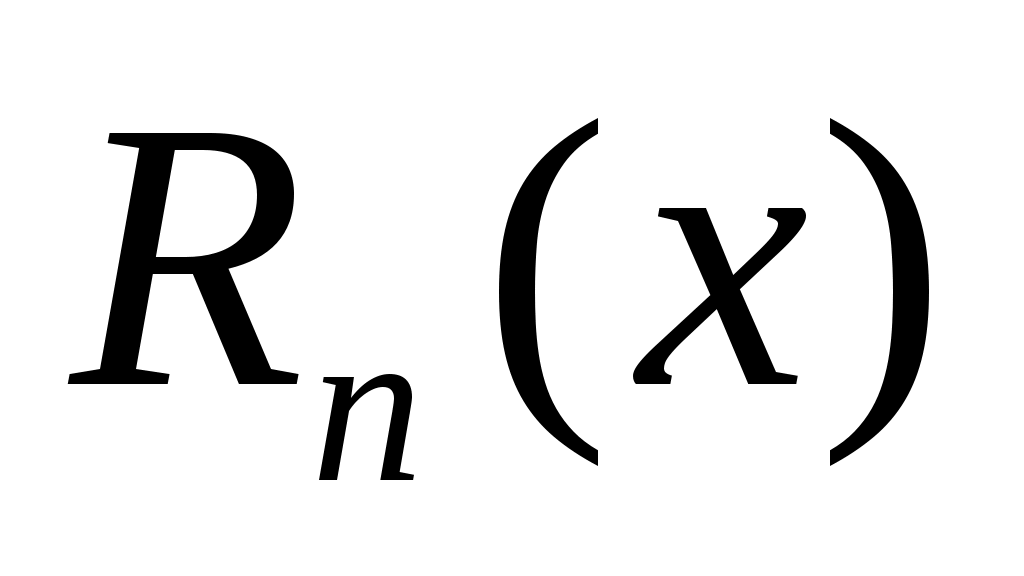 называется остатком ряда. Для всех
называется остатком ряда. Для всех  в области сходимости
в области сходимости
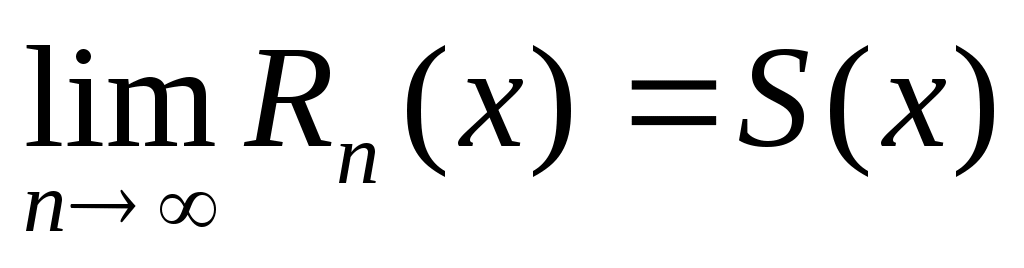 ,
,
Поэтому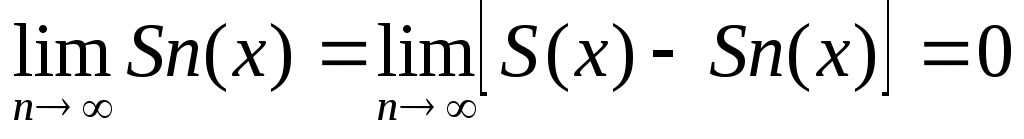 ,
,
Т.е. остаток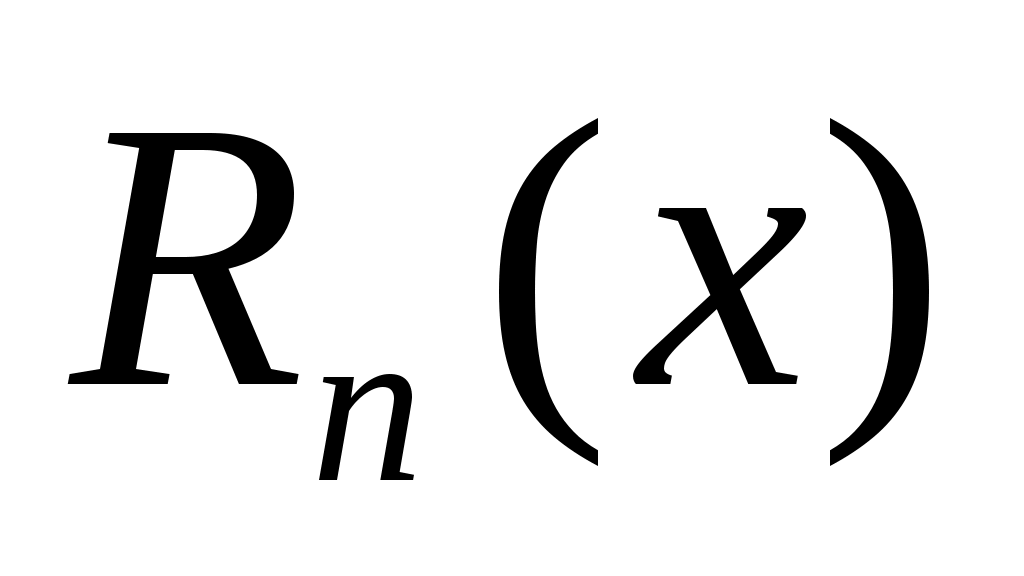 сходящегося ряда стремится к нулю.
сходящегося ряда стремится к нулю.
3.2 Степенные ряды.
Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида.
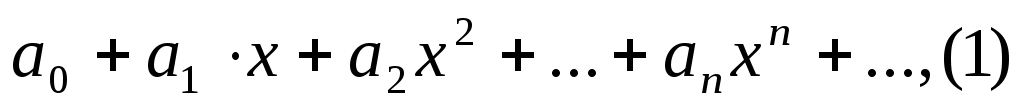
Или более общего вида
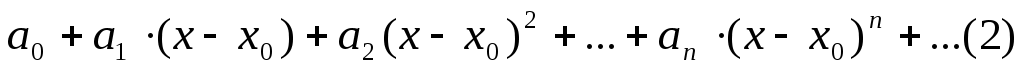
Где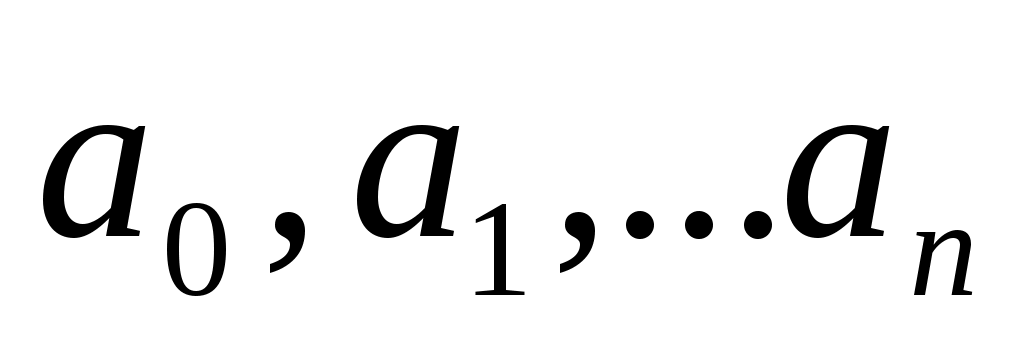 - постоянные числа, называемые коэффициентами ряда.
- постоянные числа, называемые коэффициентами ряда.
Ряд (2) подстановкой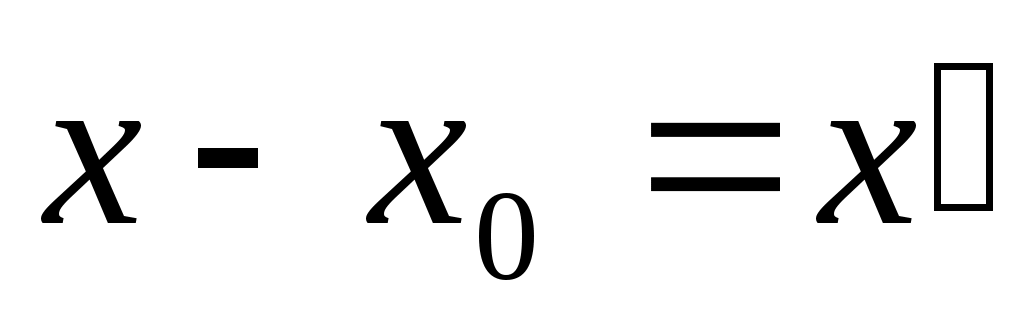 преобразуется в ряд вида (1), поэтому в дальнейшем будем заниматься рядами вида (1).
преобразуется в ряд вида (1), поэтому в дальнейшем будем заниматься рядами вида (1).
Теорема Абеля.
Если степенной ряд (1) сходится при некотором значении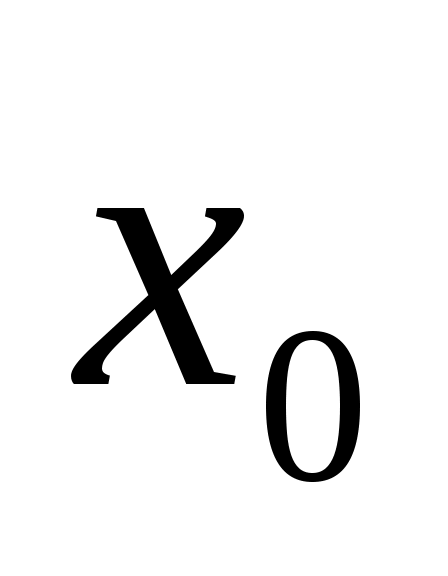 , не равном нулю, то он абсолютно сходится при всяком значении
, не равном нулю, то он абсолютно сходится при всяком значении  , для которого
, для которого 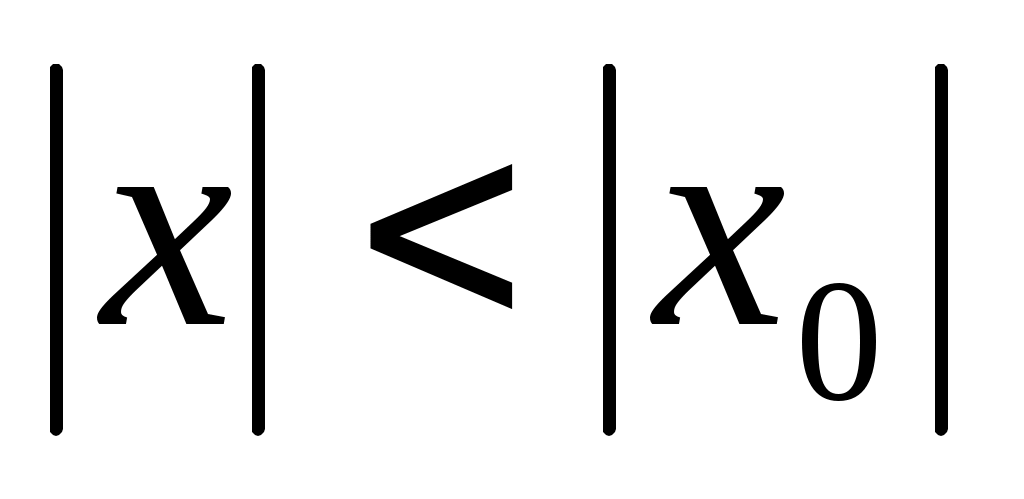 ;
;
Если ряд расходится при некотором значении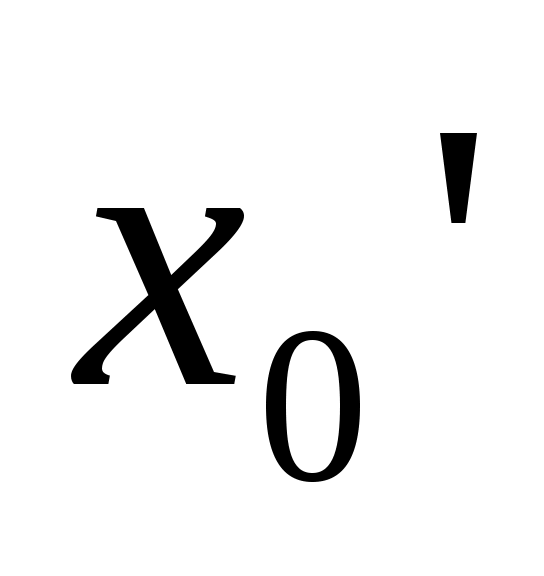 , то он расходится при всяком
, то он расходится при всяком  , для которого
, для которого 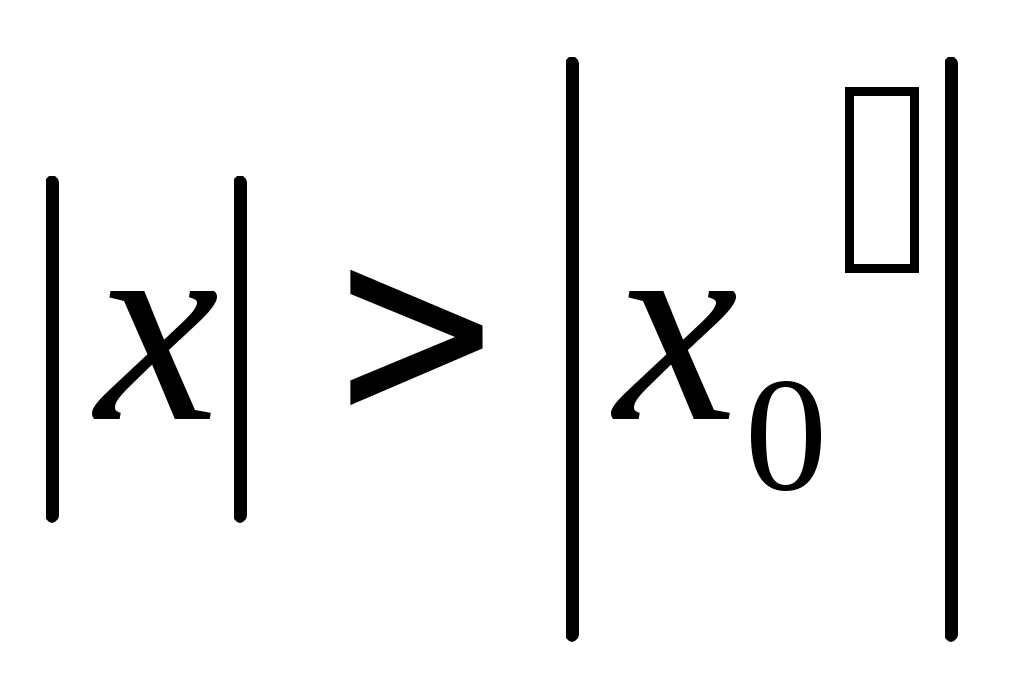
Из теоремы Абеля следует, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число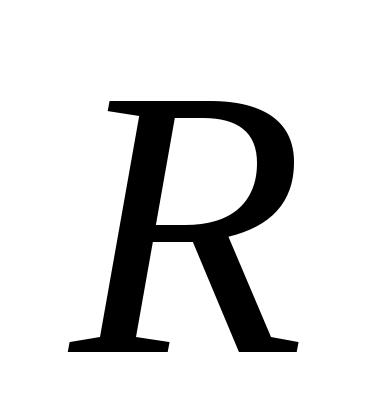 , что для всех
, что для всех 
, по модулю меньших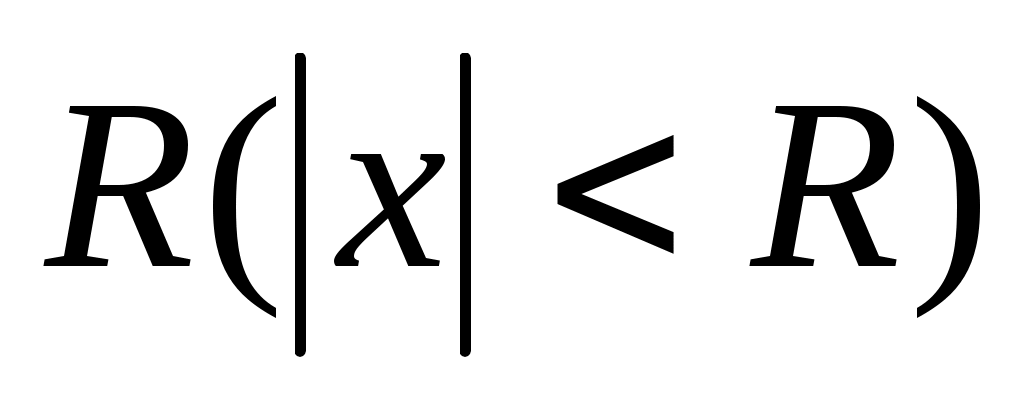 ряд абсолютно сходится, а для всех
ряд абсолютно сходится, а для всех  , по модулю больших
, по модулю больших 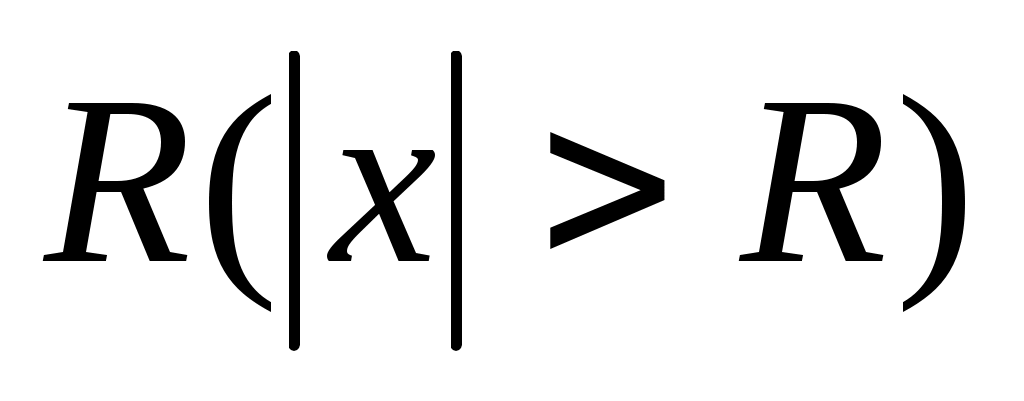 , ряд расходится.
, ряд расходится.
Определение. Радиусом сходимости степенного ряда (1) называется такое число , что для всех
, что для всех  ,
, 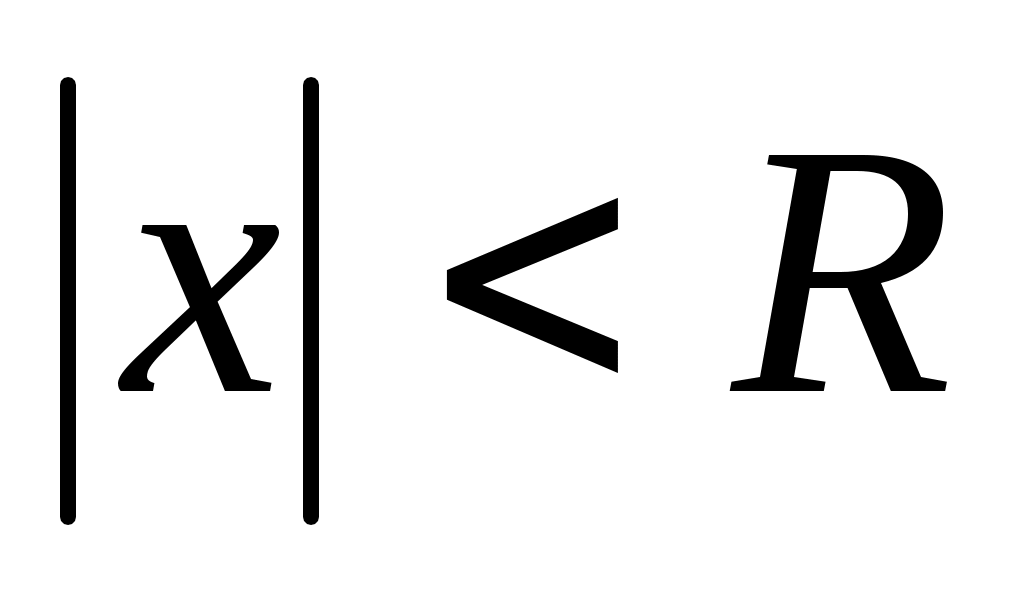 , степенной ряд сходится, а для всех
, степенной ряд сходится, а для всех 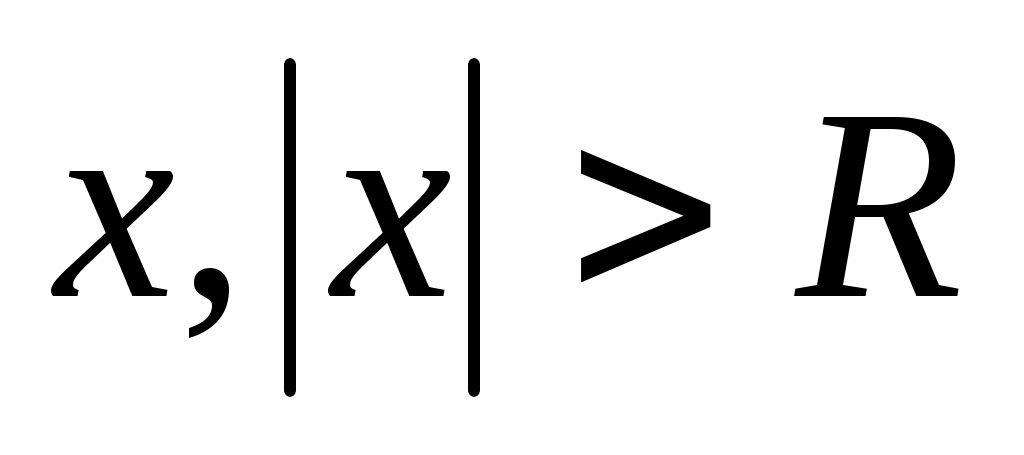 , расходится. Интервал
, расходится. Интервал 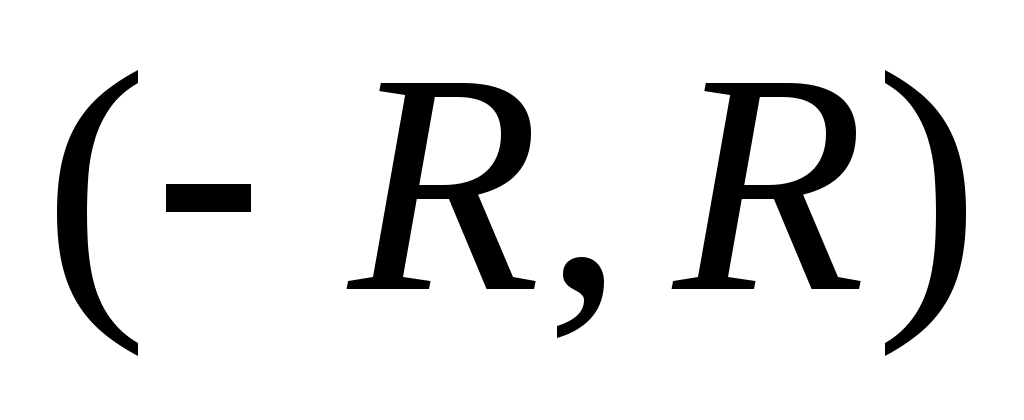 называется интервалом сходимости.
называется интервалом сходимости.
3.3. Определение интервалов сходимости степенных и функциональных рядов.
Пусть имеем ряд
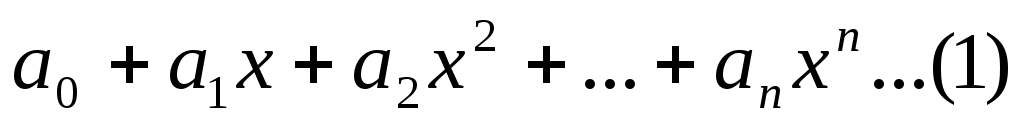
Рассмотрим ряд, составленный из абсолютных величин его членов.
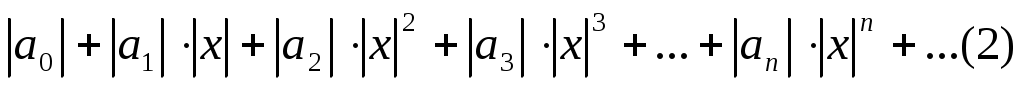
Для определения сходимости этого ряда с положительными членами применим признак Даламбера. Допустим, что существует предел:
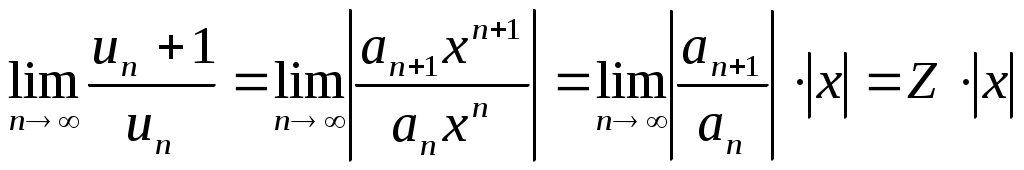
По признаку Даламбера ряд (2) сходится, если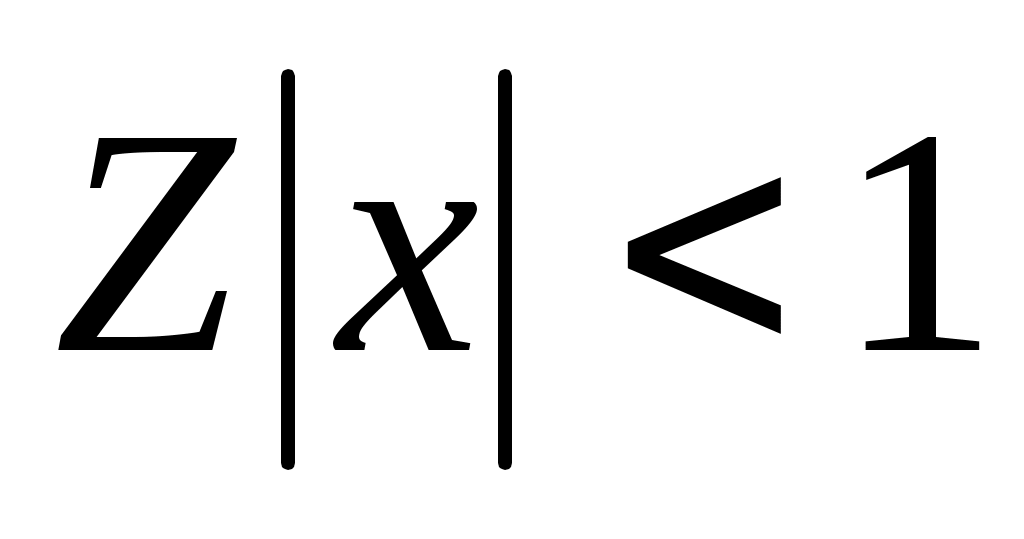 , т.е. если
, т.е. если 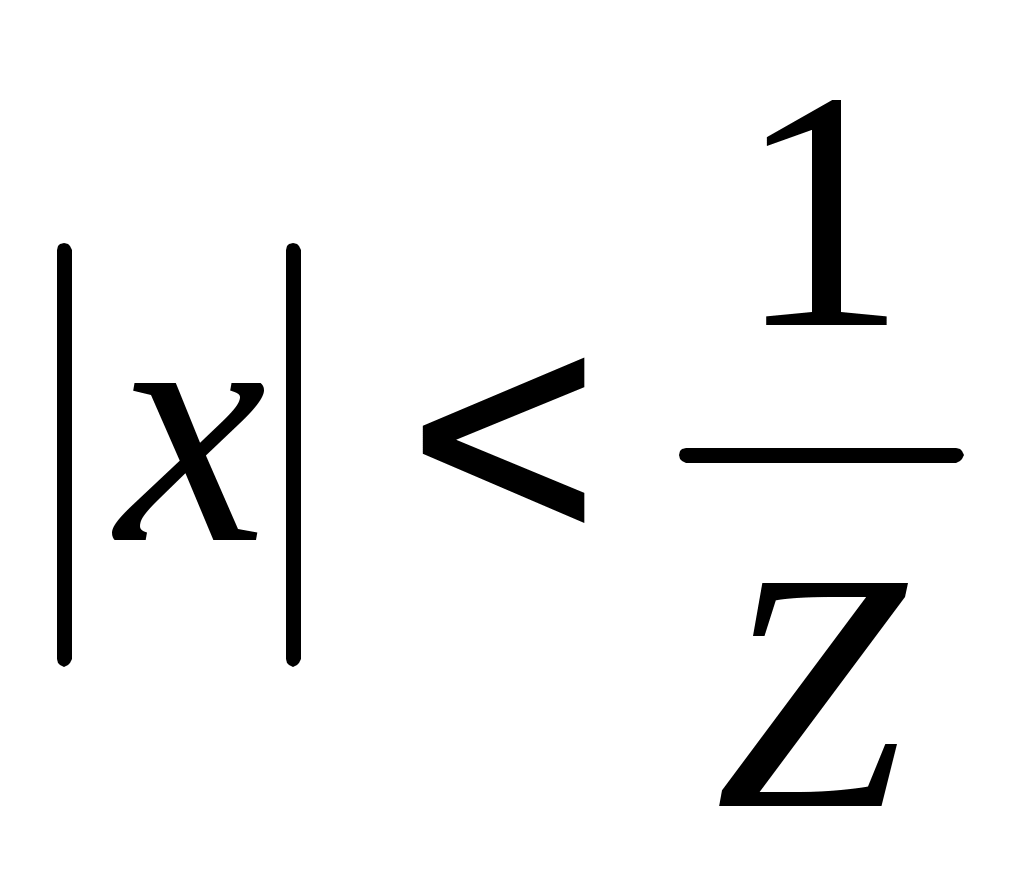 , и расходится, если
, и расходится, если 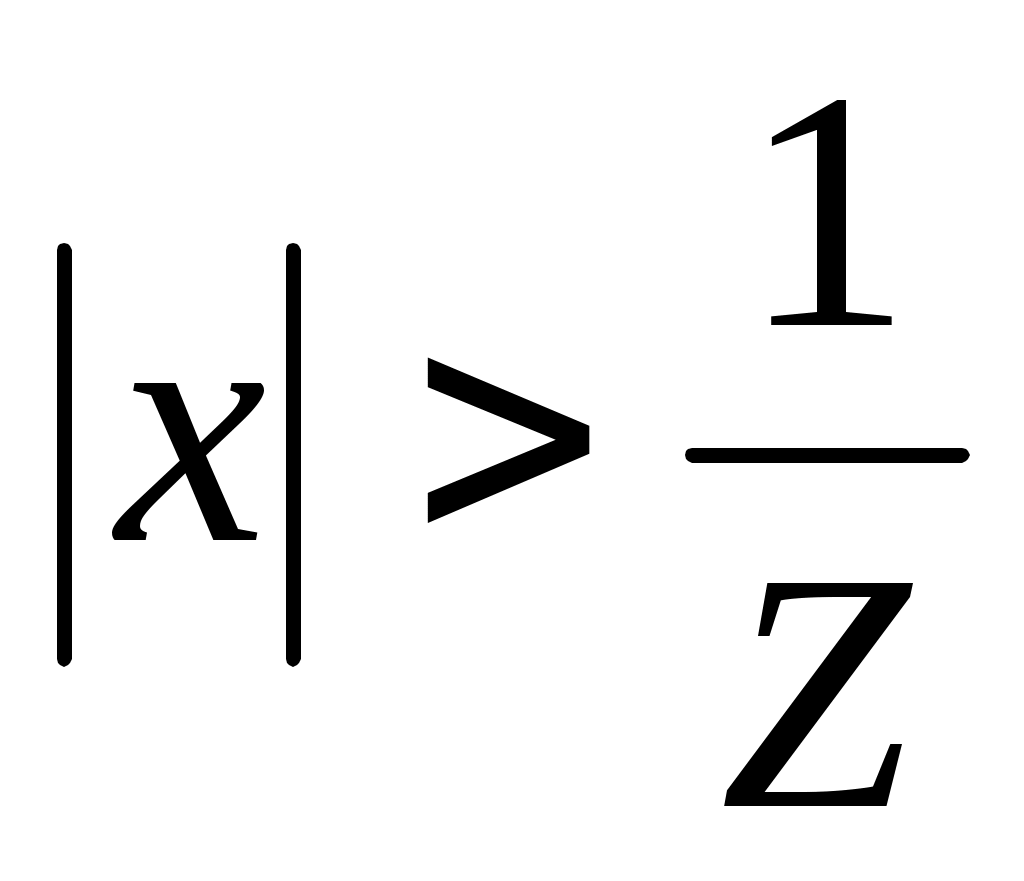 . Следовательно, ряд (1) сходится абсолютно, при
. Следовательно, ряд (1) сходится абсолютно, при 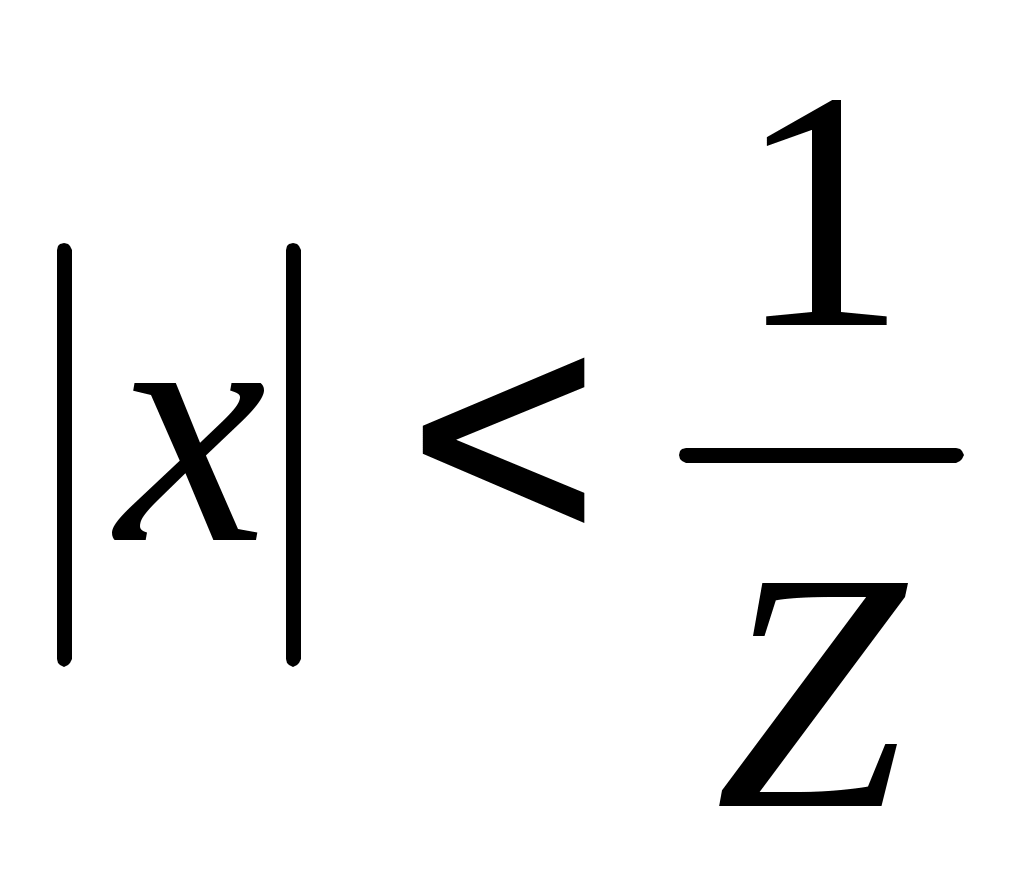 , а если
, а если 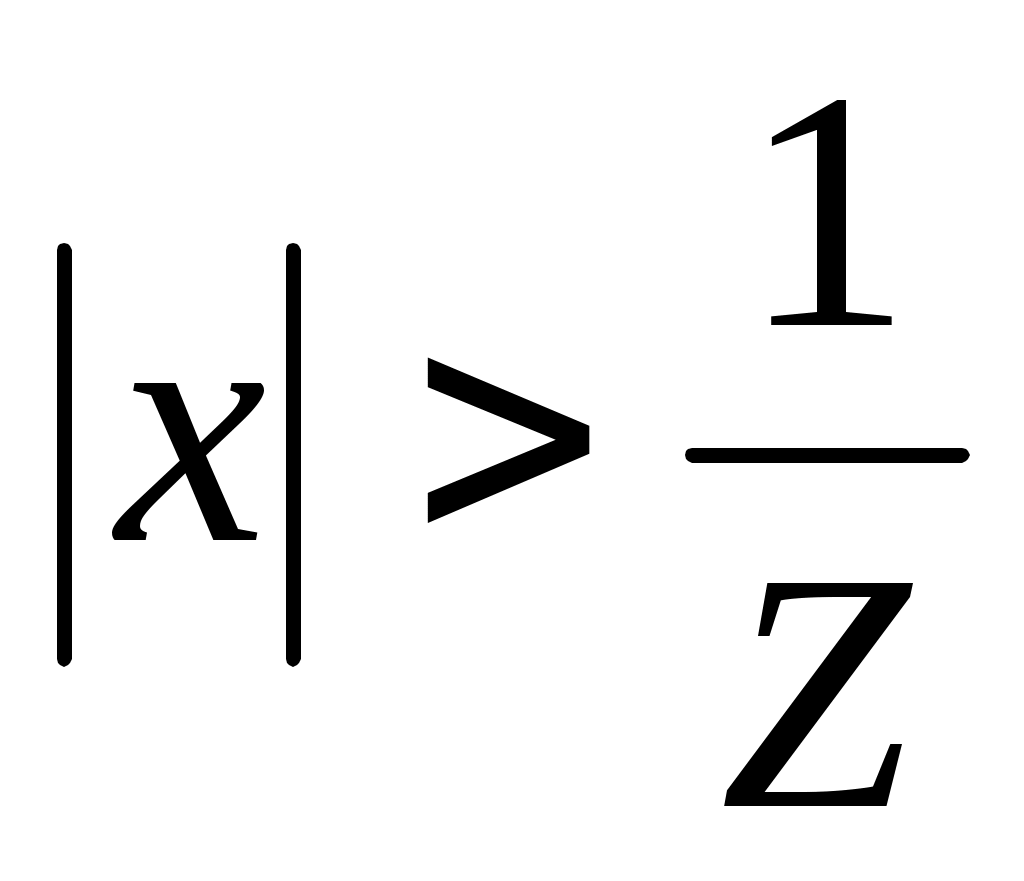 , то
, то
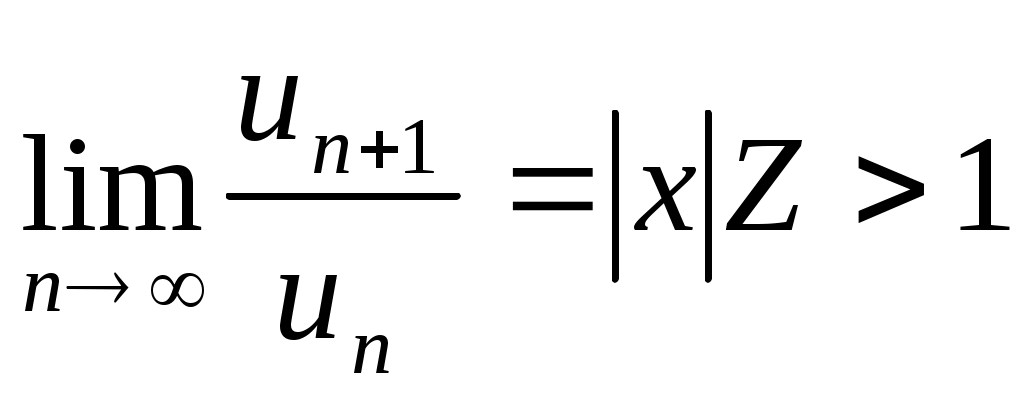 и ряд (2) расходится, причем его общий член не стремится к нулю ( не выполняется необходимый признак сходимости), а значит, ряд (1) расходится.
и ряд (2) расходится, причем его общий член не стремится к нулю ( не выполняется необходимый признак сходимости), а значит, ряд (1) расходится.
Интервалом сходимости ряда (1) является интервал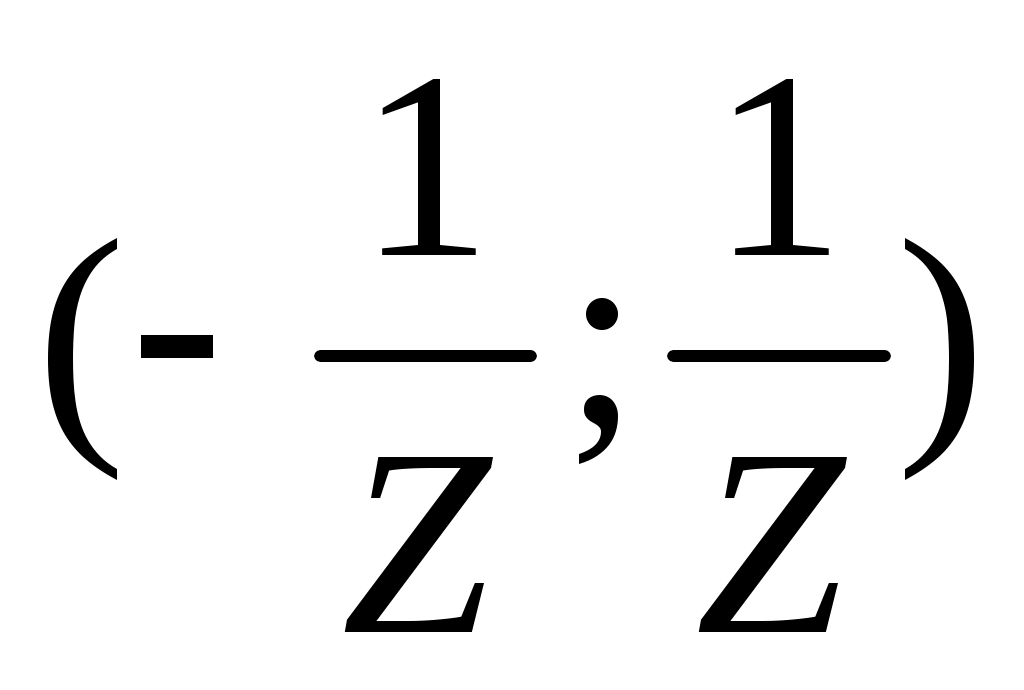 , а радиус сходимости
, а радиус сходимости 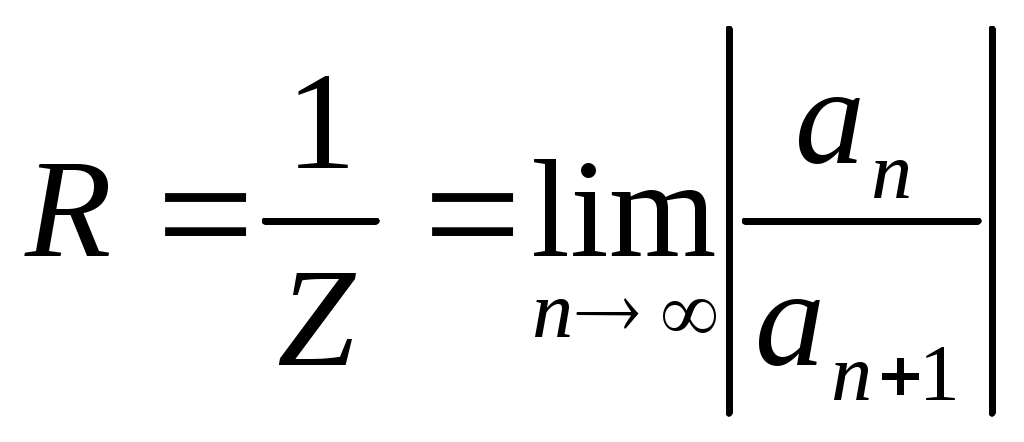
При исследовании вопроса о сходимости ряда на концах интервала сходимости признак Даламбера не применим т.к. соответствующий предел здесь равен единице, поэтому здесь надо применить какой-либо другой признак.
Пример. Определить интервал сходимости степенного ряда:
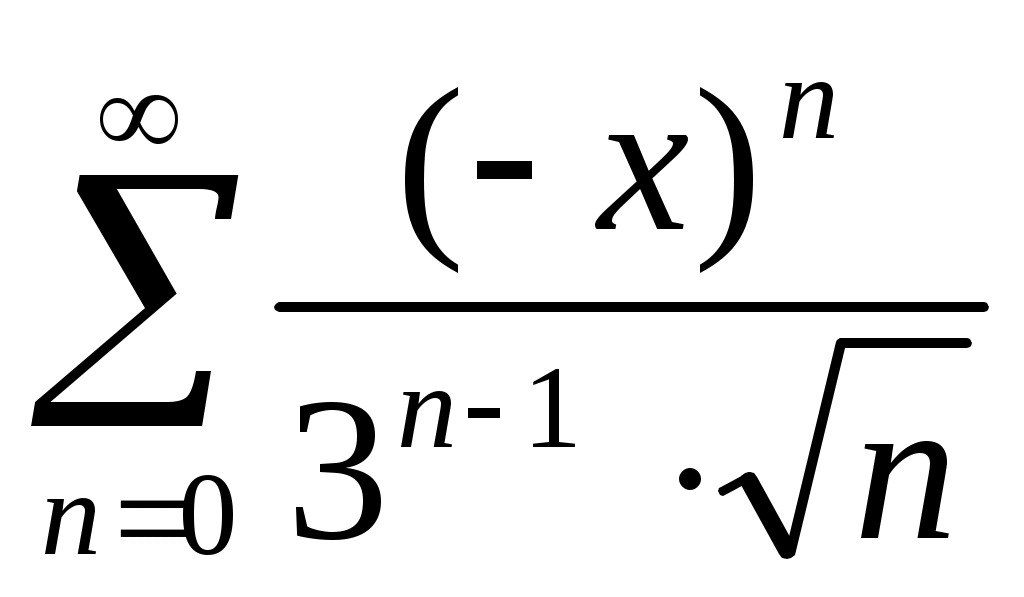
Составляем ряд из модулей: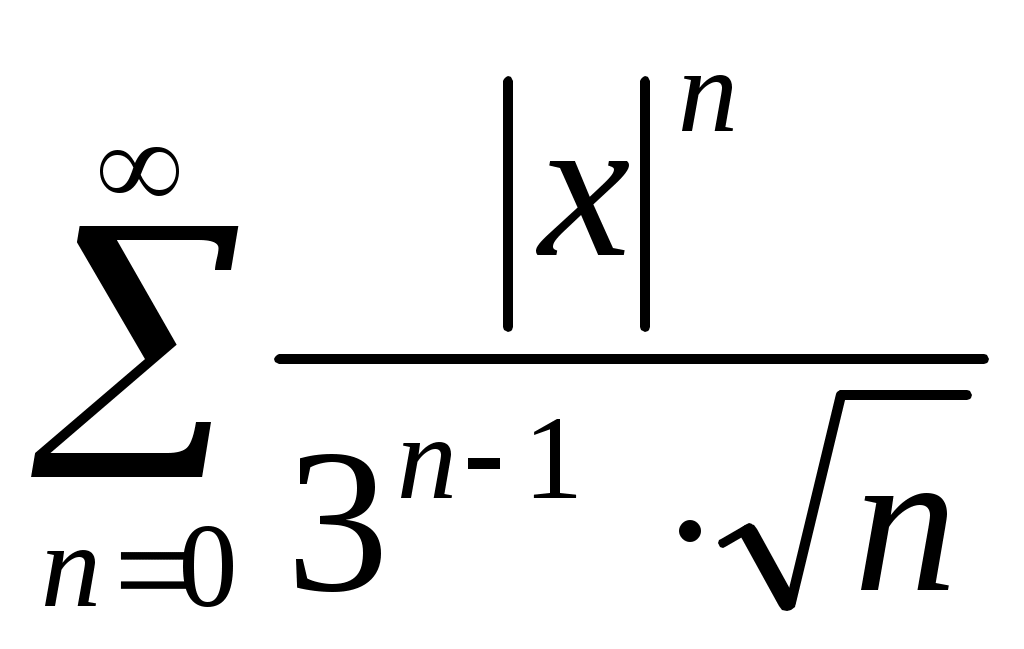
Как следует из ряда,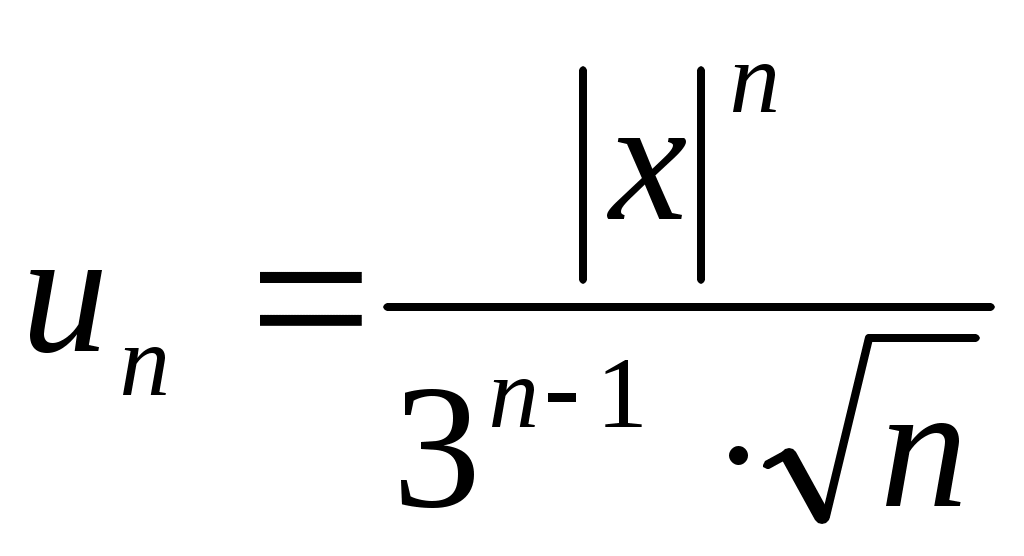 ,
, 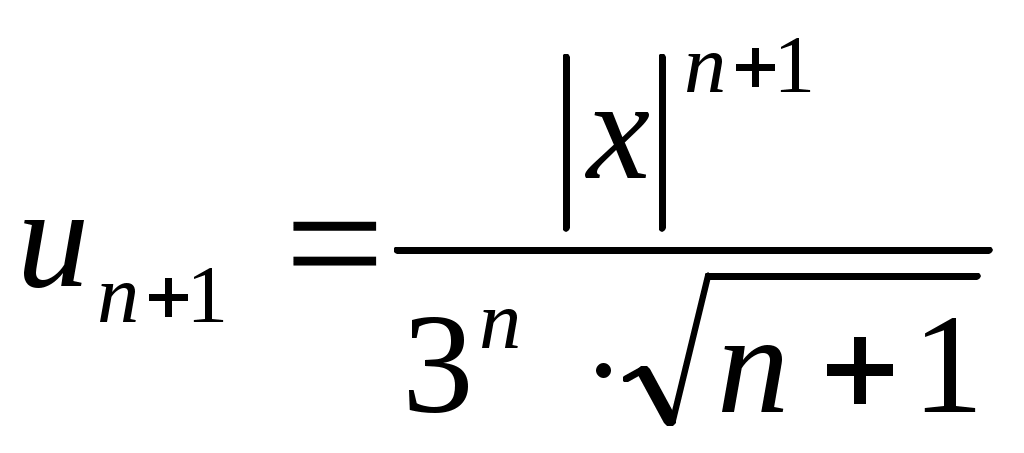
Далее, используя признак Даламбера, ищем предел
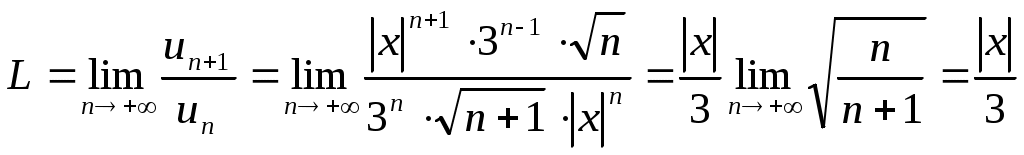
И определяем, при каких значениях этот предел будет меньше единицы, т.е. решаем неравенство
этот предел будет меньше единицы, т.е. решаем неравенство 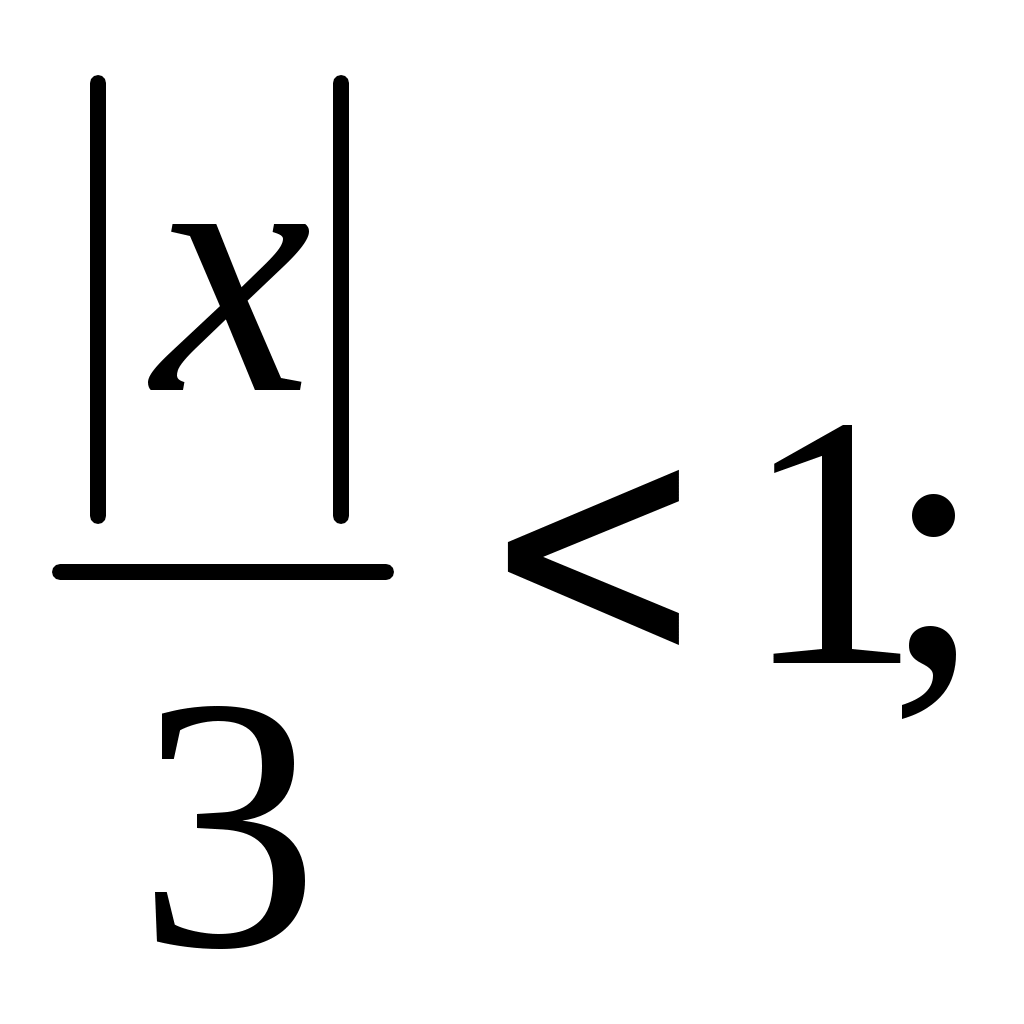
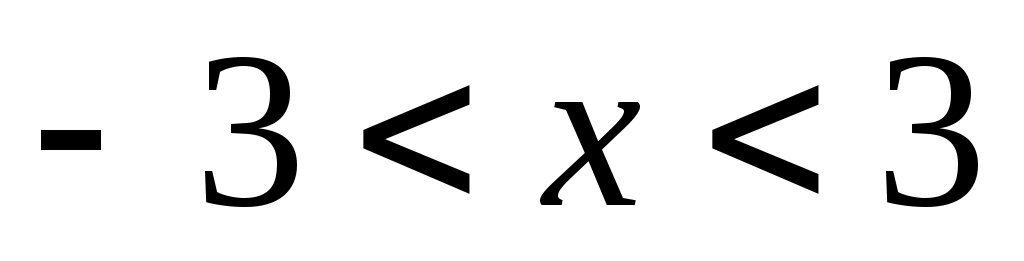
Согласно признаку Даламбера, при любом значении из найденного интервала данный ряд сходится (абсолютно), а при
из найденного интервала данный ряд сходится (абсолютно), а при 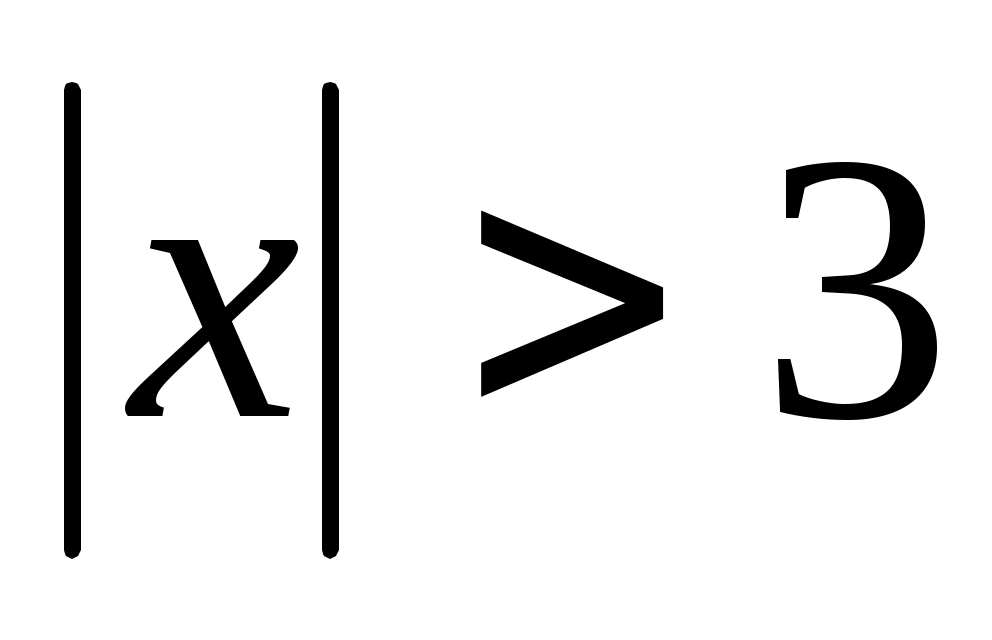 расходится.
расходится.
Граничные точки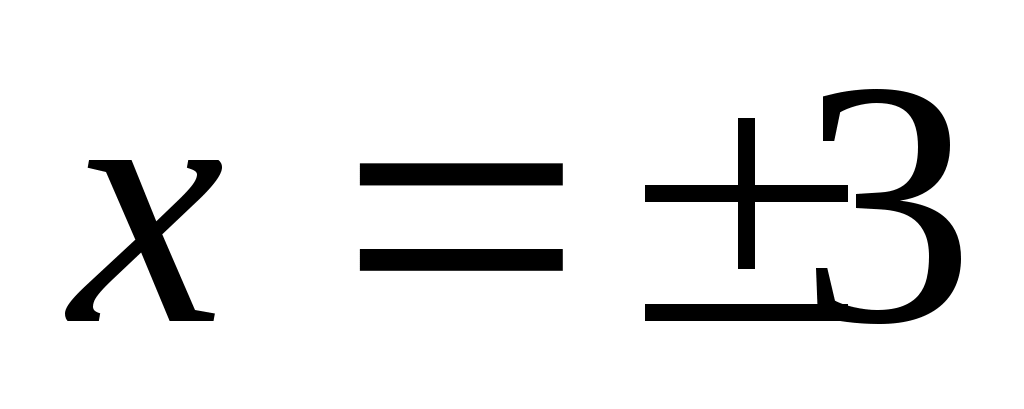 этого интервала, для которых
этого интервала, для которых 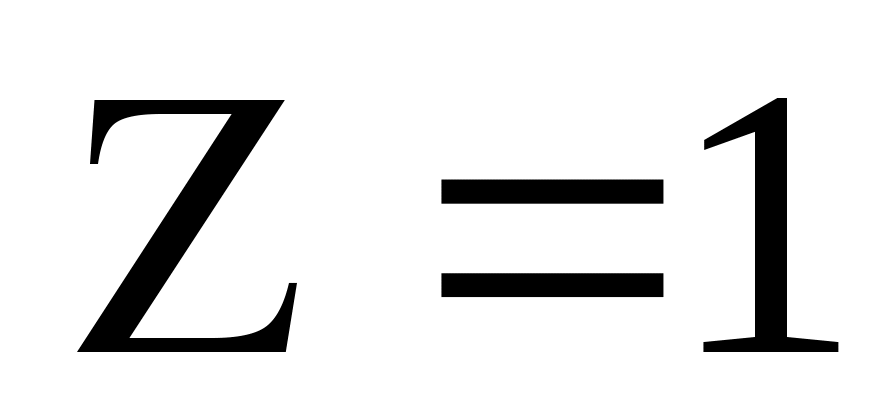 и признак Даламбера не решает вопроса о сходимости ряда, исследуем особо.
и признак Даламбера не решает вопроса о сходимости ряда, исследуем особо.
При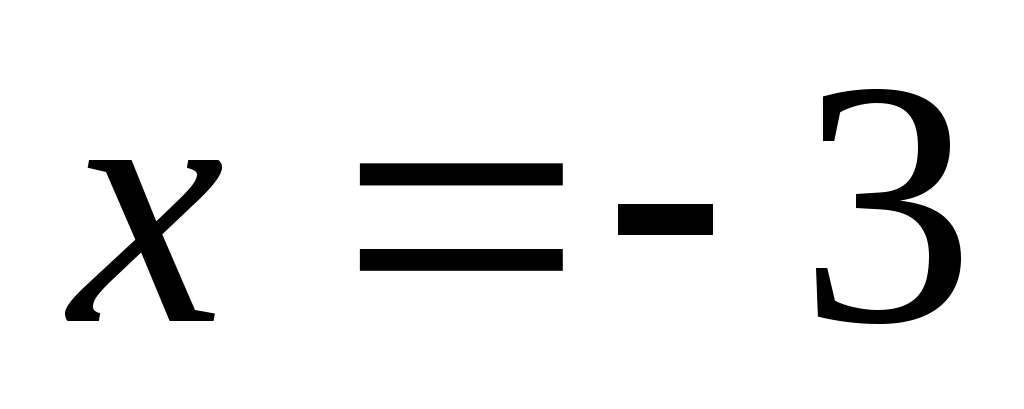 получим числовой ряд с положительными членами
получим числовой ряд с положительными членами 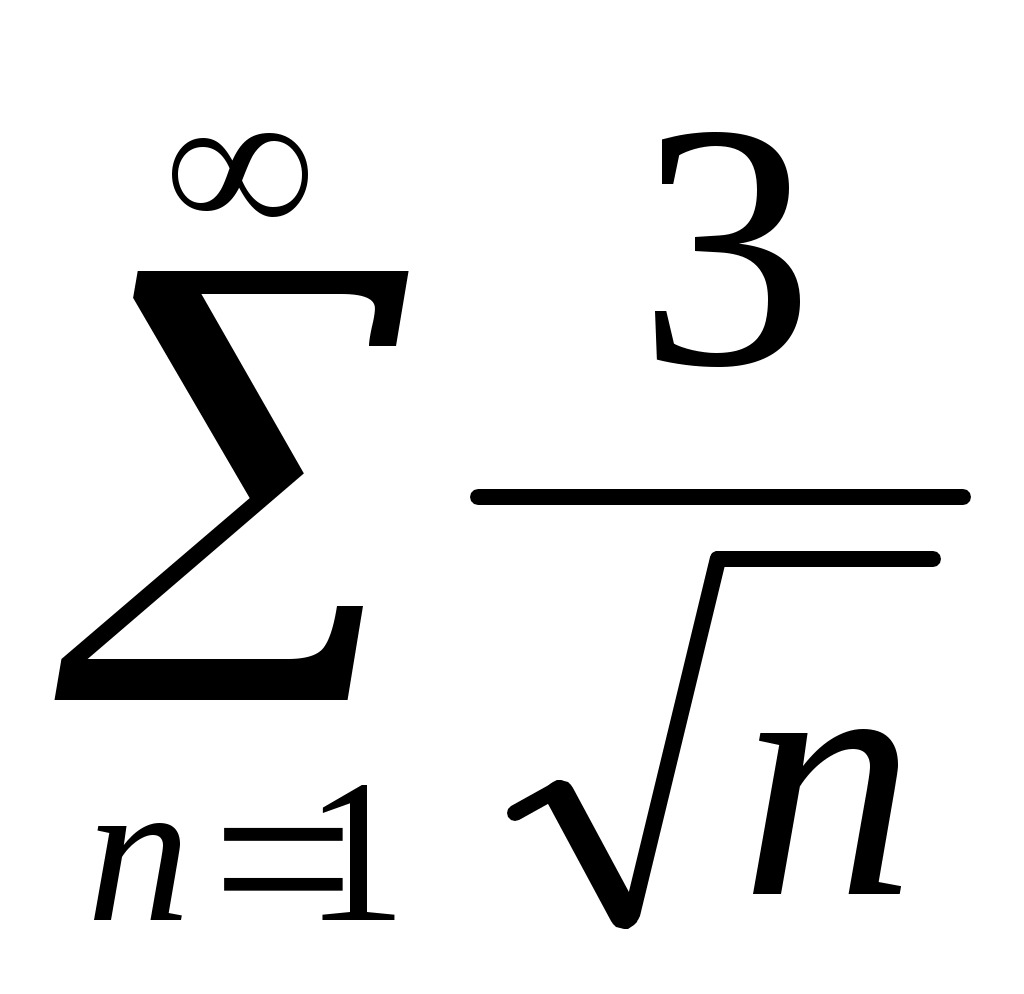 , который расходится, что следует из сравнения его с расходящимся гармоническим рядом
, который расходится, что следует из сравнения его с расходящимся гармоническим рядом 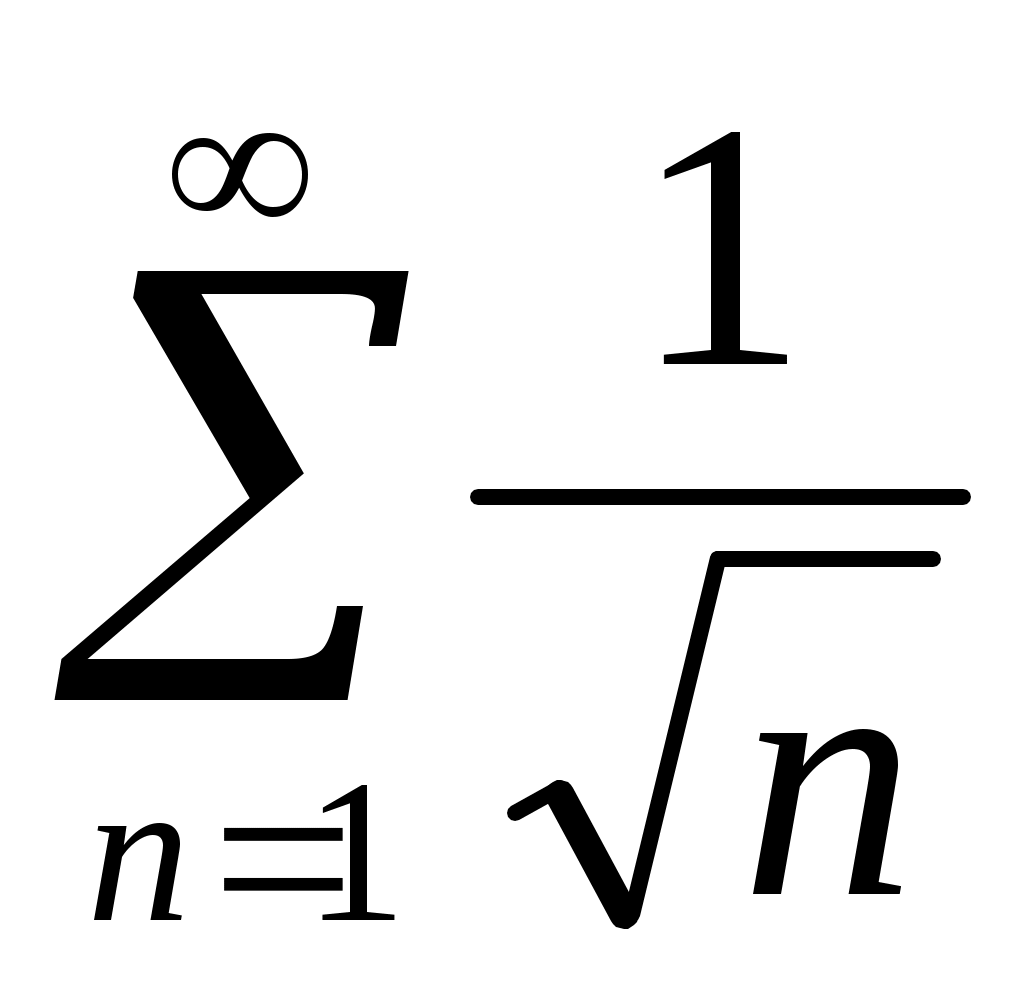
При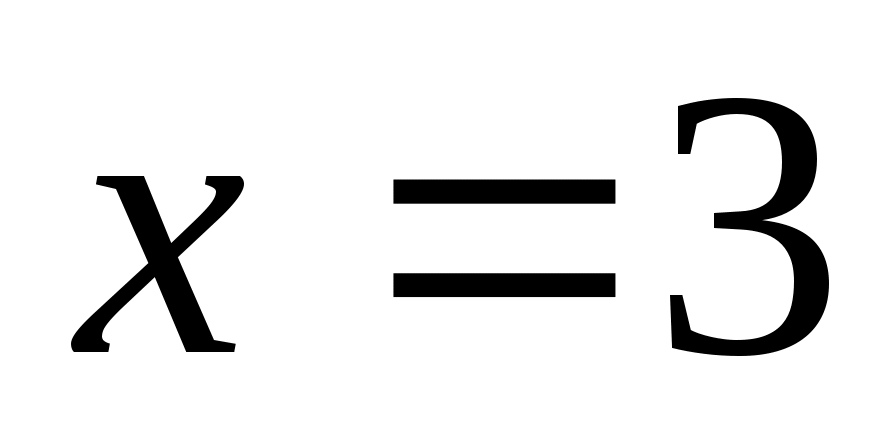 получим числовой знакочередующийся ряд
получим числовой знакочередующийся ряд 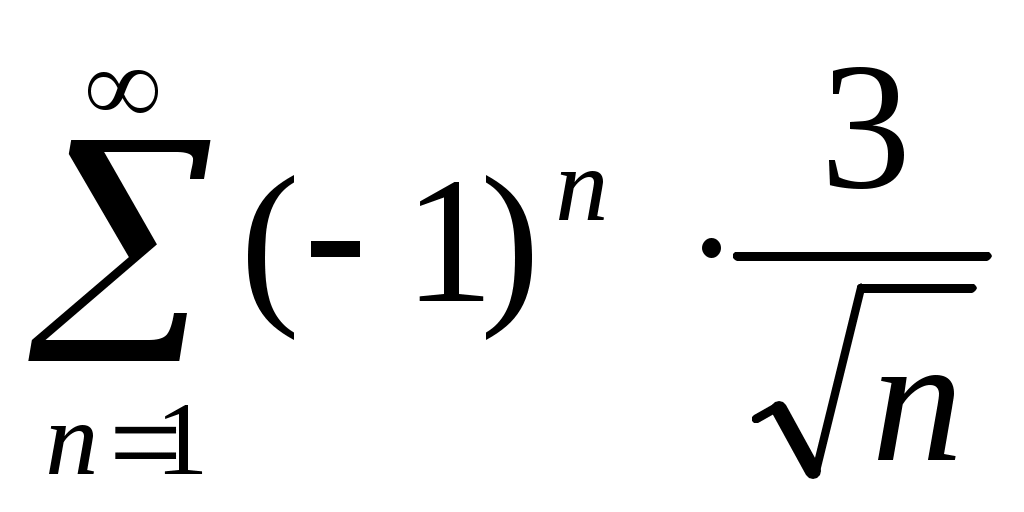 , который сходится согласно признаку Лейбница. Члены ряда убывают по абсолютному значению, стремясь к нулю. Следовательно, интервалом сходимости данного степенного ряда является полуоткрытый интервал
, который сходится согласно признаку Лейбница. Члены ряда убывают по абсолютному значению, стремясь к нулю. Следовательно, интервалом сходимости данного степенного ряда является полуоткрытый интервал 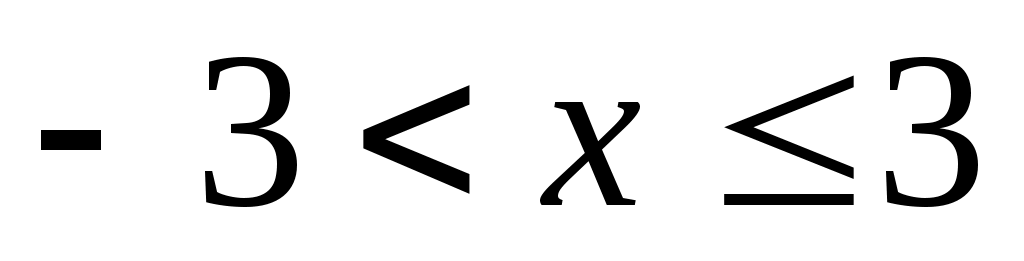
3.4 Свойства степенного ряда.
1. Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда.
2. Если степенной ряд
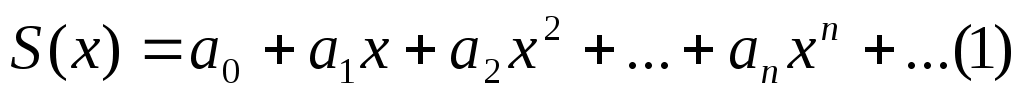
имеет интервал сходимости (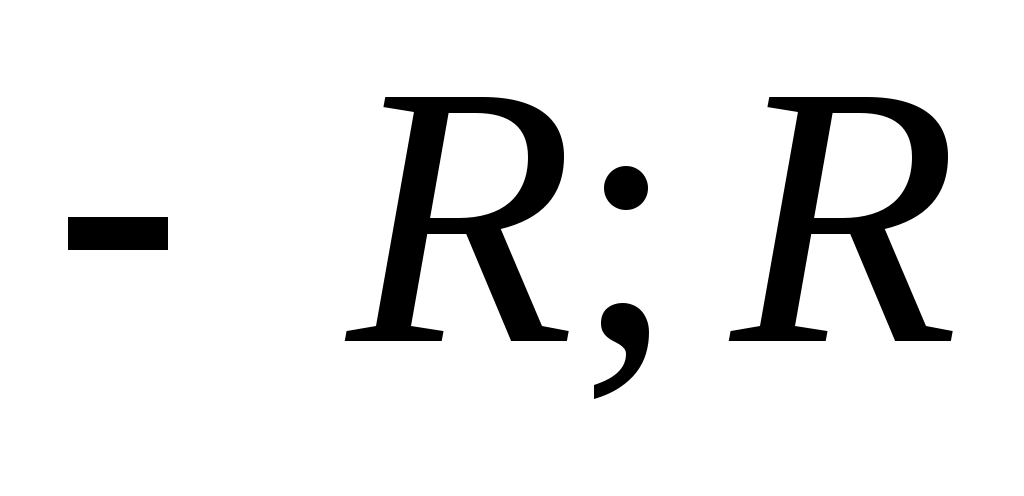 ), то ряд
), то ряд
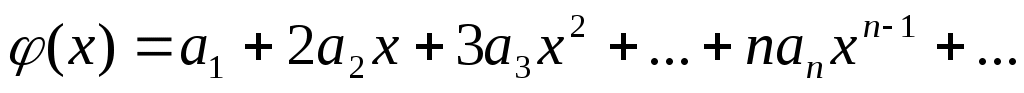 ,
,
полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимости (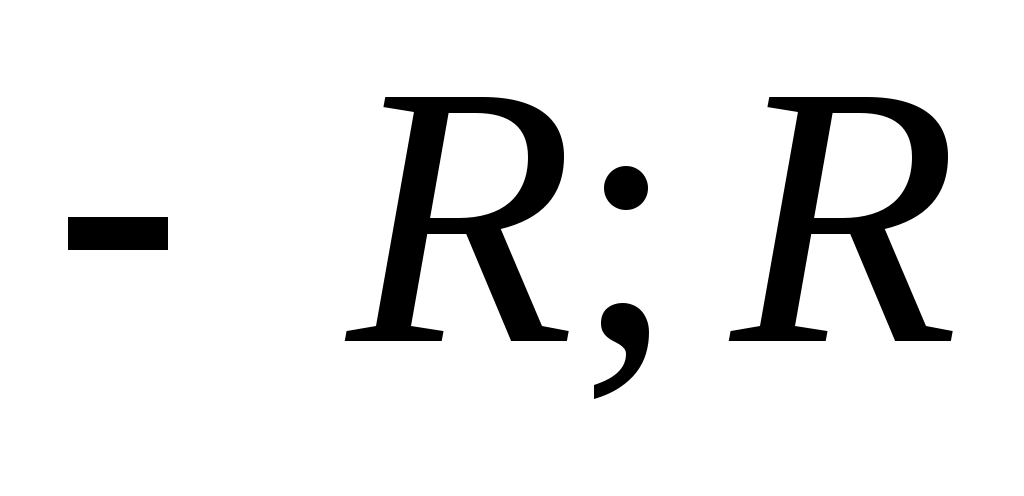 ), при этом
), при этом 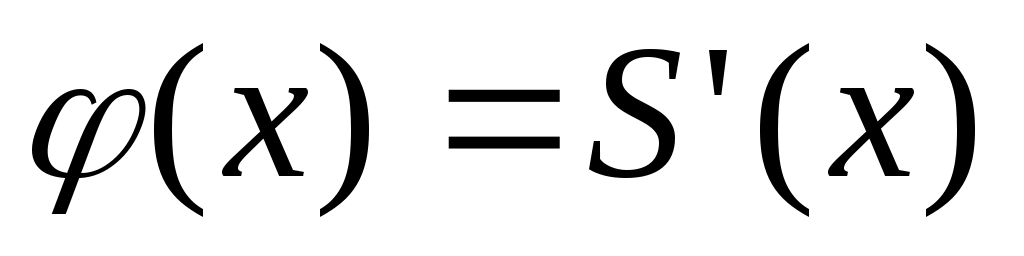 ,если
,если  , т.е внутри интервала сходимости производная от суммы степенного ряда (1) равна сумме ряда, полученного почленным дифференцированием ряда (1).
, т.е внутри интервала сходимости производная от суммы степенного ряда (1) равна сумме ряда, полученного почленным дифференцированием ряда (1).
3. Степенной ряд можно почленно интегрировать в интервале сходимости
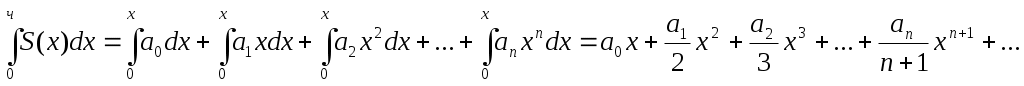
Задачи для решения.
В задачах 129-150 найти область сходимости степенных рядов:
129)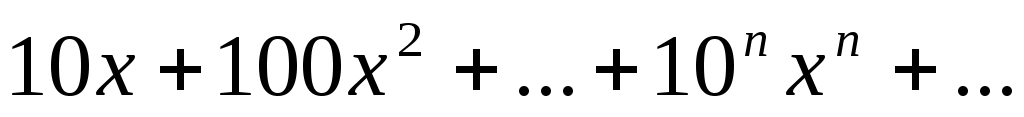
130)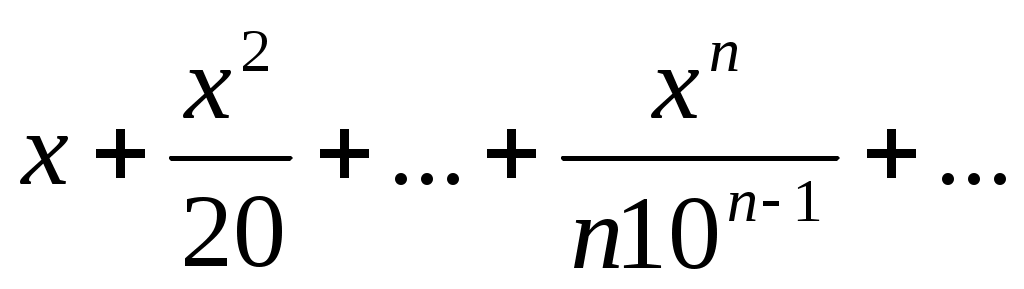
131)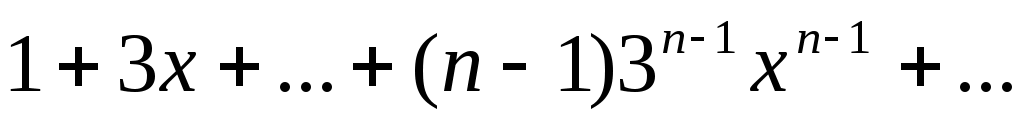
132)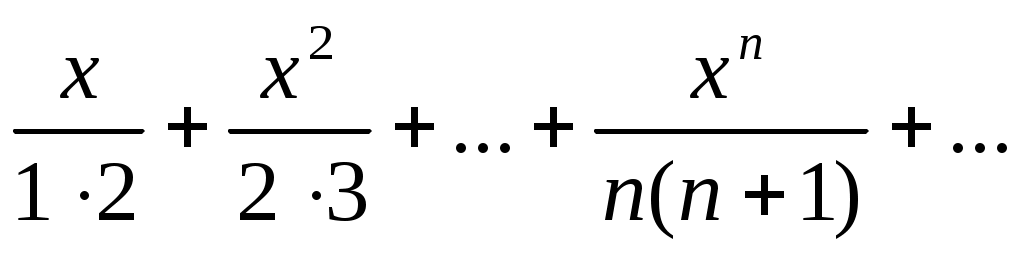
133)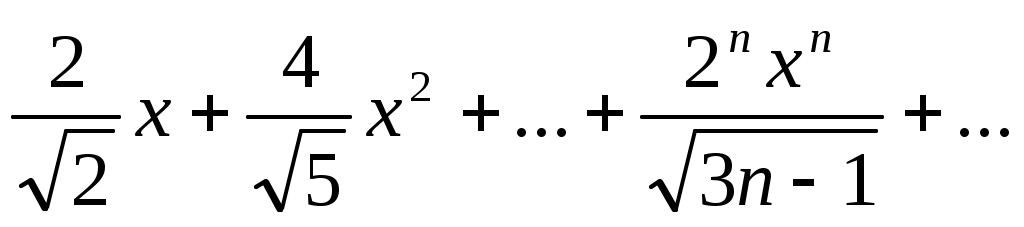
134)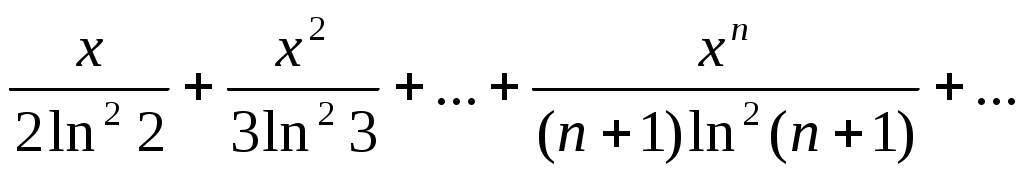
135)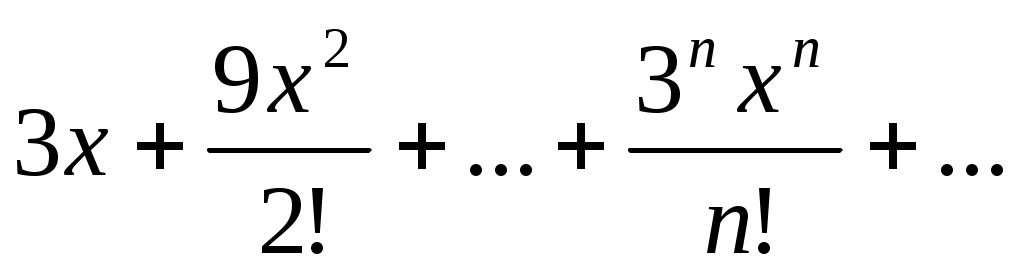
3.1 Основные определения.
Определение. Ряд
При различных значениях
Определение. Совокупность значений
В области сходимости ряда его сумма является некоторой функцией от
Пример. Функциональный ряд
В интервале сходимости сумма ряда
При всех
Обозначим
где
Поэтому
Т.е. остаток
3.2 Степенные ряды.
Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида.
Или более общего вида
Где
Ряд (2) подстановкой
Теорема Абеля.
Если степенной ряд (1) сходится при некотором значении
Если ряд расходится при некотором значении
Из теоремы Абеля следует, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число
, по модулю меньших
Определение. Радиусом сходимости степенного ряда (1) называется такое число
3.3. Определение интервалов сходимости степенных и функциональных рядов.
Пусть имеем ряд
Рассмотрим ряд, составленный из абсолютных величин его членов.
Для определения сходимости этого ряда с положительными членами применим признак Даламбера. Допустим, что существует предел:
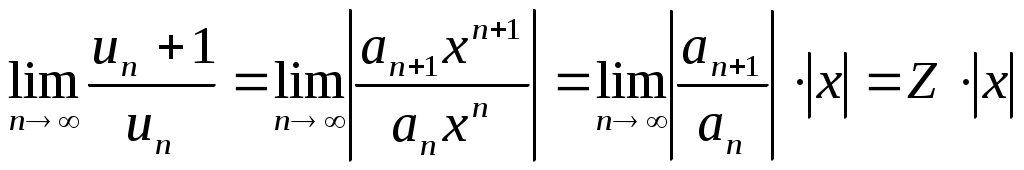
По признаку Даламбера ряд (2) сходится, если
Интервалом сходимости ряда (1) является интервал
При исследовании вопроса о сходимости ряда на концах интервала сходимости признак Даламбера не применим т.к. соответствующий предел здесь равен единице, поэтому здесь надо применить какой-либо другой признак.
Пример. Определить интервал сходимости степенного ряда:
Составляем ряд из модулей:
Как следует из ряда,
Далее, используя признак Даламбера, ищем предел
И определяем, при каких значениях
Согласно признаку Даламбера, при любом значении
Граничные точки
При
При
3.4 Свойства степенного ряда.
1. Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда.
2. Если степенной ряд
имеет интервал сходимости (
полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимости (
3. Степенной ряд можно почленно интегрировать в интервале сходимости
Задачи для решения.
В задачах 129-150 найти область сходимости степенных рядов:
129)
130)
131)
132)
133)
134)
135)