Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx
Добавлен: 07.12.2023
Просмотров: 116
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1
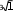 3
3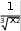 x1
x1 0,1 1,033.
-
Вычислить приближенно sin 46 .
Решение
y sin x,
x 45 ,
x 1.
sin 45 1 sin sin cos
2 2
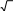
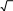 4 180
4 180 4
2 2 180
0,7194 .
4 180
4. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
-
Свойства производных (правила дифференцирования). -
Производная обратной функции. -
Производные элементарных функций.
-
Свойства производных (правила дифференцирования)
1. fx c, fx 0 .
2. fx gx
fx gx .
3. fx gx
fx gx
fx gx.
4. c f x c fx.
fx
5. gx
fxgxfxgx
g2 x
( gx 0).
Пример
y 3sin x 5log 2 x10 .
y 3cos x 5 log e.
x2
1 2 3 4 5 6 7 8 9
Свойства дифференциалов
Свойства дифференциалов аналогичны свойствам производных (предполагаем, что все рассматриваемые функции дифференцируемы).
1.
y c,
y 0,
2.
y u v,
y u v,
3.
y1 u c,
y2 u,
4.
y cu,
y cu,
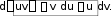 – константу можно выносить за знак дифференциала. 5.
– константу можно выносить за знак дифференциала. 5. Если
Если6.
-
d u
v
vdu udv
v2
Производная обратной функции
Теорема
, vx 0 .
-
fx строго монотонна и непрерывна в окрестности точки
2) fx0 0,
то
x0 ;
 1) f1y в окрестности точки 2)
1) f1y в окрестности точки 2)y0
fx0 ;
Доказательство
Из условия 1 следует существование непрерывной обратной функции
x f1y
в окрестности точки
y0
fx0
(см. «Элементарные
функции» в «Математический анализ. Введение»).
Приращению аргумента y
соответствует приращение функции
x.
Рассмотрим их отношение
x
y
1 . (*)
y
x
Из строгой монотонности функции
fx
следует, что условие
y 0
влечет за собой x 0 .
Устремим y
к нулю. Из непрерывности функции
x f1y следует,
что x 0 .
Но при
x 0 ,
y
x
fx0
, следовательно,
x
y
1
fx0
(см. (*)).
То есть
f1 y y y
1 , что и требовалось доказать.
0
Применение
0 fx
-
y ax x log y.
a
ax 1 1 y axln a.
log a
y
1 log e y a
log ae
ex ex.
-
y arcsin x x sin y.
arcsin x
1
sin y
1 1 cos y
1 .
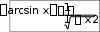

 3.
3.4. arctg x
1
tg y
cos2 y
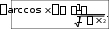 1
11 tg 2 y
1 .
1 x2
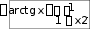
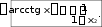 5.
5.- 1 2 3 4 5 6 7 8 9