Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 119

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

«
1
2
3
4
5
6
7
8
»

Производная неявной функции

Уравнение

y fx^{, разрешенное относительно}^y^{, задает}^явную

функцию yаргумента x.

Уравнение

Fx, y  0^,^{неразрешенное}^{относительно}^y^,^задает^{неявную}

функцию yаргумента x.

Пример

_x2  _y2

_a2 _b2
^^1,y^^–^?

Решение

Способ 1.
Переход к явной функции

y  ^b

a

^a²^^x²

y^  ^b

a

 ¹a²

2

x²

 ²  2x  ^b

_1

∓
a

x



.

a²  x²

Способ 2. В условии
_x2  _y2

_a2 _b2

 1 записано равенство двух выражений, или двух

функций одного независимого аргумента x. Если равны функции, то

равны и их производные

2x 2 y __^b²^x

Правило

 y

_a2 _b2

^⁰

^y^^_a₂^_y.

Чтобы найти первую производную от функции, заданной неявно, нужно одинраз продифференцировать равенство, задающее эту функцию, считая yфункцией аргумента x.

Примеры

1. Записать уравнение касательной к эллипсу

M₀x₀, y₀^.

Решение

y y₀ y^x₀x x₀^,

_x2  _y2 



1
_a2 _b2
в точке

^    ^b2

_x₀

yx₀

,

a² ^y⁰

y y₀

  ^b2 ^x⁰ 

x
a² y₀

x₀.

x₀x		y₀y		1.
_a2	_b2

2. y²  2 px.

y^^–^?

Решение

2y y^ 2 p^,
^y^^^p.

y

1 2 3 4 5 6 7 8 9

Логарифмическая производная

Пусть

fx  0^,

f^x^.

Для вычисления

f^x

в ряде случаев полезен прием предварительного

логарифмирования выражения, задающего функцию.

Рассмотрим равенство

y fx^.

Выполним его почленное логарифмирование

ln y ln

fx^.

Дифференцирование последнего равенства

ln y^ ln  fx^

приводит к отношению

производной.

Применение

^y^ ln  fx^, которое называется логарифмической

y

1. ^y^^x^,  – любое действительное число.

ln y  ln x

  ^^

y' _ _

^   ^x  

1

ln y   y x .

x y x x

x^ ^ x^¹ _.

y sin x^x2
2. 

ln y x² ln sin x.

y^_

y
2xln

sin x 

_x2 

sin x
^cos^x.

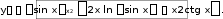
В общем случае для степенно-показательных выражений.

y ux^v^^x^
 ln

y vx ln ux^.

^y^ v^xln ux  ^v^^x^ u^x.

y ux

Для произведения более двух функций.

^y^^sin^x^^cos^x^^x^,y^^–^?

^ln^y^^ln^sin^x^^ln^cos^x^^ln^x;

y^_cos x_ sin x_1

 y^ xsin xcos x^ctg x tg x ¹^.

y sin x cos x x

__x_

1 2 3 4 5 6 7 8 9

Производные гиперболических функций

 
_ex__e x

sh x ,

2

ch x

_ex__e x

 ,

2

th x 

_ex__e x

_ex__e x
, cth

x 

_ex__e x

_ex__e x^.

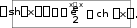
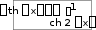
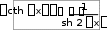( x 0 ).

Пример

y sh³5x cos² ^x.

2

y^ 3sh ² 5x ch5x 5  cos² ^x sh³5x 2 cos ^x ^ sin

x__1 _

2

 sh ² 5x cos ^x^15ch 5x cos ^x sin

 

2

2

2
 

^x sh 5x^.

 

2

2

2
 

Производная функции, заданной параметрически

Рассмотрим функцию, заданную параметрическим способом

_x xt ,


^y yt.

В этом случае связь аргумента x со значением функции y

«
1
2
3
4
5
6
7
8
»

Смотрите также файлы

Эссе по психологии.docx

Интерактивные методы обучения на уроках истории.docx

Рекомендованные фразы и выражения для написания дневника пп в поликлиники.docx

Контрольная работа по дисциплине Методы принятия управленческих решений Темы.docx

Вопросы экзаменационных билетов.doc