ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 140
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Случайные события и предмет теории вероятностей.
1. Наблюдаемые нами события можно подразделить на три вида: достоверные, невозможные, случайные.
-
Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 200 (совокупность условий S), то событие «вода в сосуде находится в жидком состоянии» есть достоверное. -
Невозможным называется событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S. Например, событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера. -
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например, брошенная монета может упасть либо «орлом», либо «решкой». Поэтому событие «при бросании монеты выпал «орел»» - случайное. Каждое случайное событие есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета, форма монеты и многих других). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет. -
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, хотя, наперед нельзя определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений «орла», если монета брошена достаточно большое число раз. При этом предполагается, что монету бросают в одних и тех же условиях.
-
Операции над событиями: сумма событий, произведение событий, дополнение событий, противоположное событие.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Дополнением события до называется событие, состоящее в том, что произошло, но не произошло. Событие содержит элементарные исходы, входящие в множество, но не входящие в. Противоположным (или дополнительным) к событию называется событие, состоящее в том, что не произошло.
-
Совместные события, полная группа событий.
а) События называются СОВМЕСТНЫМИ, если появление одного не исключает появление другого. В противном случае, они называются НЕСОВМЕСТНЫМИ.
Б) Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Сумма вероятностей событий, образующих полную группу, равна 1.
-
Понятие вероятности. Способы подсчета вероятностей.
Вероятность — степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным.
Существуют два способа определения вероятности события.
1. Теоретический способ основан на непосредственном (без проведения специального эксперимента) определении вероятности события по формуле:
P(A)=m/n,
где m - число случаев, благоприятствующих наступлению события А; n - число всех равновозможных случаев из полной группы несовместных событий.
2. Статистический способ основан на предварительном проведении большого числа испытаний. При этом подсчитывают вероятность по формуле:
h (A) = k / L,
где k - число появления события А, называемое частостью А; L - общее число событий, наступивших в некоторой серии испытаний при определенном неизменном комплексе условий; h (A) - статистическая вероятность события.
-
Правило сложения вероятностей.
Правило сложения вероятностей: если A и В несовместимые события, то вероятность того, что наступит хотя бы одно из двух событий. А или В, равна сумме их вероятностей. P (A + B) = P (A) + P (B).
-
Условная вероятность. Независимые события и правило умножения вероятностей.
Условной вероятностью
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
В частности, отсюда получаем
.События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий. Событие В называется зависимым, если вероятность P (B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается P A (B).
Правило умножения вероятностей: если A и В независимые события, то вероятность одновременного наступления обоих событий. А и В, равна произведению их вероятностей. P (A·B) = P (A) · P (B). Обратите внимание: Мы говорим о сумме событий, когда может наступить хотя бы одно из двух событий или А, или В, или оба вместе. Но приведенную формулу применяем только для несовместимых событий, т.е. в случае, если они не могут произойти вместе.
-
Формула полной вероятности, формула Байеса.
Если событие А может произойти только при выполнении одного из событий
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле 
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий , вероятности появления которых
. Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности , откуда 
Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса).
-
Формулы комбинаторики и их применение к подсчету вероятностей.
Формула размещения:
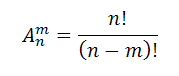
Формула перестановки: Рn=n!
Формула сочетания:
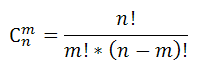
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
способами.Применение комбинаторики к подсчёту вероятностей
Многие задачи на предмет подсчёта вероятностей можно свести к так называемой схеме случайного выбора. Здесь, мы рассматриваем два основных варианта этой схемы: выбор с возвращением и выбор без возвращения.
1.Выбор с возвращением. Пусть
- некоторое множество элементов. Представим себе, в некотором ящике собрано n различных предметов, которые обозначены элементами. Из ящика наугад извлекается один из предметов, регистрируется, затем возвращается обратно в ящик. Если осуществить m раз таких действий, то получим некоторую строку длиною m, составленную из элементов множества 
. Полученная строка называется выборкой объёма из множества. Количество различных выборок объёмов соответствии с правилом произведения равно nm.Вероятность появления любой конкретной выборки (как случайное событие) равна
2. Выбор без возвращения. В этом случае выбранный предмет из ящика не возвращается обратно в ящик, и следующее извлечение производится из оставшегося числа (меньшего числа) предметов. После m раз извлечений получаем строку длиною m без повторений. Количество таких строк равно
Случайный характер выбора строки понимается, как и выше, в том смысле, что все выборки данной длины (как случайное событие) имеют одну и ту же вероятность равную
-
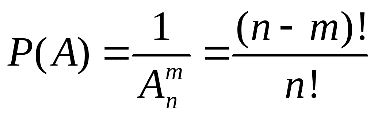
Приближенные формулы вычисления биномиальных вероятностей. Формулы Бернулли, Лапласа и Пуассона.
Формула Бернулли:
Если вероятность p наступления некоторого события испытания постоянна, то вероятность того, что данное событие наступит ровно k раз в n независимых испытаниях, равна
, где 
.Формула Лапласа:
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0
1
раз и не более k2 раз, приближенно равна
Pn = (k1 ≤ k ≤ k2) ≈ Ф(x1)-Ф(x2)
Здесь
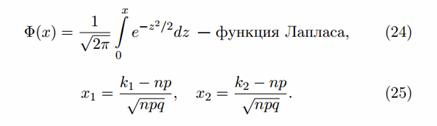
Таблица значений функции Лапласа для положительных значений x (0 ≤ x ≤ 5); для значений x> 5 полагают Ф(x) = 0,5. Для отрицательных значений x используют эту же таблицу, учитывая, что функция Лапласа нечетная: Ф(-x) = -Ф(x).
Формула Пуассона:
Пусть производится n независимых испытаний¸ в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической локальной формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала (р ≤ 0,1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное дополнение: произведение n∙p сохраняет постоянное значение, а именно, n∙p=λ.
Формула Пуассона имеет вид:
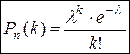, где λ=n∙p. Эта формула выражает закон Пуассона распределения вероятностей массовых (n велико) и редких (р мало) событий.10. Понятие случайной величины. Закон распределения С.В. Биномиальный закон распределения и закон распределения Пуассона.
Случайная величина — переменная, значения которой представляют собой численные исходы некоторого случайного феномена или эксперимента. Другими словами, это численное выражение результата случайного события.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.
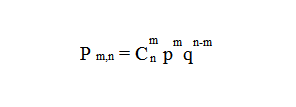
Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:
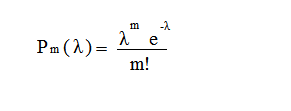
где
λ = np = const
n - число испытаний, стремящиеся к бесконечности
p - вероятность наступления события, стремящаяся к нулю
m - число появлений события А
-
Интегральная функция распределения С.В. и ее свойства
Функцией распределения или интегральной функцией распределения вероятностей называется вероятность того, что случайная величина примет значение меньшее, чем произвольное действительное число, т.е.
. 
.Свойство 1. Областью определения функции является все множество действительных чисел.
Свойство 2. Областью изменения функции является промежуток от нуля до единицы
.Свойство 3. Предел интегральной функции при
равен 1, а при 
равен 0
Свойство 4. Интегральная функция распределения является неубывающей функцией.
Свойство 5. Вероятность того, что случайная величина примет значение из промежутка определяется по формуле
.Свойство 6.
Если случайная величина непрерывна, то вероятность того, что она примет любое отдельное возможное значение равна нулю
.Свойство 7. Если случайная величина непрерывна, то имеют место равенства
.-
Плотность вероятности непрерывной С.В. и ее свойства.
Функция распределения непрерывной случайной величины является ее вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения случайной величины в небольшой окрестности той или другой точки числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины дает функция, которая называется плотностью распределения вероятности, или дифференциальной функцией распределения случайной величины.
Плотность распределения f(x) равна производной от функции распределения F(x), т. е.
Смысл плотности распределения f(x) состоит в том, что она указывает на то, как часто случайная величина X появляется в некоторой окрестности точки x при повторении опытов. Кривая, изображающая плотность распределения f(x) случайной величины, называется кривой распределения.
Свойство 1. Плотность распределения неотрицательна, т. е.
Свойство 2. Функция распределения случайной величины равна интегралу от плотности в интервале от до x, т. е.
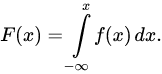
Свойство 3. Вероятность попадания непрерывной случайной величины X на участок равна интегралу от плотности распределения, взятому по этому участку, т. е.
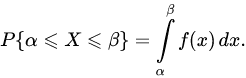
Свойство 4. Интеграл в бесконечных пределах от плотности распределения равен единице:
.-
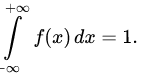Математическое ожидание С.В. и его свойства.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.
Для непрерывной случайной величины математическое ожидание
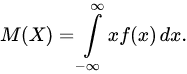
Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат отрезку ,
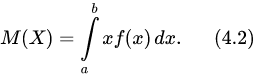
Используя функцию распределения вероятностей F(x), математическое ожидание случайной величины можно выразить так:
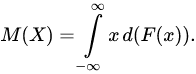
Свойства математического ожидания:
Свойство 1. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
Свойство 2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: