Файл: Лекция 1 Тема Химическая термодинамика.doc

ΔU=w, (1.6)

где ΔU=U₂ – U₁ . (1.7)

Равенство (1.6) выполнится и в том случае, если система в адиабатических условиях будет совершать работу над окружающей средой. При этом величины w и ΔU будут отрицательными. Изменение состояния по (1.7) системы может быть достигнуто не только работой в адиабатических условиях, но и другими способами. Например, изменение, эквивалентное достигнутому в опыте (а), можно получить, погружая нагретое тело в воду калориметра. При этом теплота переходит от так называемого теплового источника (нагретого тела) к воде. Однако не говорят, что в воде после этого содержится больше «теплоты» (также в опыте (а) не говорят, что в воде содержится больше «работы»). В результате этого опыта повышается температура воды и ее внутренняя энергия U.

Поскольку одно и то же изменение состояния (определяемое измерением таких свойств системы как температура, давление и объем) можно получить, совершая над системой работу или сообщая ей теплоту, то количество теплоты q может быть выражено в механических единицах. Д. Джоуль в своих опытах установил механический эквивалент теплоты, который в настоящее время можно сформулировать следующим образом: затрата 4,184 Дж механической работы над системой производит такое же изменение состояния, как и 1 калория теплоты, полученная системой извне.

Напомним, что внесистемная единица измерения теплоты калория – это количество теплоты, которое требуется для нагревания 1 г воды на 1 ^оС от 14,5 ^оС до 15,5 ^оС. Так как теплота - алгебраическая величина, то важно условиться о ее знаках. Будем принимать для q положительное значение, когда система поглощает теплоту из окружающей среды, а отрицательное значение q будет указывать на то, что система отдает теплоту окружающей среде. Если переход теплоты q к системе не сопровождается совершением работы, то вызванное этим переходом изменение внутренней энергии можно выразить следующим равенством:

ΔU=q (работа не совершается) . (1.8)

Таким образом, теплота, поглощенная закрытой системой в процессе, при котором не совершается работа, равна приросту внутренней энергии системы. Это же можно выразить по-другому: если работа не совершается, то выделившаяся теплота равна убыли внутренней энергии системы.

Экспериментально установлено, что если тело А находится в тепловом равновесии с телом С и тело В находиться в тепловом равновесии с телом С, то тела А и В находятся в тепловом равновесии друг с другом. При этом между А, В и С не будет теплообмена. Этот эмпирический факт назвали

---

нулевым законом термодинамики. Нулевой закон термодинамики можно сформулировать также следующим образом: если две системы находятся в тепловом равновесии, то их температура одинакова; если они не находятся в тепловом равновесии, то их температуры различны.

1.1.4. Первый закон термодинамики

В природе существует несколько всеобщих законов сохранения. Один из них – закон сохранения энергии. Он показывает, что энергия в изолированной системе сохраняется и может переходить из одной формы в другую в эквивалентных количествах. Энергия – это способность производить работу или переносить теплоту.

Известны две формы энергии – потенциальная и кинетическая. Видов энергии много: теплота – это кинетическая энергия структурных частиц веществ; свет – это энергия электромагнитного излучения; химическая энергия – это потенциальная энергия, возникающая вследствие различного расположения атомов и молекул относительно друг друга в различных веществах.

На рис.1.3 показаны примеры действия закона сохранения энергии. Сжимая пружину (I), мы совершаем работу, которая переходит в потенциальную – упругую энергию пружины (II). Отдавая потом эту энергию, пружина может совершить работу в виде поднятия груза m на некоторую высоту (III). Точно так же будет выглядеть процесс сжатия газа. Сжимая газ, мы увеличиваем его упругую (потенциальную) энергию, которая затем может быть использована для подъема груза m. При этом будет совершаться менее очевидный процесс – сжатие поршнем атмосферы, окружающей цилиндр. Поэтому часть упругой энергии газа будет передана атмосфере.

б F б

F m

---

а m

а






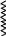
I II III I II III

Рис. 1.3. Иллюстрация закона сохранения энергии: а – стопор, б - направление движения груза m

Рассмотрим далее изолированную систему из двух тел: А – воды и В – железной плиты (рис.1.4). Допустим, что мы ставим А на горячую плиту В. Сразу же теплота от В начнет переходить к А. Когда температуры В и А станут одинаковыми (Т₃), теплообмен между ними прекратится. Они окажутся в тепловом равновесии. Так как (А+В) – изолированная система, то по закону сохранения энергии количество теплоты, которое получила при нагревании вода, должно равняться тому количеству теплоты, которое отдала плита:

q(H₂O) = – q(Fe); (1.9)

(1.10)

(1.11)

при этом T₂>T₃>T₁ .


Т₁
А

Т₃

В

Т₂

Рис.1.4. Схема теплообмена между В и А в изолированной системе (А+В)

В этих уравнениях - теплоемкость, n_i – число молей i-того компонента (воды или железа). Теплоемкостью данного вещества называется количество теплоты, которое необходимо сообщить одному молю вещества для повышения его температуры на 1 ^оС или К без изменения его фазового состояния.

В опыте с изолированной системой (А+В) горячая плита В нагрела воду А, при этом внутренняя энергия А увеличилась, а В – уменьшилось, поэтому вместо равенства (1.9) можно написать выражение (1.14):

ΔU(A) = q(H₂O), где q(H₂O)>0; (1.12)

ΔU(B) = q(Fe), где q(Fe)<0; (1.13)

---

ΔU(A+B) = ΔU(A) + ΔU(B) = 0,

откуда: ΔU(A) = – ΔU(B). (1.14)

р







р

S h₂ пар Т₃



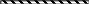
A вода T₁ h₁

B T₂

I II

Рис.1.5. Схема теплообмена между В и А в адиабатических условиях: I - начало теплообмена; II – тепловое равновесие при Т₃=373,15К (Т₂ >Т₃ ; Т₁=Т₃)

Рассмотрим далее адиабатическую систему (А+В) рис.1.5. Допустим, что закрытая система А в начале процесса (I) состоит из цилиндра с водой, сверху которой имеется невесомый поршень, перемещающийся без трения. Площадь поршня равна S. При контакте А с более нагретой системой В (металлическая плита) теплота от В будет переходить к А. В результате вода будет переходить в парообразное состояние при Т₁=373,15 К. Все параметры систем А и В (размеры, масса, Т₂) подобраны так, чтобы в конце процесса парообразования конечная температура А и В (Т₃) осталась равной Т₁(II). Для рассматриваемого случая мы можем повторить формулу (1.9):

q(H₂O) = – q(Fe);

а вот можем ли мы написать для этого случая формулу (1.12)? Оказывается, не можем, так как при переходе воды в пар исходный объем A, равный h₁S (V₁) увеличивается, и поршень, двигаясь вверх, совершает работу, преодолевая атмосферное давление:

p=F/S, (1.15)

где F – сила, действующая на поршень, которую можно выразить следующим образом:

F = pS. (1.16)

Сила F против атмосферного давления действует на расстоянии h₂-h₁. Их произведение даст работу, совершаемую паром:

w = pS(h₂ – h₁) = p(V₂ – V₁) = pΔV, (1.17)

где Sh₂ – объем пара в равновесии II. Так как система А совершает работу (1.17), то ее внутренняя энергия уменьшается на эту величину. И правильно будет вместо (1.12) написать:

ΔU(A) = q(H₂O) – pΔV (1.18)

или

ΔU(A) = q(H₂O) – w. (1.19)

Работа системы А против атмосферного давления идет на увеличение упругой энергии атмосферы (по аналогии с опытом рис.1.3). Если цилиндр с паром (А) поставить на холодную плиту (В), то произойдет обратный процесс – конденсация пара, атмосфера расширится на ΔV и отдаст энергию pΔV сжимаемой системе (А).

---

Формулу (1.9) для различных процессов можно записать в общем виде:

∆U = q + w, (1.20)

где все величины могут иметь различные знаки – положительные и отрицательные в зависимости от того, какой процесс происходит с системой. Формула (1.20) – это математическая запись первого закона термодинамики, который подчеркивает, что внутренняя энергия системы может изменяться – убывать или возрастать за счет отдачи или приобретения теплоты и совершения системой или над системой работы. Это различные проявления закона сохранения энергии. Первый закон термодинамики иногда формулируюттак: энергию можно превратить из одной формы в другую, но ее нельзя создать или уничтожить, и общее количество энергии в изолированной системе постоянно.

Формула (1.20) выведена при рассмотрении частного случая. Можно показать ее вывод в общем случае, опираясь на формулы (1.6) и (1.8). Для этого рассмотрим переход закрытой системы из состояния (1) в состояние (2), сопровождающийся совершением системой работы (или над ней) в ходе которого система, приведенная в контакт с тепловым источником, приобретает (или теряет) теплоту. Применяя уравнение (1.6) к системе и тепловому источнику, получим:

(U₂ – U₁) + (U₂' – U₁') = w₁, (1.21)

где (U₂ – U₁) – изменение внутренней энергии системы, а (U₂' – U₁') – изменение внутренней энергии теплового источника. Второе слагаемое левой части уравнения (1.21) равно теплоте, отданной тепловым источником: (U₂' – U₁')= – q. Тогда уравнение (1.21) приобретает вид:

U₂ – U₁ = ∆U = w+q , (1.22)

Видно, что мы получили выражение первого закона термодинамики. Следует подчеркнуть, что этот закон позволяет определить только изменение внутренней энергии, но не абсолютную ее величину. О внутренней энергии в настоящее время можно сказать следующее: все вещества только потому что существуют обладают энергией. Эта энергия складывается из энергии взаимодействий между собой атомов, молекул и ионов, то есть из энергии химических связей, а также из энергии их теплового движения. Сколько этой энергии в веществе мы не знаем. Но чем больше вещества, тем больше энергии. Эту энергию назвали внутренней энергией. Другие формы энергии, как, например, ядерная энергия, в химических системах чаще всего не учитываются и в значение их внутренней энергии не входят. Кроме того, при термодинамическом рассмотрении систем предполагается, что они находятся в состоянии относительного покоя (Е

---