ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 282
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
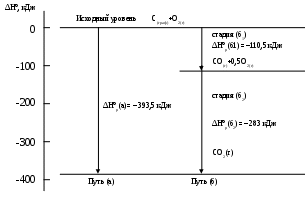
=0). Нижний уровень диаграммы соответствует значению энтальпии образования конечного продукта реакции. Такое расположение исходного и конечного уровней энтальпийных диаграмм характерно для экзотермических процессов. В случае эндотермических процессов исходный уровень будет располагаться ниже конечного уровня, соответствующего энтальпии образования продукта.
1.2.4. Теплоты растворения
При растворении веществ теплота может поглощаться или выделяться. В общем случае количество теплоты растворения зависит от концентрации полученного раствора. Интегральная теплота растворения определяется как изменение энтальпии при растворении одного моля вещества в n молях растворителя. Процесс растворения можно представить в виде химического уравнения:
НС1(г) +5Н2О(ж) = НС1 в 5Н2О; ΔН°р-я = – 64,05 кДж , (1.62)
где «НС1 в 5Н2О» означает раствор 1 моля НС1 в 5 молях Н2О.
Зависимость интегральных теплот растворения NaCl, NaOH и НCl от количества воды показана на рис. 1.10.
В записях, подобных (1.62), употребляется также символ «aq»,
обозначающий водный раствор, разбавленный настолько, что
дальнейшее разбавление не сопровождается тепловым эффектом. Например:
НС1 (г) + aq = HCl(aq) , ∆Нор-я = – 75,14 кДж . (1.63)
Когда растворяемое вещество и растворитель химически
подобны и при растворении не возникает осложнений, связанных с
ионизацией или сольватацией, теплоту растворения можно считать
приблизительно равной теплоте плавления растворяемого вещества. Однако чаще всего указанные осложнения при растворении бывают. Например, в кристаллической решетке хлорида натрия положительные ионы натрия и отрицательные ионы хлора испытывают сильное взаимное притяжение. Энергия, необходимая для их разделения, настолько велика, что такие неполярные
растворители как бензол и четыреххлористый углерод не
растворяют хлорид натрия. Растворители подобные воде, имеющие
большие значения диэлектрической постоянной и дипольных
моментов молекул, растворяют ионные кристаллы, и NaCl, в
частности. Их молекулы сильно притягиваются как к ионам натрия
так и к ионам хлора. В результате происходит сольватация (образование вокруг ионов оболочек из полярных молекул воды, которые называют в общем случае сольватными) ионов, которая сопровождается значительным уменьшением энергии системы (выделением энергии). Если энергия, требуемая для отрыва ионов от кристалла, близка по значению к энергии сольватации, как, например, в случае растворения NaCl в воде,то значение ∆Нр-я для суммарного процесса близко к нулю. При растворении NaCl в воде при 298К наблюдается лишь небольшое охлаждение раствора, а величина ∆Нр-я
положительна. В случае растворения веществ в воде их сольватация
называется гидратацией.
+4
+2 NaCl
0
-2
-4
-6
-8 NaOH
10
12
14
16 HCl
18
0 5 10 15 20 25 30 35 40 45
Число молей Н2О на 1 моль растворенного вещества

Рис.1.10.Интегральные теплоты растворения соединений при 298 К
Интегральная теплота разбавления раствора от моляльности b1 до моляльности b2 определяется как количество теплоты, которое поглощается или выделяется при разбавлении некоторого объема раствора с концентрацией b1, содержащего 1 моль растворенного вещества, чистым растворителем до концентрации b2.
Интегральные теплоты растворения, теплоты разбавления и теплоты реакций в растворах могут быть рассчитаны из табулированных значений теплот образования веществ в растворенном состоянии. В таких расчетах можно пренебречь энтальпией образования воды, если в обе части уравнения химической реакции входит одинаковое число молей воды. Энтальпия образования воды в водном растворе принимается равной энтальпии образования чистой воды. Это допущение так же произвольно, как и приравнивание к нулю энтальпий образования элементов.
ЛЕКЦИЯ 4 1.2.5. Зависимость тепловых эффектов химических
реакций и процессов от температуры
Уравнение химической реакции в общем виде можно представить следующим образом:
1А1 + 2А2 = 3А3 + 4А4,
где i – стехиометрические коэффициенты, А1 и А2 – реагенты, А3 и А4 – продукты реакции. Тогда изменение энтальпии данной реакции (∆Н) при соответствующей температуре можно вычислить по (1.56), вычитая сумму энтальпий исходных веществ из суммы энтальпий продуктов реакции (в частности, при стандартной температуре) –
,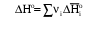 (1.64)
(1.64)
где 3 и 4 положительны, а 1 и 2 отрицательны. Поскольку энтальпии химических реакций зависят от температуры, то скорость изменения с изменением температуры можно вычислить, дифференцируя уравнение (1.64) по температуре при постоянном давлении:

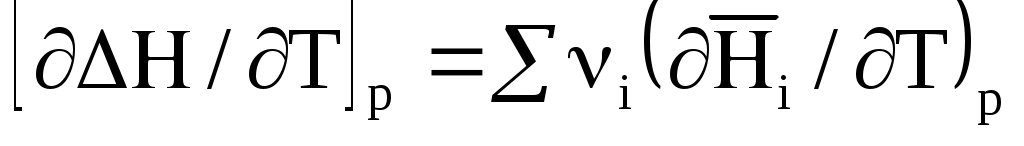 . (1.65)
. (1.65)
Учитывая по (1.40), что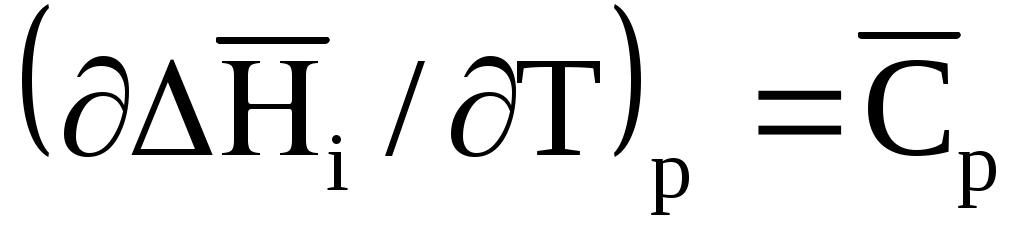 , вместо (1.65) получим:
, вместо (1.65) получим:
 . (1.66)
. (1.66)
Полученное уравнение называется уравнением Кирхгофа. Оно показывает, что при постоянном давлении изменение энтальпии реакции в результате повышения температуры реакционной системы на один градус равно изменению ее теплоемкости.
Уравнение (1.66) можно проинтегрировать от Т1 до Т2 и получить соотношение между изменениями энтальпии реакции при указанных температурах:
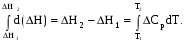 (1.67)
(1.67)
Это уравнение позволяет вычислить ΔΗ реакции при заданной температуре, если известны ΔΗ реакции при другой температуре и значения реагентов и продуктов реакции в промежуточной области температур. Им удобно пользоваться в тех случаях, когда известны эмпирические зависимости Ср,i от температуры – (1.50). Уравнение (1.67) справедливо только при условии, что в области температур от Т1 до Т2 не происходит фазовых превращений. Для учета изменений энтальпии в случае фазовых превращений (∆Нф – плавления, испарения, кристаллизации, конденсации)в промежутке ΔΤ в уравнение (1.67) необходимо вводить дополнительные члены:
реагентов и продуктов реакции в промежуточной области температур. Им удобно пользоваться в тех случаях, когда известны эмпирические зависимости Ср,i от температуры – (1.50). Уравнение (1.67) справедливо только при условии, что в области температур от Т1 до Т2 не происходит фазовых превращений. Для учета изменений энтальпии в случае фазовых превращений (∆Нф – плавления, испарения, кристаллизации, конденсации)в промежутке ΔΤ в уравнение (1.67) необходимо вводить дополнительные члены:
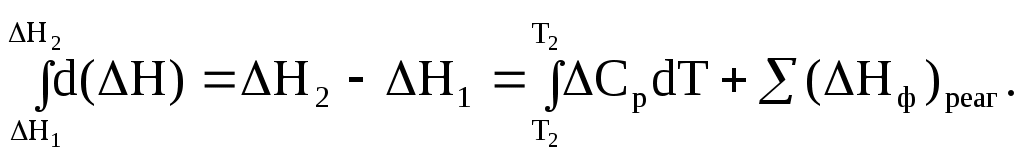 (1.68)
(1.68)
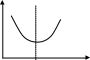
Если теплоемкости продуктов реакции больше теплоемкостей исходных веществ, то для экзотермической реакции ( тепловой эффект реакции с повышением температуры падает, а для эндотермической реакции ( - растет. Если Ср, то наблюдаются обратные зависимости. В случае равенства теплоемкостей продуктов и исходных веществ тепловой эффект реакции не зависит от температуры. В общем случае зависимости энтальпий реакций от Т могут иметь экстремумы в точках, где теплоемкости продуктов и исходных веществ равны, например, как показано на рис. 1.11.
 Ср,i
Ср,i
исходные
вещества
продукты продукты
Т1 Т Т1 Т
Рис.1.11. Общий вид зависимостей от температуры Ср,i реагентов
и продуктов и ΔН реакции
Так как на кривых ∆Н = f(Т) могут быть экстремумы, то их нельзя экстраполировать за пределы опытных данных.
При решении уравнения (1.67) чаще всего берут Т1=298 К, а изменение энтальпии реакции вычисляют по закону Гесса, используя табличные значения энтальпий образования веществ. Если теплоемкости в рассматриваемом интервале температур постоянны, то получают:
Н2 = H1 + Cр (T2 - Т1). (1.69)
Например, вычислим, какое количество теплоты выделится при замерзании одного моля переохлажденной воды при постоянном давлении 1 атм и температуре 263 К:
Н2О(ж) → Н2О(к).
По табличным данным имеем следующие значения: (Н2О) (кристаллизации) при 273К = – 6,009 кДж/моль,
(Н2О) (кристаллизации) при 273К = – 6,009 кДж/моль,  (Н2О(к)) = 36,9Дж/(моль∙К),
(Н2О(к)) = 36,9Дж/(моль∙К),  (Н2О(ж)) = 75,31 Дж/(моль∙К). Для рассматриваемого процесса в соответствии с (1.67) необходимо вычислить
(Н2О(ж)) = 75,31 Дж/(моль∙К). Для рассматриваемого процесса в соответствии с (1.67) необходимо вычислить  при Т2=263 К:
при Т2=263 К:


Рис 1.9. Энтальпийная диаграмма образования оксида углеродаIV
1.2.4. Теплоты растворения
При растворении веществ теплота может поглощаться или выделяться. В общем случае количество теплоты растворения зависит от концентрации полученного раствора. Интегральная теплота растворения определяется как изменение энтальпии при растворении одного моля вещества в n молях растворителя. Процесс растворения можно представить в виде химического уравнения:
НС1(г) +5Н2О(ж) = НС1 в 5Н2О; ΔН°р-я = – 64,05 кДж , (1.62)
где «НС1 в 5Н2О» означает раствор 1 моля НС1 в 5 молях Н2О.
Зависимость интегральных теплот растворения NaCl, NaOH и НCl от количества воды показана на рис. 1.10.
В записях, подобных (1.62), употребляется также символ «aq»,
обозначающий водный раствор, разбавленный настолько, что
дальнейшее разбавление не сопровождается тепловым эффектом. Например:
НС1 (г) + aq = HCl(aq) , ∆Нор-я = – 75,14 кДж . (1.63)
Когда растворяемое вещество и растворитель химически
подобны и при растворении не возникает осложнений, связанных с
ионизацией или сольватацией, теплоту растворения можно считать
приблизительно равной теплоте плавления растворяемого вещества. Однако чаще всего указанные осложнения при растворении бывают. Например, в кристаллической решетке хлорида натрия положительные ионы натрия и отрицательные ионы хлора испытывают сильное взаимное притяжение. Энергия, необходимая для их разделения, настолько велика, что такие неполярные
растворители как бензол и четыреххлористый углерод не
растворяют хлорид натрия. Растворители подобные воде, имеющие
большие значения диэлектрической постоянной и дипольных
моментов молекул, растворяют ионные кристаллы, и NaCl, в
частности. Их молекулы сильно притягиваются как к ионам натрия
так и к ионам хлора. В результате происходит сольватация (образование вокруг ионов оболочек из полярных молекул воды, которые называют в общем случае сольватными) ионов, которая сопровождается значительным уменьшением энергии системы (выделением энергии). Если энергия, требуемая для отрыва ионов от кристалла, близка по значению к энергии сольватации, как, например, в случае растворения NaCl в воде,то значение ∆Нр-я для суммарного процесса близко к нулю. При растворении NaCl в воде при 298К наблюдается лишь небольшое охлаждение раствора, а величина ∆Нр-я
положительна. В случае растворения веществ в воде их сольватация
называется гидратацией.
+4
+2 NaCl
0
-2
-4
-6
-8 NaOH
10
12
14
16 HCl
18
0 5 10 15 20 25 30 35 40 45
Число молей Н2О на 1 моль растворенного вещества

Рис.1.10.Интегральные теплоты растворения соединений при 298 К
Интегральная теплота разбавления раствора от моляльности b1 до моляльности b2 определяется как количество теплоты, которое поглощается или выделяется при разбавлении некоторого объема раствора с концентрацией b1, содержащего 1 моль растворенного вещества, чистым растворителем до концентрации b2.
Интегральные теплоты растворения, теплоты разбавления и теплоты реакций в растворах могут быть рассчитаны из табулированных значений теплот образования веществ в растворенном состоянии. В таких расчетах можно пренебречь энтальпией образования воды, если в обе части уравнения химической реакции входит одинаковое число молей воды. Энтальпия образования воды в водном растворе принимается равной энтальпии образования чистой воды. Это допущение так же произвольно, как и приравнивание к нулю энтальпий образования элементов.
ЛЕКЦИЯ 4 1.2.5. Зависимость тепловых эффектов химических
реакций и процессов от температуры
Уравнение химической реакции в общем виде можно представить следующим образом:
1А1 + 2А2 = 3А3 + 4А4,
где i – стехиометрические коэффициенты, А1 и А2 – реагенты, А3 и А4 – продукты реакции. Тогда изменение энтальпии данной реакции (∆Н) при соответствующей температуре можно вычислить по (1.56), вычитая сумму энтальпий исходных веществ из суммы энтальпий продуктов реакции (в частности, при стандартной температуре) –
,
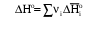 (1.64)
(1.64)где 3 и 4 положительны, а 1 и 2 отрицательны. Поскольку энтальпии химических реакций зависят от температуры, то скорость изменения с изменением температуры можно вычислить, дифференцируя уравнение (1.64) по температуре при постоянном давлении:
Учитывая по (1.40), что
Полученное уравнение называется уравнением Кирхгофа. Оно показывает, что при постоянном давлении изменение энтальпии реакции в результате повышения температуры реакционной системы на один градус равно изменению ее теплоемкости.
Уравнение (1.66) можно проинтегрировать от Т1 до Т2 и получить соотношение между изменениями энтальпии реакции при указанных температурах:
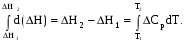 (1.67)
(1.67)Это уравнение позволяет вычислить ΔΗ реакции при заданной температуре, если известны ΔΗ реакции при другой температуре и значения
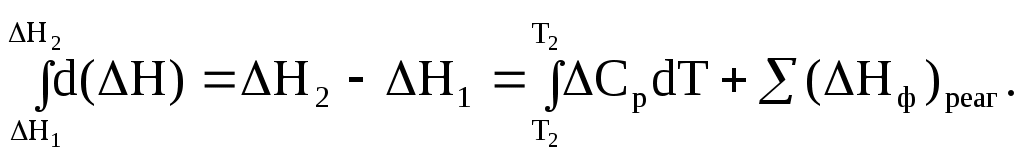 (1.68)
(1.68)Если теплоемкости продуктов реакции больше теплоемкостей исходных веществ, то для экзотермической реакции ( тепловой эффект реакции с повышением температуры падает, а для эндотермической реакции ( - растет. Если Ср, то наблюдаются обратные зависимости. В случае равенства теплоемкостей продуктов и исходных веществ тепловой эффект реакции не зависит от температуры. В общем случае зависимости энтальпий реакций от Т могут иметь экстремумы в точках, где теплоемкости продуктов и исходных веществ равны, например, как показано на рис. 1.11.

 Ср,i
Ср,i исходные
вещества
продукты продукты
Т1 Т Т1 Т
Рис.1.11. Общий вид зависимостей от температуры Ср,i реагентов
и продуктов и ΔН реакции
Так как на кривых ∆Н = f(Т) могут быть экстремумы, то их нельзя экстраполировать за пределы опытных данных.
При решении уравнения (1.67) чаще всего берут Т1=298 К, а изменение энтальпии реакции вычисляют по закону Гесса, используя табличные значения энтальпий образования веществ. Если теплоемкости в рассматриваемом интервале температур постоянны, то получают:
Н2 = H1 + Cр (T2 - Т1). (1.69)
Например, вычислим, какое количество теплоты выделится при замерзании одного моля переохлажденной воды при постоянном давлении 1 атм и температуре 263 К:
Н2О(ж) → Н2О(к).
По табличным данным имеем следующие значения:
