Файл: Лекция 1 Тема Химическая термодинамика.doc

Рис. 3.2. Распределение молекул газа по энергиям

Величины k и А уравнения (3.5) оказываются одной размерности, т.е. А тоже константа скорости и отражает частоту столкновений частиц. Расчетная частота столкновений молекул газа обычно больше, чем А, определенное по экспериментальным данным в соответствии с (3.5). Возможное объяснение этого состоит в том, что эффективными являются не только соударения частиц с достаточной энергией, но и необходимо еще, чтобы они были соответственно сориентированы в пространстве по отношению друг к другу. Например, в реакции



ориентация частиц (1) более благоприятна для взаимодействия, чем ориентация (2):

Cl

→ ←H – C – Cl (1);

Cl
H

→ ← Cl – C – Cl (2),

Cl

(где и обозначают частицы, имеющие неспаренные электроны, т.е. это радикалы). Иными словами, множитель А в (3.5) должен включать в себя наряду с Z по (3.8) стерический фактор P (имеющий значение от 0 до 1), соответствующий той части сталкивающихся частиц, которые имеют необходимую взаимную ориентацию (А=РZ). Поэтому считают, что множитель А представляет собой частоту соударений активных частиц, ориентированных определенным образом.

Теория соударений была разработана для бимолекулярных реакций (с участием в каждом столкновении двух частиц) в газовой фазе. Однако, оказалось, что ее можно использовать и для реакций в растворах. В этом случае молекулы растворителя препятствуют столкновениям частиц реагентов с такой же частотой, как в газах, но зато после неэффективного соударения частицы не расходятся далеко и могут сталкиваться повторно. Такие повторные столкновения между частицами могут оказаться эффективными. Было показано, что скорость некоторых реакций одинакова и в газовой фазе, и в растворах.

---

Итак, теория бинарных соударений утверждает, что для химического превращения взаимодействующие частицы должны: I. столкнуться; II. иметь благоприятную взаимную ориентацию; III. обладать достаточной энергией. В рамках этой теории уравнение Аррениуса (3.5) выведено теоретически.

Теория переходного состояния

Эта теория рассматривает процесс соударения частиц в деталях. По ней в момент соударения частиц они сближаются и между их электронными облаками нарастает взаимное отталкивание. Скорость движения частиц при этом уменьшается, а кинетическая энергия переходит в потенциальную. Если кинетическая энергия частиц была недостаточной, то они остановятся раньше, чем их электронные облака перекроются, и тогда частицы, не взаимодействуя друг с другом химически, расходятся. Если сталкиваются две активные частицы (с энергией ≥Е (рис. 3.2)), то они могут преодолеть отталкивание между электронными облаками и близко подойти друг к другу. В результате перекрывания их электронных облаков создаются условия для перераспределения электронов с разрывом старых химических связей и образованием новых, т.е. условия для протекания химической реакции.

В качестве примера на рис.3.3 показано изменение потенциальной энергии одного эффективного соударения метильного радикала и молекулы хлороводорода:

(3.9)

Ось абсцисс диаграммы – это координата реакции r, показывающая степень развития процесса взаимодействия частиц от начального состояния до продуктов. После столкновения частиц их потенциальная энергия возрастает до максимума, которому соответствует образование, состоящее из атомных ядер и связывающих электронов и называемое активированным комплексом. В таком комплексе начинают образовываться новые связи с одновременным разрывом старых связей (т.е. перераспределяются электроны между атомами); в нем как бы объединены «полуразрушенные» частицы реагентов и «полуобразовавшиеся» частицы продуктов.

AK

H₃C·······H·······Cl

---

П

P

E

E_A

r

---

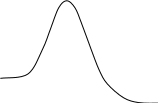
Рис. 3.3. Диаграмма потенциальной энергии для

единичного столкновения реагентов Р:

АК – активированный комплекс;

П - продукты

Активированный комплекс (АК) для рассмотренной реакции можно представить следующим образом: [Н₃С···Н···Сl ]. В общем виде взаимодействие молекул А₂ и В₂ будет протекать по уравнению:


реагенты активированный продукты

(начальное состояние) комплекс (конечное состояние)

Разность потенциальной энергии активированного комплекса и реагентов называют энергией активации Е_А.

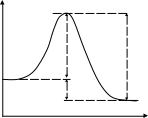
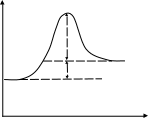
Если в реакции (3.9) будет участвовать по одному молю частиц реагентов, то стандартным условиям будет соответствовать диаграмма, представленная на рис. 3.4а, которую называют энтальпийным или энергетическим профилем реакции. Она показывает соотношение между

а) б)

AK АК







Е_а

П

Р Р

П



r r

Рис. 3.4. Энтальпийные профили реакций

стандартными энтальпиями 1 моля реагентов, активированных комплексов и продуктов. и на рис.3.4.а представляют энергии активации прямой и обратной реакций (Е_а для каждой реакции величина постоянная), а − стандартная энтальпия реакции (3.9). Видно, что

---

а знак указывает, что реакция (3.9) экзотермическая ( <0). В случае эндотермических реакций энтальпийный профиль будет иметь вид, подобный кривой рис.3.4б, этих реакций положительно. Следует отметить, что теория переходного состояния применима как к реакциям в газах, так и к реакциям в растворах.

ЛЕКЦИЯ 13 3.4. СЛОЖНЫЕ ХИМИЧЕСКИЕ РЕАКЦИИ

В основе кинетики сложных химических реакций лежит принцип независимости реакций, согласно которому: если в системе протекает несколько реакций, то каждая из них протекает независимо от других, так что общее изменение в системе равно сумме этих независимых изменений.

В последовательных реакциях продукт одной реакции является исходным веществом для другой реакции. Рассмотрим схему простейшего примера:

А = В = С,

в котором вещество В является промежуточным. Согласно кинетическим кривым рис.3.5, концентрация исходного вещества снижается, а продукта - увеличивается. Концентрация В вначале увеличивается, достигая максимума, а затем уменьшается, так как расход вещества В не компенсируется его образованием из вещества А.



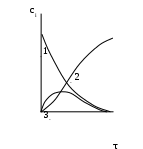
Рис. 3.5. Зависимость концентрации веществ от времени (кинетические кривые) при протекании сложной реакции, состоящей из двух последовательных стадий: 1 – исходное вещество; 2 – продукт реакции; 3 – промежуточное вещество

Если константы скоростей отдельных стадий близки по значениям, то константа скорости суммарной реакции будет равна их величине: k₁ ≈ k₂ ≈ k_i ≈ ≈ k. Если же константы скоростей отдельных стадий отличаются друг от друга значительно, то скорость суммарной реакции будет определяться самой медленно идущей стадией: k = k_min.

Примером последовательно идущих реакций может служить процесс образования оксида азота IV из азота и кислорода воздуха в условиях работы двигателей внутреннего сгорания (автомобилей). Вначале при высокой температуре горения топлива образуется оксид азотаII:

N₂ + O₂ = 2NO,

который затем частично окисляется кислородом до оксида азотаIV:

---