Файл: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 110
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
vi и v4. Число таких столкновений в единицу времени в единице объема газа должно быть пропорционально числу молекул со скоростями вблизи v1 и v2, то есть произведению n(v1)·n(v2). Рассмотрим далее процесс соударения, являющийся обратным данному. При этом скорости молекул изменяются от значений v3 и v4 до значений v1 и v2. Число таких соударений в единицу времени в объеме пропорционально количеству молекул со скоростями вблизи v3 и v4, то есть n(v3)·n(v4).
В силу предположения о молекулярном хаосе и предположения о том, что число молекул с данными значениями скорости не изменяется процессами молекулярных столкновений в газе, находящемся в стационарном состоянии, можно считать, что число молекул, у которых скорости изменяются от значений v1 и v2 до значений v3 и v4, равно числу молекул, у которых скорости изменяются от v3 и v4 до v1 и v2. Отсюда следует, что
Равенство (3.14) выражает баланс частиц, получающих и теряющих соответствующую скорость, причем в процессе таких упругих соударений энергия молекул сохраняется (m0 — масса молекулы):
Равенства (3.10), (3.14) и (3.15) представляют совокупности условий, которым должна удовлетворять искомая функция распределения.
Используя (3.15), выразим v4 через v1, v2, v3:
Функциональные уравнения (3.14) и (3.16) легко превратить в простое дифференциальное уравнение. Взяв логарифм от (3.14), имеем
Продифференцируем (3.17) по аргументу v1:
Аналогично
Учитывая выражение (3.16), находим
Подставляя (3.20) в правые части соотношений (3.18) и (3.19), приходим к равенству
При этом мы должны помнить, что это равенство справедливо при совершенно произвольных значениях v1, v2, которые являются независимыми переменными. Это значит, что равенство (3.21) должно иметь место при совершенно произвольных значениях скоростей, поэтому оно может быть выполнено только тогда, когда правая и левая части (3.21) равны некоторой постоянной (которую мы обозначим через ( –α)):
где переменная v может принимать значения v1, v2 или любое иное. Разделяя переменные, записываем (3.22) в виде
Интегрируя (3.23), находим
где А — постоянная интегрирования. Из физических соображений очевидно, что
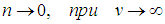
Большие скорости молекул маловероятны. Поэтому коэффициент α > 0. Постоянная А определяется из условия нормировки (3.10):
Далее будет показано, что параметр α должен быть связан с абсолютной температурой T соотношением
С учетом (3.26) из (3.24) получим
Формула (3.27) и представляет собой искомое распределение молекул по скоростям.
Учитывая, что n(v) зависит только от модуля скорости, а их направления равновероятны, можно ввести функцию распределения f(v) молекул по абсолютной величине скорости. Для этого надо проинтегрировать выражение (3.13) по углам, что дает
Отсюда и из (3.27) следует выражение для функции распределения Максвелла для модуля вектора скорости f(v):
Величина f(v)dv есть вероятность найти частицу с модулем скорости, лежащим в интервале от v до v + dv. Условие нормировки распределения f(v) принимает теперь вид
В этом разделе приводятся некоторые следствия, вытекающие из формул (3.29
) и (3.30
). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К.
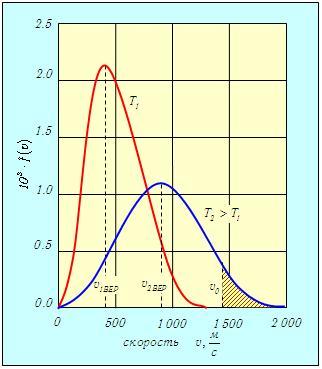
Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T1 = 300 К и T2 = 1 300 К
Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю
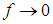
то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.
Ее можно найти, решая уравнение
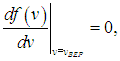
откуда следует, что
Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:
В силу предположения о молекулярном хаосе и предположения о том, что число молекул с данными значениями скорости не изменяется процессами молекулярных столкновений в газе, находящемся в стационарном состоянии, можно считать, что число молекул, у которых скорости изменяются от значений v1 и v2 до значений v3 и v4, равно числу молекул, у которых скорости изменяются от v3 и v4 до v1 и v2. Отсюда следует, что
| |  | (3.14) |
Равенство (3.14) выражает баланс частиц, получающих и теряющих соответствующую скорость, причем в процессе таких упругих соударений энергия молекул сохраняется (m0 — масса молекулы):
| |  | (3.15) |
Равенства (3.10), (3.14) и (3.15) представляют совокупности условий, которым должна удовлетворять искомая функция распределения.
Используя (3.15), выразим v4 через v1, v2, v3:
| |  | (3.16) |
Функциональные уравнения (3.14) и (3.16) легко превратить в простое дифференциальное уравнение. Взяв логарифм от (3.14), имеем
| |  | (3.17) |
Продифференцируем (3.17) по аргументу v1:
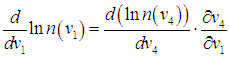| |  | (3.18) |
Аналогично
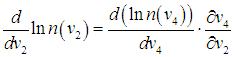| |  | (3.19) |
Учитывая выражение (3.16), находим
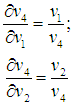| |  | (3.20) |
Подставляя (3.20) в правые части соотношений (3.18) и (3.19), приходим к равенству
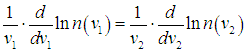| |  | (3.21) |
При этом мы должны помнить, что это равенство справедливо при совершенно произвольных значениях v1, v2, которые являются независимыми переменными. Это значит, что равенство (3.21) должно иметь место при совершенно произвольных значениях скоростей, поэтому оно может быть выполнено только тогда, когда правая и левая части (3.21) равны некоторой постоянной (которую мы обозначим через ( –α)):
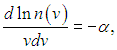| |  | (3.22) |
где переменная v может принимать значения v1, v2 или любое иное. Разделяя переменные, записываем (3.22) в виде
| |  | (3.23) |
Интегрируя (3.23), находим
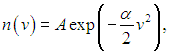| |  | (3.24) |
где А — постоянная интегрирования. Из физических соображений очевидно, что
Большие скорости молекул маловероятны. Поэтому коэффициент α > 0. Постоянная А определяется из условия нормировки (3.10):
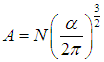| |  | (3.25) |
Далее будет показано, что параметр α должен быть связан с абсолютной температурой T соотношением
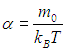| |  | (3.26) |
С учетом (3.26) из (3.24) получим
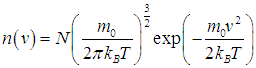| |  | (3.27) |
Формула (3.27) и представляет собой искомое распределение молекул по скоростям.
Учитывая, что n(v) зависит только от модуля скорости, а их направления равновероятны, можно ввести функцию распределения f(v) молекул по абсолютной величине скорости. Для этого надо проинтегрировать выражение (3.13) по углам, что дает
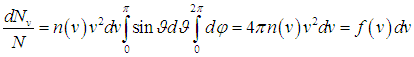| |  | (3.28) |
Отсюда и из (3.27) следует выражение для функции распределения Максвелла для модуля вектора скорости f(v):
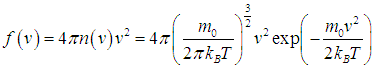| |  | (3.29) |
Величина f(v)dv есть вероятность найти частицу с модулем скорости, лежащим в интервале от v до v + dv. Условие нормировки распределения f(v) принимает теперь вид
| |  |
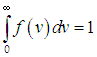3.3. Характерные скорости молекул
В этом разделе приводятся некоторые следствия, вытекающие из формул (3.29
) и (3.30 ). В качестве примера на рис. 3.3 изображены две кривые, соответствующие распределениям f(v) молекул кислорода O2 по абсолютным величинам скоростей при температурах Т1 = 300 К и Т2 = 1 300 К. Рис. 3.3. Распределение молекул кислорода по скоростям при разных температурах T1 = 300 К и T2 = 1 300 К
Наиболее вероятная скорость. При бесконечно малых и неограниченно больших значениях скоростей функция распределения стремится к нулю
то есть такие предельные значения скоростей маловероятны в системе. Следовательно, при каком-то значении скорости функция f(v) достигает своего максимума.
| Наиболее вероятная скорость vВЕР — это скорость, отвечающая максимальному значению функции распределения. |
Ее можно найти, решая уравнение
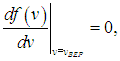
откуда следует, что
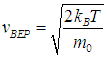| |  | (3.31) |
Иными словами, наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул. В этой точке f(v) принимает максимальное значение:
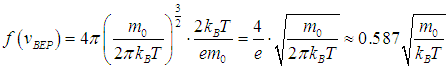| |  | (3.32) |