ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 218
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Жеке сутартқыш ұңғымалары келесі түрде есептеледі:
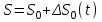, мұндағы S сутартқышты пайдаланудың аяқталу мерзімінде жобалық пайдалану өнімі Qэ кезінде ұңғымадағы су деңгейінің есептік төмендеуі;
So тәжірибелік сутарту аяқталған кезеңде берілген жобалық шығым үшін төмендеуге өнімнің тәуелділігі қисығы бойынша анықталатын, есептік ұңғымада су деңгейінің төмендеуі;
So(t) пайдаланулық қорлар есептелген мерзім соңына дейін тәжірибелік сутарту аяқталғаннан кейінгі уақыт ішінде пайдаланулық өніммен жұмыс жасайтын ұңғымадағы су деңгейінің қосымша төмендеуі.
Өнімнің қисықтарын экстраполяциялау тәсілі өнім мен төмендеу арасындағы тәуелділікті анықтауда, өнім қисығының теңдеуін құрастыруда және Q = f (S) графигін тұрғызуда қолданылады. Бұл тәуелділікті анықтай отырып экстраполяциялау жолымен сутарту кезіндегіден үлкен төмендеулер кезінде пайдаланудың жаңадан берілген шарттарына (жағдайларына) қатысты ұңғыманың өнімін болжауға болады. Бұл өнім пайдаланулық қорлар ретінде көрсетіледі. Экстраполяция не аналитикалық, не графикалық тәсілмен жүргізіледі.
Грунтты сулардың өнімінің қисықтарын экстраполяциялау S төмендеуі кезінде Q еркін шығыны үшін Дюпюи теңдеуінен шығарылады:
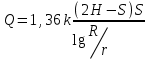, немесе Sx төмендеуі кезіндесол ұңғыманың табылатын Qx шығыны үшін:
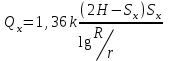. (7.48) теңдеуін (7.49) теңдеуіне бөле отырып аламыз
; 
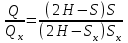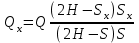, мұндағы Qx төмендеу S кезіндегі табылатын өнім;
Sx жобалық төмендеу;
Q және S сутарту кезінде алынған өнім мен деңгейдің төмендеуі;
Н сулы горизонт қалыңдығы.
Басқа мысал қарастырайық. Дюпюи теңдеуіне (7.48) сәйкес жақшаларды ашып аламыз
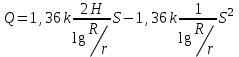. Тұрақты шамаларды
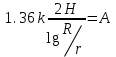және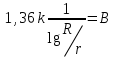 
, арқылы белгілей отырып, (7.51)-ден қисық өнім теңдеуін аламыз
Q = AS BS2,
ол бойынша бастапқы өнімді анықтауға болады
Qx = ASx BSx2 .
А және В параметрлері сутарту мәліметтері бойынша екі теңдеу жүйесін шешу жолымен екі төмендеуде орналасқан.
Арынды сулар өнімінің түзу сызықты, параболалы, логарифмдік немесе дәрежелік сипатқа ие болатын қисықтарын экстрополяциялау кезінде Дюпюи, Каллер, Альтовский, Смрекер және т.б. теңдеулері қолданылады.
Дюпюи теңдеуі. Арынды сулы горизонтта жатқан ұңғыманың шығыны
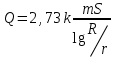. Осы ұңғыманың Qx өнімі Sx төмендеулері кезінде анықталады
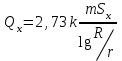. (7.55) теңдеуін (7.56) теңдеуіне бөліп, аламыз
, 
, 
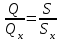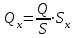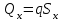, мұндағы q ұңғыманың меншікті өнімі.
Алынған теңдеу координаталардың басы арқылы өтетін түзу ретінде көрінеді (7.22-сурет). Экстраполяция Q-дың S-қа тәуелділігі түзусызықты болса және түзу координаттар басы арқылы өтсе ғана Дюпюи теңдеуімен жүргізіледі. Өнімді Sx ≤ (1,5 ч 1,75) Smax кезінде есептеу жүргізілуі тиіс, Расчет дебита допускается производить при Sx ≤ (1,5 ч 1,75) Smax, мұндағы Smax тәжірибелік сутарту кезінде алынған максималды төмендеу.
S = aQ + вQ2 ,
мұндағы Q - S төмендеу кезіндегі ұңғыманың өнімі;
а, в сутарту мәліметтері бойынша анықталған параметрлер.
(7.58) теңдеуін түзу сызықты түрге келтіру үшін Q-ға бөлеміз
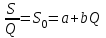, мұндағы S0 – меншікті төмендеу (бірлік шығынға келетін төмендеу).
Алынған (7.58), (7.59) тәуелділіктері бойынша Келлер теңдеуін графикалық түрде көрсетуге болады (7.23-сурет).
Келлер теңдеуі бойынша өнімді экстрополяциялауды меншікті төмендеудің өнімге тәуелділігі түзу сызықпен көрсетілсе ғана жүргізуге болады
S = aQx + bQx2
Экстрополяция шегі
Sx ≤ (1,75 ч 2,0) Smax.
Альтовский теңдеуі. Өнімнің төмендеуге тәуелділігін логарифмдік функциямен көрсетеді
Q = a + b lgS.
а және в параметрлері сутарту мәліметтері бойынша ең аз дегенде екі өнім бойынша есептеледі:
a = Qi – b lgSi.
Бұл тәуелділік графикалық түрде 7.24, а суретінде көрсетілген; түзу сызықты түрге келтірілген.
Q = a + в lg Sx
палиграфиялық масштабта өнімнің төмендеуге тәуелділігі (7.24, б-суреті) түзу сызықпен көрінген жағдайда.
Экстрополяциялау шегі Sx
≤ (2,0 ч 3,0) Smax.
Смрекер теңдеуі өнім мен төмендеу арасындағы дәрежелік тәуелділікті сипаттайды
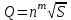, m және n сутарту мәліметтері бойынша анықталатын параметрлер.
, 
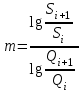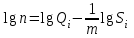. (7.65) логарифмдік өрнек келесідегідей нәтиже береді:
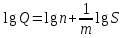. Бұл теңдеу логарифмдік масштабта, координат осьтерінде тұрғызылған түзу ретінде көрінеді
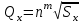
өнімнің төмендеуге тәуелділігі осьтердің логарифмдік масштабты графигінде түзу сызықпен жүргізіледі.
Экстраполяциялау шегі Sx ≤ (1,5 ч 1,75) Smax .
Эксплуатациялық қорларды өнім қисықтары бойынша есептеу үшін сутарту нәтижелерін дұрыс пайдалану үшін келесі кезектілікті сақтау керек:
1) тәжірибелік мәліметтер бойынша өнімнің төмендеуге тәуелділік графигі тұрғызылады Q = f(S); егер график координаттар басы арқылы өтетін түзу сызық ретінде болса (7.20-сурет), онда эксплуатациялық өнім (7.57) формуласы бойынша анықталады;
2) түзу сызықтан айрықша Q=f(S) графигін алу кезінде So= f(Q); lgS = f(Q); lgS = f(lgQ) функциясының графиктері тұрғызылады; осы графиктердің кез-келгенін түзу сызық ретінде алу кезінде есептеу үшін сәйкес есептік (7.60), (7.64), (7.69) формулалары қолданылады.
Пайдаланулық қорлар гидродинамикалық тәсілмен бірнеше өзара байланысатын ұңғымалардың қосындылық өнімі ретінде анықталады.
Есептеу негізіне тәжірибелік сутартудың нәтижелері және көрші ұңғымалардағы деңгейдің байқалатын срезкалар алынады. Сутартуды тек тәжірибелік ұңғымаларда ғана емес, сонымен қатар сутарту әсер ететін зонада орналасқан қазындыларда да деңгей тұрақталғанға дейін жүргізу керек.
Егер 1-ұңғымада S1 төмендеумен сутарту жүргізілсе (7.26, а-сурет), онда 1-ұңғымамен өзарабайланыстағы 2-ұңғымада деңгейдің срезкасы t21 жүреді.
Осыған ұқсас 1-ұңғымадан S1 төмендеумен сутарту кезінде 1-ұңғымада деңгейдің срезкасы t12 (7.26, б-сурет). Екі ұңғымадан бер мезгілде сутарту кезінде (7.27, а-сурет) әрбір ұңғыманың өнімі әрбір ұңғымадан жеке сутарту кезіндегі өніммен салыстырғанда төмендейді
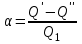, мұндағы α өнімнің төмендеу коэффициенті;
Q′ өзара байланысы жоқ ұңғыма өнімі;
Q′ = q S;
Q″ көрші ұңғымамен өзара байланыс бар кездегі сол ұңғыманың өнімі.
Өзара байланыстағы ұңғымаларды есептеу кезінде деңгейдің төмендеуін статикалық деңгейден емес, ал срезка шамасына азайғаннан есептеу керек (S - t) (7.25, б - сурет).
Бұдан q меншікті өнім арқылы көрсетілген, өзара байланыстағы ұңғымалардың өнімі тең, Q′ = g (S-t).
Q′ және Q″ шамаларын (7.70) теңдеуіне қойып, аламыз
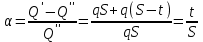. Өнімнің төмендеу коэффициенті арқылы (7.70) теңдеуінен өзара байланыстағы ұңғымалардың өнімі алынады
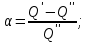
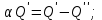
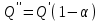
немесе
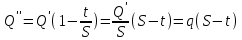. Осындай жолмен, бір ұңғыма өнімі басқа ұңғымамен өзара байланысуы кезінде екі формула бойынша анықталады:
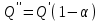немесе 
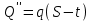. Негізгі әдебиет: (3 нег.[156-164]); Қосымша әдебиет: (4 қос.[71-78])
Бақылау сұрақтары:
-
Жерасты суларының пайдаланулық қорларын гидравликалық тәсілмен бағалаудың артықшылықтары және кемшіліктері. -
Жерасты суларының пайдаланулық қорларын бағалаудың гидравликалық тәсілі кезінде өзара әрекеттескен ұңғымалар тәсілінің маңызы неде? -
Сутарту нәтижелері өнімнің қисықтарын экстраполяциялау тәсілінің маңызы.
11 – дәріс. Жерасты суларының пайдаланулық қорларын баланстық тәсілдермен бағалау.
Мазмұны: Пайдаланулық қорларды бағалаудың баланстық тәсілі сутартқыш ғимараттарының әсер ету зоналары үшін жерасты суларының баланстық теңдеуін құрастыруға негізделген.
Баланстық теңдеуді құрастыру кезінде өнім табиғи қорлардың бір бөлігі, табиғи ресурстардың жолдан ұсталуы (перехват), қосымша қоректену көздерінен түсуі және т.б. есебінен қалыптасады деп қабылданады. Баланстық тәсіл жерасты жерасты суларын алудың жалпы пайдаланулық мүмкіндіктерін бағалау үшін қолданылады және пайдалану учаскесінде жерасты суларының деңгейінің орташа төмендеу шамасын анықтайды. Тәсілдің кемшілігі сутартқыштың деңгейді нақты ұңғымаларында анықтаудың мүмкін еместігін жатқызуғы болады.