Файл: белорусский государственный технологический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 1122
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
УДК 557.114:616-006
Студ. А.А. Дубкова, В.С. Прищепа Науч. рук. доц. Я.Г. Грода
(кафедра механики и конструирования, БГТУ)
1 ... 121 122 123 124 125 126 127 128 ... 137
КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКОГО МЕХАНИЗМА
Задача определения скоростей и ускорений точек плоского меха- низма является одной из стандартных в рамках курса теоретической ме- ханики. Следует отметить, что ее точность значительно возрастает при увеличении числа подвижных звеньев исследуемого механизма. Тем не менее, метод мгновенного центра скоростей позволяет с успехом ее ре- шить.
В качестве примера рассмотрим представленный на рис. 1, меха- низм с 5 подвижными звеньями длины которых заданы на рисунке.
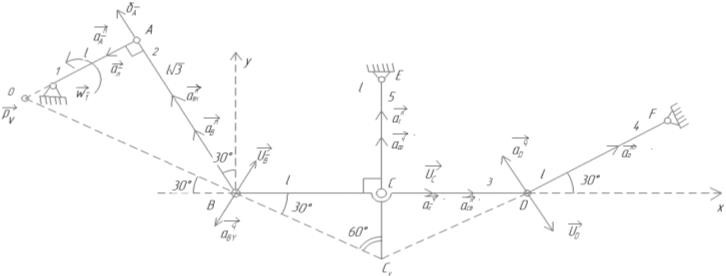
Рисунок – Вид механической системы
Решение задачи следует начать с определения по данным условия скорости и ускорения точки А рассматриваемого механизма. После чего могут быть определены направления скоростей точек D и С и по- ложения мгновенных центров скоростей звеньев АВи ВD.
На основании теоремы о проекции скоростей точек А и В на пря- мою АВможет быть найдена скорость точки В.
3
A Bcos ,
B 2A 2l .
Для определения ускорения точки В следует трижды воспользо- ваться теоремой о сложении ускорений точек плоского механизма при- нимая в качестве полюса точки А, Си D, соответственно. С учетом того, что данная теорема является векторной, проектируя каждое из получен- ных соотношений на оси Bxи By, можно получить систему 6 уравнений с шестью неизвестными величинами. При этом искомыми являются лишь две из них – проекции вектора ускорения точки ВaBна соответ- ствующие оси.
Разрешив данную систему уравнений относительно указанных проекций вектора ускорения получим
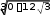 aB 2l .
aB 2l .УДК 557.114:616-006
Студ. Д.М. Климова, А.Д. Хрущ Науч. рук. ассист. Э.Э. Бильданов (кафедра механики и конструирования, БГТУ)
РАВНОВЕСИЕ СИСТЕМЫ ТРЕХ ТЕЛ
При изготовлении различного вида стержневых конструкций, шарнирно скрепленных между собой, необходимо определить абсо- лютные значения сил реакций, возникающих вследствие внешних воз- действий. В данной работе рассматривается вариант составной кон- струкции из трёх невесомых стержней. К активным силам относятся: сосредоточенная сила F, пара сил с моментом M и распределённая нагрузка на участке ВС, изменяющаяся по линейному закону, с интен- сивностью q в точке В и 2q – в С. Связи: жёсткая заделка в точке А и шарнирно-неподвижная опора в точке D(рисунок 1).
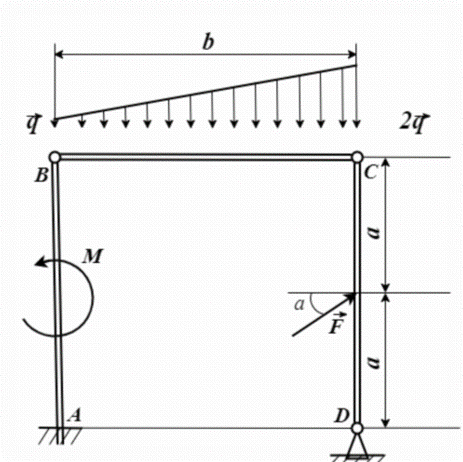 Цель данной работы: определить при каких значениях силы F: значения реакций связей в точках А и D будут одинаковыми; значение реакции связи в точке Dпримет минимальное значение.
Цель данной работы: определить при каких значениях силы F: значения реакций связей в точках А и D будут одинаковыми; значение реакции связи в точке Dпримет минимальное значение.Рисунок 1 – Шарнирно-скрепленная система трех тел
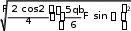 Применив условия равновесия[1, 2] для плоской произвольной системы сил были получены следующие выражения для модулей сил реакций связей в точках Аи D:
Применив условия равновесия[1, 2] для плоской произвольной системы сил были получены следующие выражения для модулей сил реакций связей в точках Аи D: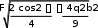 RA
RA; RD
. (1)
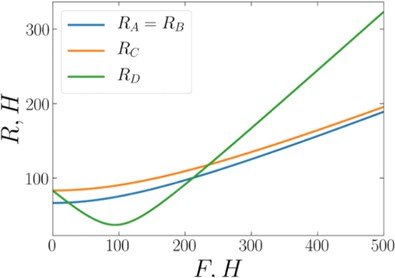
Рисунок 2 – Реакции связей в точках А, В, С, D в зависимости от силы F
при фиксированных значениях b= 2м, q = 50 Н/м, α = 45 ̊
 В системе возможны 2 случая, когда реакции в точках Аи Dравны, которые соответствуют различным направления вертикальной составляющей силы реакции в точке D.
В системе возможны 2 случая, когда реакции в точках Аи Dравны, которые соответствуют различным направления вертикальной составляющей силы реакции в точке D. F1
F1 3qb; 2sin
F2
qb ; 6sin
Rmin
5qb .
-
(2)
D
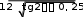 Минимум функции зависимости силы реакции в точке Dот внеш- ней силы F обусловлен наличием распределённой нагрузки q, которая действует в противоположную сторону
Минимум функции зависимости силы реакции в точке Dот внеш- ней силы F обусловлен наличием распределённой нагрузки q, которая действует в противоположную сторону ЛИТЕРАТУРА
-
Яблонский А.А. Курс теоретической механики. Ч. 1. / А.А. Яблонский, В.М. Никифорова. – М.: Интеграл-Пресс, 2007. -
В.В. Добронравов, Н. Н. Никитин. Курс теоретической меха- ники: Учебник для машиностроит. спец. вузов. – 4-е изд., перераб. и доп. / М. А. Алексеева; «Высшая школа» – Москва, 1983.
УДК 621.01
Студ. Д.В. Сакович, Т.А. Житкий Науч. рук. зав. кафедрой О.И. Карпович (кафедра механики и конструирования, БГТУ)
1 ... 122 123 124 125 126 127 128 129 ... 137
ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ ПАРАМЕТРОВ ВЯЗКОУПРУГОСТИ ТЕРМОПЛАСТИЧНЫХ ПОЛИМЕРНЫХ МАТЕРИАЛОВ В ИЗДЕЛИЯХ, ПОЛУЧЕННЫХ МЕТОДОМ 3D-ПЕЧАТИ
Одна из важных особенностей многих материалов, в частности полимерных, – зависимость напряжений и деформаций от времени, ко- торая характеризует реономные или вязкоупругие свойства. Явление уменьшения напряжений в течении времени называется релаксацией, а увеличения деформаций в течении времени ползучестью. Одна из наиболее распространенных моделей, описывающих связь между напряжениями и деформациями – модель «стандартного» вязкоупру- гого тела или тела Кельвина [1]:
р р
σ t d Eε Ht d .
dt dt
где tр – время релаксации; E– длительный модуль; H– мгновенный мо- дуль.
Параметры tр, E и H называются параметрами вязкоупругости и существенно зависят от температуры. Для моделирования поведения изделий, изготовленных из термопластичных материалов методами 3D-печати и находящихся при длительном воздействии нагрузки и по- вышенной температуры необходимы температурные зависимости па- раметров вязкоупругости. В доступной литературе для термопластич- ных материалов, которые используются в аддитивных технологиях све- дения о таких зависимостях отсутствуют.
Цель работы: исследование зависимостей параметров вязкоупру- гости образцов из ABS-пластика и PLA-пластика, полученных методом экструзии материала, от температуры