Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 271
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
«Решение нелинейных уравнений»
«Решение систем линейных алгебраических уравнений»
«Метод прогонки для трехдиагональных систем»
« Использование итерационных численных методов для решения СЛАУ»
« Использование итерационных численных методов для решения СЛАУ»
«Численное решение алгебраических проблем собственных значений»
«Интерполирование. Интерполяционные формулы»
Интерполяционная схема Эйткена
« Интерполирование. Интерполяционные формулы»
«Аппроксимация, построение аппроксимирующих кривых»
«Численное дифференцирование функции. Методы дифференцирования»
3, 8, 12, 20, 25, 36];
у = [1, 2.5, 4.6, 6.8, 5.1, 3.9, 3] ;
xi = (4, 6, 15, 30);
yi = interpl (х, у, хi) —линейная интерполяция
yi = interpl (х, у, xi, ‘linear’) — линейная интерполяция
yi = interpl (х, у, xi, ‘nearest’) —ступенчатая интерполяции
yi = interpl (х, у, xi, ‘cubic’ ) —кубическая интерполяция
yi = inrerpi (х, у, xi, ‘spline’ ) — интерполяции кубическими сплайнами.
В результате решения задачи получим следующие ответы:
Из результатов решения видно, что ответы зависят от метода интерполяции. Какой же из них предпочтительней? Ответ на этот вопрос можно дать лишь после анализа погрешностей интерполяции.
3.Система Matlab позволяет обоснованно выбрать степень полинома при полиномиальной интерполяции путем вычисления табличных разностей. Для этой цели служит функция diff. Эта функция имеет вид:
diff (v,n).
Здесь:
Полиномиальная аппроксимация имеет смысл лишь тогда, когда n-ая конечная разность функции у(х) при постоянном шаге изменения аргумента x является постоянной. При этом значение п является степенью полинома. Если это условие не выполняется, то многочлен степени п либо не может быть функцией интерполяции, либо является основным источником погрешностей.
Пусть данные эксперимента сведены в таблицу:
Необходимо решить задачу полиномиальной аппроксимации.
Вначале определим степень полинома, воспользовавшись функцией diff. Эти процедуры в системе Matlab будут иметь вид:
х = [12 3 4 5 6 7 8 9 10);
у = [18, 52.2, 121.4, 239.4, 420, 677, 1024.2, 1475.4, 2044.4, 2745];
diff(y, 1)
ans = 34.2 69.2 118 180.6 257 347.2 451.2 569 700.6
diff(у, 2)
ans =35 48.8 62.6 76.4 90.2 104 117.8 131.6
diff(y, 3)
ans = 13.8 13.8 13.8 13.8 13.8 13.8 13.8
Табличные разности третьего порядка одинаковы, поэтому интерполяционный полином будет иметь вид:
φ(x) = ах3+ bx2 + сх + d.
Определим теперь значения коэффициентов а, d, с, d воспользовавшись функцией polyfit.
Так как векторы аргумента х и функции у уже введены, то достаточно ввести функцию polyfit.
р = polyfit(х, у, 3)
р = 2.3 3.7 7 5
Подставляя полученные значения в функцию у(х), получим:
φ(x) = 2.3 х3+ 3.7 x2 +
7х + 5.
Проверим правильность решения задачи, воспользовавшись функцией polyval:
f = polyval(p, х)
f = 18 52.2 121.4 239.4 420 677 1024.2 1475.4 2044.4 2745
Сравнивая значения fс исходными значениями у, видим, что они совпадают. Задача решена с нулевой погрешностью.
Содержание отчета:
Контрольные вопросы:
Цель: научиться подбирать аппроксимирующий полином первой и второй степени и строить соответствующие аппроксимирующие кривые.
Задание:
Варианты заданий:
Теоретический материал:
Аппроксимация функций с помощью метода наименьших квадратов
Метод наименьших квадратов применяется при обработке результатов эксперимента для аппроксимации (приближения) экспериментальных данных аналитической формулой. Конкретный вид формулы выбирается, как правило, из физических соображений. Такими формулами могут быть:
и другие.
Пример решения в MatLab:
>> x=[1 2.2 2.4 2.7 3.1 3.5 4.5 5];
>> y=[9.054 15.077 15.754 18.3 17.984 15.852 1.772 -13.042];
>> a=polyfit(x,y,1)
a =
-5.4276 26.6479
>> x1=0.9:0.5:5.1;
>> y1=polyval(a,x1);
>> plot(x1,y1,'-k',x,y,'ok')
>> a=polyfit(x,y,2)
a =
-4.7042 23.6773 -11.5522
>> x1=0.9:0.5:5.1;
>> y1=polyval(a,x1);
>> plot(x1,y1,'-k',x,y,'ok')
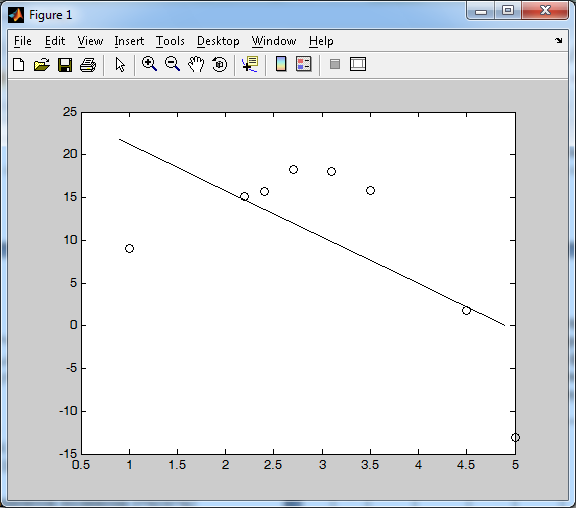
Рисунок 5. График функции
>> a=polyfit(x,y,3)
a =
-1.3534 7.2257 -6.9270 10.0393
>> x1=0.9:0.5:5.1;
>> y1=polyval(a,x1);
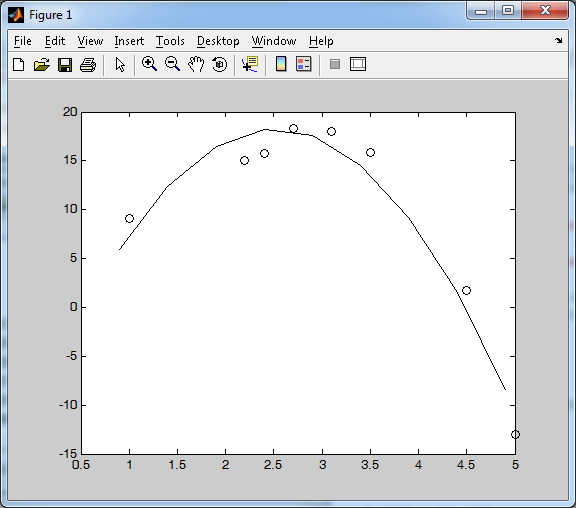
Рисунок 6. График функции
у = [1, 2.5, 4.6, 6.8, 5.1, 3.9, 3] ;
xi = (4, 6, 15, 30);
yi = interpl (х, у, хi) —линейная интерполяция
yi = interpl (х, у, xi, ‘linear’) — линейная интерполяция
yi = interpl (х, у, xi, ‘nearest’) —ступенчатая интерполяции
yi = interpl (х, у, xi, ‘cubic’ ) —кубическая интерполяция
yi = inrerpi (х, у, xi, ‘spline’ ) — интерполяции кубическими сплайнами.
В результате решения задачи получим следующие ответы:
-
линейная интерполяция: 2.92 3.76 6.1625 3.4909; -
ступенчатая интерполяция: 2.5 4.6 6.8 3.9; -
кубическая и кубическая сплайнами: 3.4133 4.16 6.9772 3.5263.
Из результатов решения видно, что ответы зависят от метода интерполяции. Какой же из них предпочтительней? Ответ на этот вопрос можно дать лишь после анализа погрешностей интерполяции.
3.Система Matlab позволяет обоснованно выбрать степень полинома при полиномиальной интерполяции путем вычисления табличных разностей. Для этой цели служит функция diff. Эта функция имеет вид:
diff (v,n).
Здесь:
-
v — вектор функции y(x); -
п — порядок конечных разностей.
Полиномиальная аппроксимация имеет смысл лишь тогда, когда n-ая конечная разность функции у(х) при постоянном шаге изменения аргумента x является постоянной. При этом значение п является степенью полинома. Если это условие не выполняется, то многочлен степени п либо не может быть функцией интерполяции, либо является основным источником погрешностей.
Пусть данные эксперимента сведены в таблицу:
| | Значения переменных | |||||||||
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 18 | 52.2 | 121.4 | 239.4 | 420 | 677 | 1024.2 | 1475.4 | 2044.4 | 2745 |
Необходимо решить задачу полиномиальной аппроксимации.
Вначале определим степень полинома, воспользовавшись функцией diff. Эти процедуры в системе Matlab будут иметь вид:
х = [12 3 4 5 6 7 8 9 10);
у = [18, 52.2, 121.4, 239.4, 420, 677, 1024.2, 1475.4, 2044.4, 2745];
diff(y, 1)
ans = 34.2 69.2 118 180.6 257 347.2 451.2 569 700.6
diff(у, 2)
ans =35 48.8 62.6 76.4 90.2 104 117.8 131.6
diff(y, 3)
ans = 13.8 13.8 13.8 13.8 13.8 13.8 13.8
Табличные разности третьего порядка одинаковы, поэтому интерполяционный полином будет иметь вид:
φ(x) = ах3+ bx2 + сх + d.
Определим теперь значения коэффициентов а, d, с, d воспользовавшись функцией polyfit.
Так как векторы аргумента х и функции у уже введены, то достаточно ввести функцию polyfit.
р = polyfit(х, у, 3)
р = 2.3 3.7 7 5
Подставляя полученные значения в функцию у(х), получим:
φ(x) = 2.3 х3+ 3.7 x2 +
7х + 5.
Проверим правильность решения задачи, воспользовавшись функцией polyval:
f = polyval(p, х)
f = 18 52.2 121.4 239.4 420 677 1024.2 1475.4 2044.4 2745
Сравнивая значения fс исходными значениями у, видим, что они совпадают. Задача решена с нулевой погрешностью.
Содержание отчета:
-
Титульный лист. -
Цель лабораторной работы. -
Исходные данные, указываемые в задании и необходимые для достижения поставленной цели. -
Расчетная часть: описание выполнения задания -
Проверка результатов в среде MatLab. -
Выводы и анализ полученных результатов.
Контрольные вопросы:
-
Интерполяционный многочлен Ньютона; -
В каких случаях ставится задача интерполирования функций? -
Какой формулой Вы пользовались для интерполирования? -
Какие узлы интерполирования даны в Вашем случае (равноотстоящие или произвольные)? -
Какие интерполяционные формулы используются при произвольных узлах? -
В чем заключается кусочная интерполяция? -
Какие функции используются для интерполирования функции в среде MatLab? -
Что находит функция p = polyfit(x, y, n);
Лабораторная работа №12.
«Аппроксимация, построение аппроксимирующих кривых»
Цель: научиться подбирать аппроксимирующий полином первой и второй степени и строить соответствующие аппроксимирующие кривые.
Задание:
-
Подобрать аппроксимирующий полином первой и второй степени, используя метод наименьших квадратов. -
Используя среду MatLab подобрать аппроксимирующий полином первой, второй и третьей (если необходимо, то четвертой и т.д.) степени и построить соответствующие аппроксимирующие кривые. -
Найти значение функции в точке х.
Варианты заданий:
| Вариант | xi | 1 | 2 | 3 | 4 | 5 | [a;b] | x |
| 1 | yi | 0,7 | 1,9 | 1,1 | 2,2 | 3,5 | [2;2.5] | 2.2 |
| 2 | yi | 0,8 | 2,4 | 1,5 | 2,3 | 4,0 | [5;5.8] | 5.4 |
| | | | | | | | | |
| 3 | yi | 2,1 | 3,0 | 1,5 | 3,2 | 4,1 | [2;2.9] | 2.3 |
| 4 | yi | 2,2 | 4,8 | 1,9 | 3,9 | 5,5 | [1;2,2] | 1.9 |
| 5 | yi | 1,0 | 3,5 | 5,0 | 5,6 | 3,8 | [3;4.1] | 3.8 |
| 6 | yi | 2,6 | 1,1 | 1,6 | 3,2 | 2,4 | [4;4.3] | 4.1 |
| 7 | yi | 3,5 | 4,8 | 3,5 | 1,8 | 1,5 | [2;2.6] | 2.3 |
| 8 | yi | 6,0 | 3,2 | 1,9 | 1,3 | 1,2 | [1;1,9] | 1.2 |
| 9 | yi | 1,5 | 1,8 | 2,5 | 4,0 | 7,0 | [1;1,4] | 1.1 |
| 10 | yi | 0 | 6,0 | 2,0 | 1,3 | 6,0 | [3;3,9] | 3.5 |
| 11 | yi | 3,5 | 1,2 | 0 | 1,7 | 2,0 | [6;6,3] | 6.7 |
| 12 | yi | 1,4 | 2,7 | 6,0 | 0 | 4,8 | [4;4,7] | 4.6 |
| 13 | yi | 2,1 | 3,1 | 5,1 | 5,8 | 6,0 | [4;4,5] | 4,1 |
| 14 | yi | 1,0 | 3,5 | 5,0 | 5,6 | 3,8 | [3;4.1] | 3.6 |
| 15 | yi | 2,6 | 1,1 | 1,6 | 3,2 | 2,4 | [4;4.3] | 4.2 |
Теоретический материал:
Аппроксимация функций с помощью метода наименьших квадратов
Метод наименьших квадратов применяется при обработке результатов эксперимента для аппроксимации (приближения) экспериментальных данных аналитической формулой. Конкретный вид формулы выбирается, как правило, из физических соображений. Такими формулами могут быть:
-
Y=ax+b, -
Y=ax2+bx+c, -
Y=anxn+an-1xn-1+….+a1x+a0 -
Y=aedx+c, y=a/x+b
и другие.
Пример решения в MatLab:
-
Введем исходные данные
>> x=[1 2.2 2.4 2.7 3.1 3.5 4.5 5];
>> y=[9.054 15.077 15.754 18.3 17.984 15.852 1.772 -13.042];
-
Вычислим вектор коэффициентов полинома Y=ax+b
>> a=polyfit(x,y,1)
a =
-5.4276 26.6479
-
Вычислим значения полинома на интервале от 10 до 20
>> x1=0.9:0.5:5.1;
>> y1=polyval(a,x1);
-
Построим график полинома и экспериментальных точек в одной графической области
>> plot(x1,y1,'-k',x,y,'ok')
-
По графику определяем что данная кривая неподходит (см. Рисунок 5). -
Поэтому далее вычисляем вектор коэффициентов полинома Y=ax2+bx+c
>> a=polyfit(x,y,2)
a =
-4.7042 23.6773 -11.5522
-
Вычислим значения полинома на интервале от 10 до 20
>> x1=0.9:0.5:5.1;
>> y1=polyval(a,x1);
-
Построим график полинома и экспериментальных точек в одной графической области
>> plot(x1,y1,'-k',x,y,'ok')

Рисунок 5. График функции
-
Имеем график (см. Рисунок 6) -
Найдем еще вектор коэффициентов полинома Y=ax3+bx2+cх+d
>> a=polyfit(x,y,3)
a =
-1.3534 7.2257 -6.9270 10.0393
-
Вычислим значения полинома на интервале от 10 до 20
>> x1=0.9:0.5:5.1;
>> y1=polyval(a,x1);

Рисунок 6. График функции
-
Построим график полинома и экспериментальных точек в одной графической области