Файл: Организация медикосоциальных исследований и методы статистического анализа Модуль Абсолютные и относительные статистические показатели Цель изучения модуля.doc

), все элементы которой упорядочены по возрастанию, называется вариационным рядом. Элемент вариационного ряда – варианта. Каждое из значений в выборке может встречаться неоднократно, количество одинаковых вариант для каждого называется его частотой . Если число различных значений в выборке обозначить , где , то .

Соответственно величина называется относительной частотой для значения . Обязательно, . Множество выборочных значений и соответствующих им относительных частот называется выборочным (статистическим) распределением:

			…
			…

Средняя арифметическая простая – средняя вариационного ряда

---

, где каждая варианта записана столько раз, сколько встречается. Вычисляется по формуле

.

Среднюю арифметическую значений можно записать иначе, с учетом частоты повторений каждого из значений. Получаем среднюю арифметическую взвешенную вариационного ряда, где k различных значений, k≤n.

---

Тогда средняя арифметическая взвешенная записывается как

,

где каждое число - частота соответствующего значения , причем

.
Формулу расчета средней арифметической взвешенной можно представить в следующем виде:



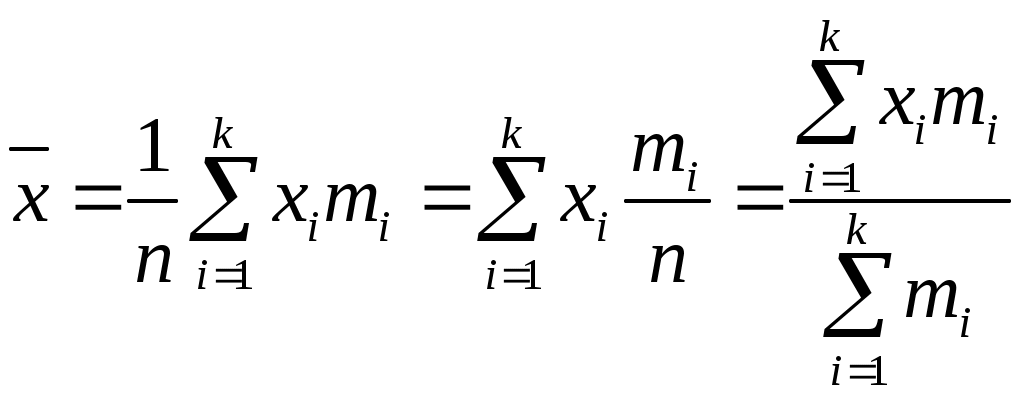
Средняя арифметическая простая и средняя арифметическая взвешенная это одна и та же величина. Различие лишь в записи расчетной формулы.

Средняя арифметическая является математическим ожиданием выборки из изучаемой генеральной совокупности и среди оценок математического ожидания генеральной совокупности является наиболее распространенной.
3.2. Задания для самостоятельной работы

1. 
   Изучить материалы соответствующей главы учебника, модуля, рекомендуемой литературы.
   
2. 
   Ответить на контрольные вопросы.
   
3. 
   Разобрать задачу-эталон.
   
4. 
   Ответить на вопросы тестового задания модуля.
   
5. 
   Решить задачи для самостоятельного решения.
   

3.3. Контрольные вопросы

1. 
   Дайте определение средней величины, вариационного ряда, выборочного распределения.
   
2. 
   Назовите условия, которые необходимо соблюдать при расчете средних величин.
   
3. 
   Перечислите виды средних величин, используемые в медико-социальных исследованиях? Приведите примеры их применения.
   

4. Дайте определение терминам «мода» и «медиана».

5. Назовите виды средней арифметической. Приведите способы их расчета.
3.4. Задача-эталон

Исходные данные

1. При измерении роста детей в старшей группе детского сада получены следующие значения: 115, 116, 118, 119, 121,122,123, 124,125, 126; 127, 128, 129 см.

2. При изучении длительности лечения в стационаре больных пневмонией получены следующие значения

---

, представленные в таблице 3.1.
Таблица 3.1. Длительность лечения в стационаре больных пневмонией (дни)

Длительность лечения, xi	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
Частота, mi	2	2	3	5	5	7	9	12	8	6	3	3	2	1	1

Задание

1. На основании представленных исходных данных рассчитать средний рост детей в старшей группе детского сада.

2. На основе представленных исходных данных рассчитать среднюю длительность лечения в стационаре больных пневмонией.
Решение

1. Рассчитываем среднюю арифметическую роста простую:



Вывод_Средний_рост_детей_в_данной_группе_составил_122,5_см.2.'>Вывод

Средний рост детей в данной группе составил 122,5 см.
2. Рассчитываем среднюю арифметическую взвешенную для показателя длительности лечения:




Вывод

Средняя длительность лечения в стационаре больных пневмонией - 17,5 дня.
3.5. Тестовые задания

Выберите только один правильный ответ.
1. дайте определение средней величины:

1. Число, выражающее общую меру количественного признака в совокупности.

2. Величина, отражающая общее свойство статистической совокупности.

3. Величина, представляющая собой обобщенную количественную характеристику статистической совокупности.

4. Величина, показывающая размер признаков в расчете на единицу однородной совокупности.

---

5. Величина, дающая серединную характеристику признака.
2. дайте определение вариационного ряда:

1. Ряд наблюдений (выборка), все элементы которого упорядочены по возрастанию.

2. Два ряда величин, изменяющихся в убывающем или возрастающем порядке.

3. Ряд числовых значений какого-то определенного количественного порядка.

4. Статистический ряд, характеризующийся распределением чисел в убывающем или возрастающем порядке.

5. Ряд чисел, характеризующий определенный признак.
3. Дайте определение средней арифметической простой:

1. Средняя, которая определяет количество вариант в вариационном ряду.

2. Средняя, которая характеризует распределение вариант в вариационном ряду.

3. Средняя, которая получается как частное от деления суммы вариант на сумму частот.

4. Средняя вариационного ряда, вычисляемая по формуле:



5. Средняя вариационного ряда, вычисляемая по формуле:

4. Какая из перечисленных величин не относится к средним величинам?

1. Мода.

2. Медиана.

3. Средняя арифметическая.

4. Средняя простая.

5. Средняя геометрическая.
5. ВАРИАНТОЙ НАЗЫВАЮТ

1. Любое числовое значение нескольких признаков.

2. Элемент характеристики изучаемых признаков.

3. Элемент вариационного ряда.

4. Частоту вариационного ряда.

5. Числовое значение абсолютных величин.
6. Дайте определение средней арифметической взвешенной

1. Средняя, которая определяет количество вариант в вариационном ряду.

2. Средняя, которая характеризует распределение вариант в вариационном ряду.

3. Средняя, которая получается как частное от деления суммы вариант на сумму частот.

4. Средняя вариационного ряда, вычисляемая по формуле:



5. Средняя вариационного ряда, вычисляемая по формуле:

7. СРЕДНИЕ ВЕЛИЧИНЫ ИСПОЛЬЗУЮТСЯ ДЛЯ:

1. Анализа показателей частоты распространения явлений в своей среде.

2. Получения обобщенной характеристики изучаемого признака.

3. Определения уровней здоровья населения.

4. Изучения структуры изучаемых совокупностей.

5. Изучения структуры изучаемых явлений.
8. КАКАЯ ХАРАКТЕРИСТИКА ОБЩЕСТВЕННОГО ЗДОРОВЬЯ ВЫРАЖАЕТСЯ СРЕДНИМИ ВЕЛИЧИНАМИ?

---