Файл: Учебнометодический комплекс для проведения практических занятий по дисциплине Управление проектами.docx

в) структуры временных интервалов и организационной структу-

ры;

г) структуры ресурсов и функциональной структуры.

8. 
   Описание и согласования структуры ответственности за выпол-нение наборов работ обеспечивает:
   

а) структура разбивки работ; в) матрица ответственности;

б) матрица приоритетов; г) организационная структура.

9. 
   Назначение ответственных за выполнение работ проекта происходит на этапе:
   

а) планирования; в) контроля;

б) выполнения; г) завершения.

10. 
    К параметрам, по которым осуществляется структуризация проекта, не относятся:
    

а) этапы жизненного цикла проекта;

б) компоненты продукта;+

в) виды участия в выполнении работ;

г) подразделения организационной структуры;

д) элементы затрат.

2.6 Сетевое и календарное планирование проекта.

План семинарского занятия

1. 
   Сущностная характеристика и значение сетевого и календар-ного планирования.
   
2. 
   Теоретико - методические основы разработки сетевого графика.
   
3. 
   Расчет параметров сетевого графика.
   
4. 
   Диаграмма Ганта как инструмент календарного планирова-ния.
   

2.6.1 Сущность и основные элементы сетевого планирования и управления

Чем сложнее планируемая работа или проект, тем сложнее задачи оперативного планирования, контроля и управления. В этих условиях применение календарного графика не всегда может быть достаточно удовлетворительным, особенно для большого и сложного объекта, поскольку не позволяет обоснованно и оперативно планировать, выбирать оптимальный вариант продолжительности выполнения работ, использовать резервы и корректировать график в ходе деятельности. Перечисленные недостатки линейного календарного графика в значительной мере устраняются при использовании системы сетевых моделей, которые позволяют анализировать график, выявлять резервы и использовать электронно-вычислительную технику. Применение сетевых моделей обеспечивает продуманную детальную организацию работ, создает условия для эффективного руководства.

Весь процесс находит отражение в графической модели, которую называют сетевым графиком. В сетевом графике учитываются все работы от проектирования до ввода в действие, определяются наиболее важные, критические работы, от выполнения которых зависит срок окончания проекта. В процессе деятельности имеется возможность корректировать план, вносить изменения, обеспечивать непрерывность в оперативном планировании. Существующие методы анализа сетевого графика позволяют оценивать степень влияния внесенных изменений на ход осуществления программы, прогнозировать состояние работ на будущее. Сетевой график точно указывает на работы, от которых зависит срок выполнения программы.

---

Сетевое планирование и управление (СПУ) - это совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ с помощью сетевого графика (сетевой модели).

Под комплексом работ мы будем понимать какую - либо задачу, для выполнения которой необходимо осуществить большое количество разнообразных работ. Для того чтобы составить план работ по выполнению больших и сложных проектов, включающих тысячи отдельных исследований и операций, необходимо описать их с помощью математической модели. Таким средством описания проектов является сетевая модель.

Сетевая модель - это план выполнения определенного комплекса взаимозависимых работ, заданных в форме сетки, графическое изображение которой называется сетевым графиком.

Главными элементами сетевой модели являются работы и события. Термин работа в СПУ имеет несколько значений. Во - первых, это настоящая работа - процесс, который длится во времени и требует затрат ресурсов (например, изготовление изделия, испытания прибора и т.п.). Каждая работа должна быть конкретной, четко описанной и иметь ответственного исполнителя.

Во - вторых, это ожидание, которое длится во времени - процесс, не требующий затрат труда (например, процесс сушки после покраски, застывание бетона и т.п.).

В - третьих, это зависимость, или фиктивная работа - логическая связь между двумя или несколькими работами (событиями), не требующие затрат труда, материальных ресурсов или времени. Она показывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.

Событие - это момент завершения определенного процесса, отражающий отдельный этап выполнения проекта. Событием может быть частичный результат отдельной работы или суммарный результат нескольких работ. Событие может осуществиться только тогда, когда закончатся все работы, которые ему предшествуют. Последующие работы могут начаться только тогда, когда событие осуществилось.

Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечной, а для всех непосредственно следующих за ним - начальной. При этом предполагается, что событие не имеет продолжительности и осуществляется как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

---

При составлении сетевых графиков (моделей) используют условные обозначения. События на сетевом графике (или, как еще говорят, на графе) изображаются кружками (вершинами графа), а работы - стрелками (рисунок 2.3)



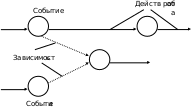
Рисунок 2.3 - Основные элементы сетевой модели

Зависимость (фиктивная работа) - применяется для упрощения сетевых графиков (продолжительность всегда равна 0).

Среди событий сетевой модели выделяют исходные и завершающие события.

Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ.

Завершающее событие не имеет последующих работ и событий.

Критический путь - путь в сеточной модели, длительность которого равна критической.

Критическая продолжительность - минимальная продолжительность, в течение которого может быть выполнен весь комплекс работ проекта.

Расчет параметров сетевого графика содержит определенный перечень временных показателей.

Основными параметрами сетевого графика являются:

а) Tpi - раннее время осуществления i - го события.

Это время, необходимо для выполнения всех предыдущих работ данного события.

H

T_pi = L⋅( )max, (2.12)

i

где L - путь;

H - начальное (исходное) событие всей разработки; i - событие.

б) tпi - позднее время осуществления i - го события. Это такое время наступления события, превышение которого вызывает аналоги- чную задержку наступления завершающего события:

і

T_пi = L_кр − L⋅( )max, (2.13)

К

где L_кр - длина критического пути;

К - завершающее (конечное) событие всей разработки;

в) Ri - резерв времени события. Это такой промежуток времени, на который может быть отсрочено наступление i - го события без нарушения сроков завершения разработки в целом:

R_i = T_пі −Т _рі (2.14)

г) Rпij - полный резерв работы ij. Это максимальное количество

времени, на которое можно увеличить продолжительность данной работы, не меняя продолжительность критического пути:

R_пij = T_пj −Т _рі −t_ij (2.15) где tij - продолжительность выполнения работы ij.

д) Rcij - свободный резерв работы ij. Это максимальное количество времени, на которое можно увеличить продолжительность данной работы, не изменяя при этом ранних сроков начала следующих работ:

R_cIj = T

---

_pj −Т _рі −t_ij (2.16)

е) K_нij - коэффициент напряженности работы ij. Он показывает степень трудности выполнения работы, в установленный срок:

t_ij

^К_Н = (2.17)

t ij +Rnij

После расчета перечисленных параметров можно определить:

Т_pнij - ранний срок начала работы ij;

Т_pнij = Т_pi; (2.18)

Т_пнij - поздний срок начала работы ij;

Т_пнij = Т_пj – t_ij; (2.19)

Т_poij – ранний срок окончания работы ij;

Т_poij = Т_pi + t_ij; (2.20)

Т_пoij– поздний срок окончания работы ij;

Т_пoij = Т_пj. (2.21)

Рассмотрим способ расчета параметров сетевого графика без посредственно на сети (рисунок 3.2).



Рис 2.4 - Пример расчета параметров непосредственно на сети

Каждое событие делится на четыре сектора, в верхнем секторе указывается номер события, в левом - раннее время совершения события, в правом - позднее время совершения событий, в нижнем секторе - резерв события. Над стрелкой (работой) указывается время, необходимое для выполнения данной работы.

Параметры сети рассчитываются следующим образом.

При движении слева направо заполняются только левые сектора, причем за раннее время совершения события принимается наибольшее значение суммарного времени из всех путей, ведущих к данному событию.

Определение позднего времени совершения событий ведется строго в обратном направлении - от заключительного до исходного события. Исходя из того, что какая - либо разработка должна быть закончена в кратчайшее время, позднее время осуществления завершающего события принимается равным раннему сроку его осуществления и этот показатель записывается в правый сектор.

После этого начинают рассчитывать поздние сроки наступления всех других событий, справа налево. В правые сектора всех событий записывают минимальное значение разности между поздним временем наступления одного из следующих событий и продолжительностью работы, соединяющей это событие с предыдущим.

Чтобы определить резерв времени события, нужно из числового значения правого сектора отнять числовое значение левого сектора данного события.

Чтобы определить полный резерв работы, нужно из числового значения правого сектора следующего события данной работы отнять числовое значение левого сектора предыдущей события данной работы и продолжительность самой работы.

---

Чтобы определить свободный резерв работы, нужно из числового значения левого сектора следующего события данной работы отнять числовое значение левого сектора предыдущего события данной работы и продолжительность самой работы.

Чтобы определить коэффициент напряженности работы, следует разделить продолжительность работы на продолжительность этой же работы плюс полный резерв работы.

Чтобы выделить критический путь, следует определить последовательность взаимосвязанных работ, имеющих нулевые резервы времени, и коэффициенты напряженности, равны единице. Критический путь на графике выделяется жирной или двойной линией.

Пример расчета сетевого графика представлен на рисунке 2.5.



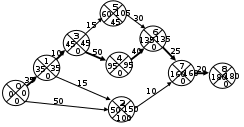
Рисунок 2.5 - Пример расчета сетевого графика

Пример расчета параметров сетевого графика приведен в таблице

2.10.

Таблица 2.10 - Расчет параметров сетевого графика

Ранний срок начала работы [левый сектор предыдущего события]	Ранний срок окончания работы [левый сектор предыдущего события плюс время работы]	Поздний срок начала работы [правый сектор следующего события минус время работы]	Поздний срок окончания работы [правый сектор следующего события]
tрн01=0	tро01=0+35=35	tпн01=35 – 35=0	tпо01=35
tрн02=0	tро02=0+50=50	tпн02=150 – 50=100	tпо02=150
tрн12=35	tро12=35+15=50	tпн12=150 – 15=135	tпо12=150
tрн13=35	tро13=35+10=45	tпн13=45 – 10=35	tпо13=45
tрн27=50	tро27=50+10=60	tпн27=160 – 10=150	tпо27=160
tрн34=45	tро34=45+50=95	tпн34=95 – 50=40	tпо34=95
tрн35=45	tро35=45+15=60	tпн35=105 – 15=90	tпо35=105
tрн46=95	tро46=95+40=135	tрн46=135 – 40=95	tпо46=135
tрн56=60	tро56=60+30=90	tпн56=135 – 30=105	tпо56=135
tрн67=135	tро67=135+25=160	tпн67=160 – 25=135	tпо67=160
tрн78=160	tро78=160+20=180	tпн78=180 – 20=160	tпо78=180

---