МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ

АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет «Дорожно-транспортный»

Кафедра «Математическое моделирование»

ТИПОВОЙ РАСЧЕТ

по дисциплине

«Теория вероятностей и математическая статика»
Выполнил:
студент II курса
группы АС-21
Москалёв И.В.
№ зачетной книжки 21-006
Проверил:
Заведующий кафедрой, профессор. д.т.н. Вовк Л.П.

Горловка 2023

№1

Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?

Решение

Различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно составить 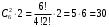шт. (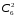 способами выбираем два числа из 6, и двумя способами составляем из них дробь: сначала одно число – числитель, другое знаменатель и наоборот).

Из этих 30 дробей ровно 15 будут правильные (т.е., когда числитель меньше знаменателя): 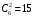способами выбираем два числа из 6, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя.

Ответ: 30; 15.

№2

Сколько существует шестизначных чисел, все цифры которых имеют одинаковую чётность?

Решение

Из нечетных цифр 5⁶ т. к. 0 не может быть первым.

Из чётных цифр:

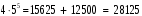
Ответ: 28125.

№3

Сколько пар натуральных чисел удовлетворяет равенству ?

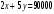Решение



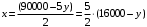
16000 – у кратно 2 и не равно 0, иначе х = 0, а 0 – не натуральное число. Поэтому у кратно 2 и принадлежит промежутку (0;16000).

Найдём сколько чисел кратных 2 входит в этот промежуток:



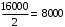
Ответ: 8000.

№4

Каждую клетку квадратной таблицы 2×2 можно покрасить в чёрный или белый цвет. Сколько существует различных раскрасок этой таблицы?

---

Решение

В каждой из 2х2 = 4 клеток может быть 2 варианта раскраски. То есть, есть 2 варианта раскраски первой клетки, на каждый из них есть по 2 подварианта раскраски второй клетки, на каждый из них по 2 подварианта для третьей и так же для четвёртой клетки.

Получим: 2·2·2·2 = 16 вариантов.

Ответ: 16.

№5

Слово – любая конечная последовательность букв русского алфавита. Выясните, сколько различных слов можно составить из слов

а) ВЕКТОР;

б) ЛИНИЯ;

в) ПАРАБОЛА;

г) БИССЕКТРИСА;

д) МАТЕМАТИКА.

Решение

а) Так как все буквы слова различны, то всего можно получить: 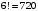слов;

б) В этом слове две буквы И, а все остальные буквы разные. Временно будем считать разными и буквы И, обозначив их через И₁ и И₂. При этом предположении получится 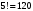разных слов. Те слова, которые получаются друг из друга перестановкой букв И₁ и И₂, на самом деле одинаковы. Таким образом, полученные 120 слов разбиваются на пары одинаковых. Поэтому разных слов всего: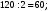

в) В этом слове 8 букв, три из которых А. Временно будем считать разными и буквы А, обозначив их через А₁, А₂ и А₃. При этом предположении получится 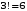разных слов. Те слова, которые получаются друг из друга перестановкой букв А₁, А₂ и А₃, на самом деле одинаковы. Таким образом, полученные 3 слова разбиваются на 8 одинаковых. Поэтому разных слов всего: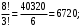

г) В этом слове три буквы С и две буквы И. Считая все буквы различными, получаем 11! слов. Отождествим слова, отличающиеся лишь перестановкой букв И, но не С: 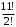слов. Теперь отождествим слова, отличающиеся перестановкой букв С: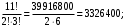

---

д) В этом слове три буквы А, две буквы Т и две буквы М. Считая все буквы различными, получаем 10! слов. Отождествим слова, отличающиеся лишь перестановкой букв Т и М, но не С: 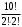слов. Теперь отождествим слова, отличающиеся перестановкой букв С: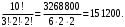

Ответ: а) 720; б) 60; в) 6720; г) 3326400; д) 151200.

№6

Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево (например, таких как 54345, 17071)?

Решение

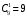способами можно выбрать цифру для разряда единиц и разряда десятков тысяч (ноль будет исключением, так как, если он находится в разряде десятков тысяч, то число не является пятизначным);

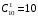способами можно выбрать цифру для разряда десятков и тысяч;

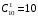способами можно выбрать цифру для разряда сотен.

Таким образом, существует 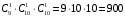пятизначных чисел, которые одинаково читаются слева направо и справа налево.

Ответ: 900.

№7

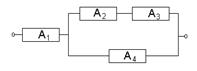Имеется электрическая цепь. Опишите, что: а) цепь будет работать, б) имеется разрыв цепи.

Решение

Ответ: .

№8

В классе 16 учеников. Каждый месяц учитель делит класс на две группы.
Какое наименьшее количество месяцев должно пройти, чтобы каждые два ученика в какой-то из месяцев оказались в разных группах?

Решение

Составим таблицу и разобьём класс на две группы так, чтобы любые два ученика в какой-то из четырех месяцев оказались в разных группах.

В ней будут преобладать следующие значения: 0 – ученик входит в первую группу; 1 – ученик входит во вторую группу.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
2	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
3	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
4	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

---

Так как в столбце можно расставить нули и единицы восемью различными способами, то в таблице найдутся два одинаковых столбца. Ученики, которым соответствуют эти столбцы, будут попадать в одну и ту же группу.



Ответ: 4 месяца.

№9

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.

Решение

Обозначим «+» такую сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону – «–», отвечающая за проигрыш. Всего возможно восемь комбинаций выпадения жребия:

1. 
   – – – 6. + – +
   
2. 
   – – + 7. + + –
   
3. 
   – + – 8. + + +
   
4. 
   – + +
   
5. 
   + – –
   

Вариант «+» для Физика только два раза возможен в трёх случаях:

+ + – + – + – + +

m = 3 – кол-во вариантов для Физика;

n = 8 – общее кол-во вариантов.



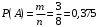
Ответ: 0,375.

№10

Найти вероятность того, что при бросании двух игральных костей выпадет от 7 до 10 очков.

Решение

Общее число исходов (возможных комбинаций цифр на двух игральных костях):

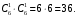
Подсчитаем количество благоприятствующих исходов:

7 очков: (1,6), (6,1), (2,5), (5,2), (3,4), (4,3);

8 очков: (2,6), (6,2), (3,5), (5,3), (4,4);

9 очков: (3,6), (6,3), (4,5), (5,4);

10 очков: (4,6), (6,4), (5,5)

Всего: 18 благоприятствующих исходов.

По классическому определению: 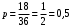– искомая вероятность.

Ответ: 0,5.

№11

Петя предлагает Васе сыграть в следующую игру. Петя дает Васе две коробки с конфетами. В каждой из двух коробок шоколадные конфеты и карамельки. Всего в обеих коробках 25 конфет. Петя предлагает Васе взять из каждой коробки по конфете. Если обе конфеты окажутся шоколадными, то Вася выиграл. В противном случае выиграл Петя. Вероятность того, что Васе достанутся две карамельки, равна 0,54. У кого больше шансов на победу?

Решение

Поскольку Вася вынет две карамельки с вероятностью 0,54, то вероятность того, что он вынет две шоколадные конфеты:

1 – 0,54 = 0,46

Т.к. вероятность выигрыша для Васи меньше 0,5 (0,5 > 0,46), то больше шансов на победу у Пети.

---

Ответ: больше шансов на победу у Пети.

№12

На окружности радиуса R=2 наугад взято две точки. Какова вероятность того, что расстояние между ними не превышает π/6, если это расстояние отсчитывается на окружности как наименьшая из дуг, их соединяющая?

Решение

Ответ: .

№13

На бесконечную шахматную доску со стороной квадрата а наудачу бросается монета радиуса 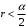. Найти вероятности следующих событий: А = «монета попадет целиком внутрь одного квадрата», В = «монета пересечет не более одной стороны квадрата».

Решение

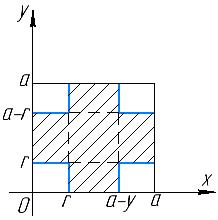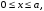
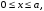
П усть (х, у) – координаты центра упавшей монеты. В силу бесконечности шахматной доски можно считать, что элементарные исходы данного эксперимента полностью определяются положением центра упавшей монеты относительно вершин квадрата, содержащего этот центр. Помещая начало координат в одну из вершин указанного квадрата, можно записать множество элементарных исходов в виде 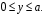Множество, соответствующее событию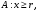 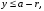т.е. является квадратом со стороной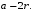

Следовательно





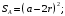
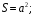
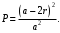
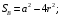
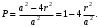
Ответ:


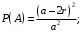
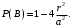
№14

Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

---

Смотрите также файлы

• Кн тртібі таырыбына трбие шараны жоспары. Трбие саатыны таырыбы.docx

• Фамилия Проверка читательских умений работать с текстом художественного произведения Прозрение.docx

• Lesson Study ді проблемалы сраы.docx

• Кіріспе зерттеуді зектілігі. Бгінде Елбасы Н.. Назарбаев ала ойан, дамыан отыз елді атарына кіру жніндегі лт жоспары100 наты адам.docx

• атысандар мектеп малімдері Кн тртібінде Мектепте 6 Е сынып оушыларына аза тілі мен дебиеті пні бойынша айтылым дадысын жасартуда Lesson Study.docx