ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 342
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
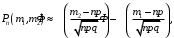где 
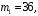
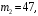
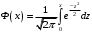– функция Лапласа (значения берутся из таблиц). Получим: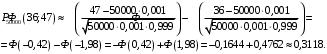
Ответ: а) 0,025; б) 0,3118.
№27
В книге на 1000 страниц 100 опечаток. Какова вероятность обнаружить, в наудачу взятой странице, хотя бы одну опечатку?
Решение
По условию задачи предполагается, что число опечаток распределено по закону Пуассона. Так как в 1000 страницах имеется 100 опечаток, поэтому можно предположить, что 1 страница содержит 1 опечатку:
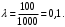
Если событие А – страница рукописи содержит хотя бы одну опечатку, то событие
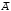– страница рукописи, не содержащая ни одной опечатки, то есть 0 опечаток. Так как число опечаток распределено по закону Пуассона, то:
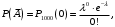где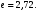 
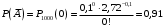
Так как события A и
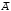противоположны, то вероятность события A равна: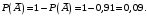
Ответ: 0,09.
№28
Радист вызывает корреспондента, причем каждый последующий вызов производится лишь в том случае, если предыдущий вызов не принят. Вероятность того, что корреспондент примет вызов, равна 0,4. Составить закон распределения числа вызовов, если число вызовов не более 5. Найти математическое ожидание и дисперсию этой случайной величины.
Решение
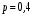– примет вызов, 
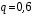– не примет вызов. Х = {1,2,3,4,5} – число вызовов, 
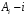– вызов принят.
Вероятность того, что первый вызов принят:
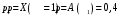
Второй вызов состоится лишь при условии, что первый вызов не принят:
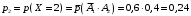
Для остальных также:
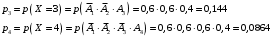
Пятый вызов при любом исходе (будет принят, не принят) – последний. Поэтому
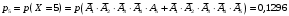
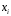 | 1 | 2 | 3 | 4 | 5 |
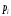 | 0,4 | 0,24 | 0,144 | 0,0864 | 0,1296 |
Проверим:
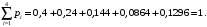
Математическое ожидание M(X) и дисперсию D(X) вычисляем по формулам:
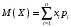и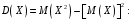 
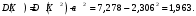
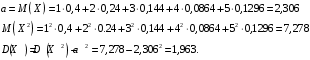
Ответ:
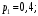
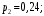
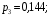
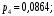
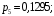
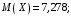
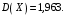
№29
Билет на электричку стоит 50 рублей, а штраф за безбилетный проезд – 450 рублей. Если безбилетник (заяц) попадается контролёру, то оплачивает и штраф, и стоимость билета. Известно, что контролёр встречается в среднем один раз на 10 поездок. Заяц ознакомился с основами теории вероятностей и решил придерживаться стратегии, которая делает математическое ожидание расходов наименьшим возможным. Как ему поступать: покупать билет каждый раз, не покупать никогда или бросать монетку – покупать билет или нет?
Решение
Пусть вероятность покупки билета p, а вероятность появления контролера q. Случайная величина X "Расходы на поездку" имеет распределение
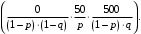
Математическое ожидание расходов:
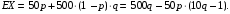
По условию
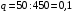. Следовательно, 
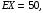то есть не зависит от р. Отсюда появляется некое "равновесие" – средний расход на поездку не зависит от частоты или вероятности покупки билета.Ответ: Всё равно.
№30
Дана функция распределения вероятностей:
Найти f(x), Р(3<Х<4), P(X<5), P(2,1
Решение
Найдем функцию плотности распределения вероятностей:
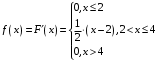
Построим графики F(x) и f(x):
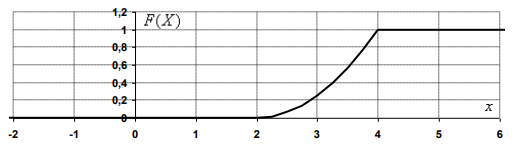
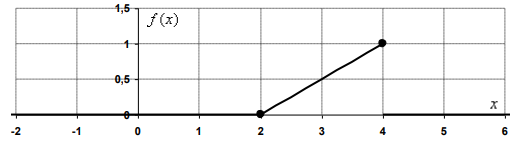
Вычислим вероятности попадания случайной величины X в интервалы:
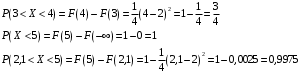
Ответ:
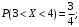
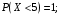
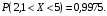
№31
Непрерывная случайная величина Х задана плотностью распределения вероятностей:
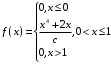
Найти
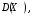
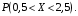
Решение
Найдем коэффициент c. По свойству функции плотности распределения:
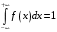
В данной задаче:
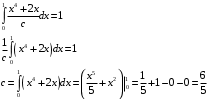
Таким образом, функция плотности распределения:
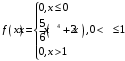
Вычислим математическое ожидание:
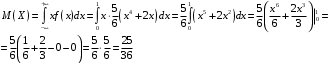
Дисперсию вычислим по формуле:
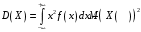
В данном случае:
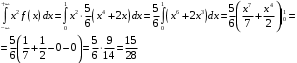
Таким образом, дисперсия:
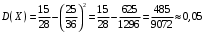
Найдем вероятность того, что случайная величина X примет значение из интервала (0,5; 2,5):
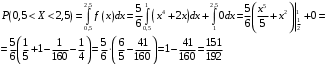
Ответ:
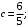
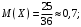
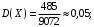
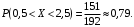
№32
Задана плотность вероятности f(x) случайной величины Х.
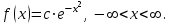
Определить:
1) коэффициент с;
2) функцию распределения F(x);
3) математическое ожидание М(Х);
4) дисперсию D(Х);
5) среднее квадратическое отклонение σ(Х);
6) вероятность попадания случайной величины Х в интервал (0;1).
Решение
Ответ: .
№33
Задана плотность вероятности f(x) случайной величины Х.
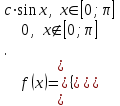
Определить:
1) коэффициент с;
2) функцию распределения F(x);
3) математическое ожидание М(Х);
4) дисперсию D(Х);
5) среднее квадратическое отклонение σ(Х);
6) вероятность попадания случайной величины Х в интервал (0;π/4).
Решение
Ответ: .
№34
В тексте учебника по психологии содержатся опечатки: в среднем, одна на десять страниц. Пусть Х – число опечаток на одной странице. Определить закон распределения для Х. Найти вероятность, что на странице есть хотя бы одна опечатка.
Решение
По условию задачи можно сделать вывод, что случайная величина Х принимает значения 0, 1, 2… и распределена по закону Пуассона с параметром
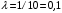(среднее число опечаток на страницу). Тогда вероятности можно находить по формуле:
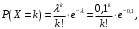где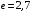 
Получаем:
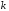 | 0 | 1 | 2 | |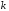
 |  |  |  |  |
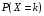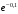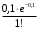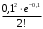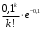Найдем вероятность, что на странице есть хотя бы одна опечатка:
