ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 344
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ответ: 0,095.
№35
Опыт состоит из трех независимых подбрасываний одновременно трех монет, каждая из которых с одинаковой вероятностью падает гербом или цифрой вверх. Построить ряд распределения, найти функцию распределения, математическое ожидание и среднее квадратичное отклонение числа одновременного выпадения двух гербов. Найти вероятность того, что два герба одновременно выпадут хотя бы один раз.
Решение
Сначала найдем вероятность p того, что при подбрасывании трех монет появится ровно 2 герба, при условии, что герб выпадает с вероятностью 0,5 и броски независимы, по формуле Бернулли:
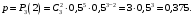
Пусть X – дискретная случайная величина, равная числу одновременного выпадения двух гербов при трех бросках трех монет. X может принимать значения 0, 1, 2 и 3. X распределена по биномиальному закону с параметрами
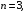
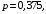поэтому вероятности будем находить по формуле Бернулли: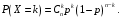 
Найдем соответствующие вероятности:
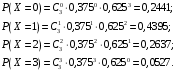
Ряд распределения случайной величины X имеет вид:
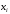 | 0 | 1 | 2 | 3 |
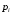 | 0,2441 | 0,4395 | 0,2637 | 0,0527 |
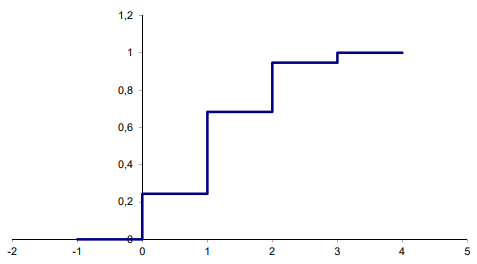
Найдём функцию распределения
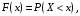то есть:при
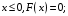
при
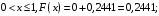
при
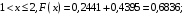
при
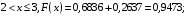
при
Построим график функции распределения:
Найдем характеристики случайной величины X. Используем известные формулы для биномиального распределения.
Математическое ожидание:
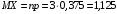
Дисперсия:
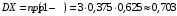
Среднее квадратичное отклонение:
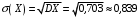
Найдем вероятность того, что два герба одновременно выпадут хотя бы один раз:
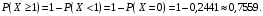
Ответ: 0,7559.
№36
Заданы математическое ожидание а=6и среднее квадратическое отклонение σ=2 нормально распределенной случайной величины X. Написать плотность распределения вероятностей и схематично построить ее график. Применяя правило «трёх сигм», найти значения случайной величины X.
Решение
Ответ: .
№37
Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Yравна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и Cov[X,Y].
Решение
Учитываем, что выпадение любого числа очков на кости равно
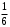и выпадения на двух костях независимы, то есть каждая комбинация вида 
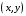выпадает с вероятностью 
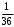(x - число очков на первой кости, y - число очков на второй кости).Запишем таблицы сумм и произведений числа очков, выделим четные комбинации:
| Сумма | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Произведение | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 |
Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. В половине случаев сумма четная, поэтому
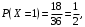
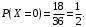
Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Получим
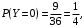
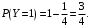
Опишем закон распределения вектора
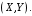
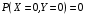(произведение и сумма нечетные).
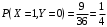(сумма четная, произведение нечетное).
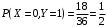(сумма нечетная, произведение четное).
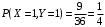(сумма четная, произведение четное).Получили закон:
| X/Y | 0 | 1 |
| 0 | 0 |  |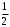
| 1 |  | |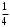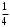
Найдём
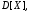
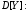
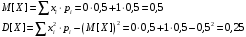
Аналогично:
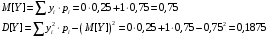
Найдем
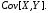Вычислим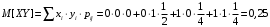
Тогда
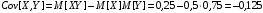
Ответ:
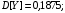
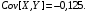
№38
Дискретная случайная величина X задана законом распределения
| X | –2 | –1 | 0 | 1 | 2 |
| Р | 0,1 | 0,2 | 0,15 | 0,25 | 0,3 |
Найти закон распределения и математическое ожидание случайной величины Y=X2.
Решение
Ответ: .
№39
Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется меньше двух.
Решение
Применим неравенство Чебышева:
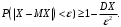
Считаем, что случайная величина X – число отказавших элементов, она распределена по биномиальному закону с параметрами
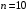(элементов), 
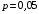(вероятность отказа элемента), 
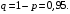Тогда можно найт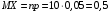и 
и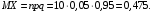 
Отклонение по условию
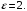
Тогда оценка вероятности того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется меньше двух, имеет вид:
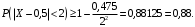
Ответ: вероятность не менее 88%.
№40