Решение

Если А играет белыми, то вероятность выигрыша 0,5

Если А играет черными, то вероятность выигрыша 0,3

Т.к. А играет и белыми, и черными, вероятность А выиграть 2 раза составит:

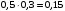
Ответ: 0,15.

№15

Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).

Решение

Вероятность того, что мишень будет поражена либо первым, либо вторым выстрелом, равна сумме вероятностей событий A и B, где A – попадание по мишени при первом выстреле; B – попадание по мишени при втором выстреле, учитывая, что при первом выстреле был промах.

Вероятность события А:

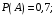
Вероятность события B:

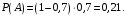
Искомая вероятность:

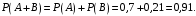
Ответ: 0,91.

№16

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Решение

Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х – хорошая, О – отличная погода). Найдем вероятности наступления такой погоды:



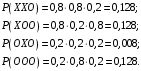
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:



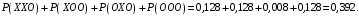
Ответ: 0,392.

№17

Известно, что на встречу выпускников Дедов придет с вероятностью p₁, Ефимов – с вероятностью p₂и Федоров – с вероятностью p₃. Выпускники приходят на встречу независимо друг от друга. Найти вероятности событий: A= {пришли только двое из названных лиц}, B = {Дедов и Ефимов пришли на встречу}, C ={хотя бы один из названных лиц пришел на встречу}.

---

Решение

---

Ответ: .

№18

В ящике 2020 носков – синих и красных. Может ли синих носков быть столько, чтобы вероятность вытащить наудачу два носка одного цвета была равна 0,5?

Решение
Ответ: .

№19

Гневные отзывы о работе интернет-магазина оставляют 80% недовольных покупателей (тех, кого плохо обслужили в магазине). Из числа довольных покупателей положительный отзыв оставляют только 15%. Некоторый интернет-магазин заработал 60 гневных и 20 положительных отзывов. Пользуясь этой статистикой, оцените вероятность того, что очередной покупатель останется доволен обслуживанием в этом интернет-магазине.

Решение

Пусть p – вероятность того, что покупателя обслужат хорошо, а 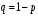вероятность того, что плохо. Тогда вероятность того, что покупатель оставит хороший отзыв, равна 0,15p, а вероятность того, что будет плохой отзыв, равна 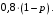Тогда:

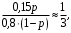откуда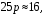

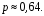
Ответ: 0,64.

№20

Имеются три одинаковых на вид урны: в первой 2 белых шара и 3 чёрных, во второй – 4 белых и один чёрный, в третьей – три белых шара. Некто подходит наугад к одной из урн и вынимает из неё один шар. Пользуясь формулой полной вероятности, Найти вероятность того, что не менее 3-х ламп из 5 останутся исправными">найти вероятность того, что этот шар будет белым.

Решение

Существует 3 гипотезы:

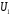– выбор первой урны: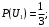

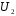– выбор второй урны: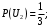

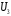– выбор третьей урны: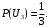

---

Интересующее нас событие А – вынутый шар окажется белым. Данное событие может произойти только с одной из гипотез:

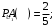
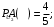
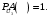Тогда: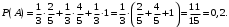

Ответ: 0,2.

№21

Радиосообщение может быть передано днем (с вероятностью 3/4), либо ночью (с вероятностью 1/4). Из-за помех вероятность его успешного приема составляет днем 60%, а ночью 80%. Найти вероятность, что сообщение будет принято.

Решение
Ответ: .

№22

Телеграфное сообщение состоит из сигналов «точка» и «тире». Статистические свойства помех таковы, что искажаются в среднем 2/5 сообщений «точка» и 1/3 сообщений «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в соотношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если:

а) принят сигнал «точка»; б) принят сигнал «тире».

Решение

Пусть событие A – принят сигнал «точка», B – принят сигнал «тире». Отсюда следует 2 гипотезы: H₁ – передан сигнал «точка», H₂ – передан сигнал «тире». По условию 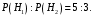Кроме того, 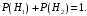Поэтому,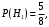

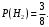
Известно, что:

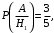
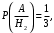
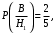
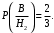
Вероятности событий A и B находим по формуле полной вероятности:



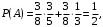
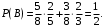
Искомые вероятности будут:

а)

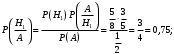
б)

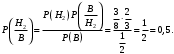
Ответ: а) 0,75; б) 0,5.


№23

Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно р₁, р₂ р₃. Вероятности того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равны: для первой кассы

---

Р₁, для второй Р₂, для третьей Р₃. Пассажир направился за билетом в одну из касс и приобрел билет. Найти вероятность того, что это была первая касса.

Решение
Ответ: .

№24

По каналу связи передается 6 сообщений. Каждое из сообщений может быть искажено помехами с вероятностью 0,2 независимо от других. Найти вероятность того, что 1) хотя бы одно сообщение из 6 искажено; 2) не более 2 из 6 не искажены; 3) все сообщения переданы без искажения.

Решение

Так как вероятность искажения 0.2, то вероятность передачи сообщения без помех – 0,8. Используя формулу Бернулли, найдем вероятность того, что:

1. 
   хотя бы одно сообщение из 6 искажено:
   

2. 
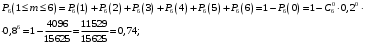
   не более 2 из 6 не искажены:
   

3. 
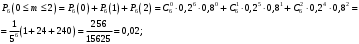
   все сообщения переданы без искажения:
   

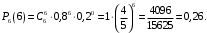
Ответ: 1) 0,74; 2) 0,02; 3) 0,26.

№25

Производится стрельба по цели тремя снарядами. Снаряды попадают в цель независимо друг от друга. Для каждого снаряда вероятность попадания в цель равна 0,4. Если в цель попал один снаряд, он поражает цель (выводит ее из строя) с вероятностью 0,3; если два снаряда – с вероятностью 0,7; если три снаряда – с вероятностью 0,9. Найти полную вероятность поражения цели.

Решение
Ответ: .

№26

Стоматологическая клиника распространяет рекламные листовки у входа в метро. Опыт показывает, что в одном случае из тысячи следует обращение в клинику. Найти вероятность того, что при распространении 50 тыс. листков число обращений будет: а) равно 41, б) находиться в границах от 36 до 47.

Решение

Имеем схему Бернулли с параметрами:

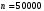– количество распространенных листовок;

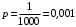– вероятность обращения в клинику после получения листовки;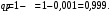



Событие А). Так как n достаточно велико, будем использовать приближенную формулу – локальную формулу Лапласа:

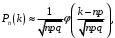где k = 41, значения функции ϕ(x) берутся из таблицы. Получим: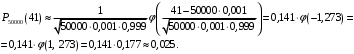



Событие Б). Так как n достаточно велико, будем использовать приближенную формулу – интегральную теорему Лапласа:

---

Смотрите также файлы

• Кн тртібі таырыбына трбие шараны жоспары. Трбие саатыны таырыбы.docx

• Фамилия Проверка читательских умений работать с текстом художественного произведения Прозрение.docx

• Lesson Study ді проблемалы сраы.docx

• Кіріспе зерттеуді зектілігі. Бгінде Елбасы Н.. Назарбаев ала ойан, дамыан отыз елді атарына кіру жніндегі лт жоспары100 наты адам.docx

• атысандар мектеп малімдері Кн тртібінде Мектепте 6 Е сынып оушыларына аза тілі мен дебиеті пні бойынша айтылым дадысын жасартуда Lesson Study.docx