Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 379
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ёмкости плоского конденсатора с диэлектриком между пластинами (d - расстояние между пластинами, S - площадь одной пластины) получим:
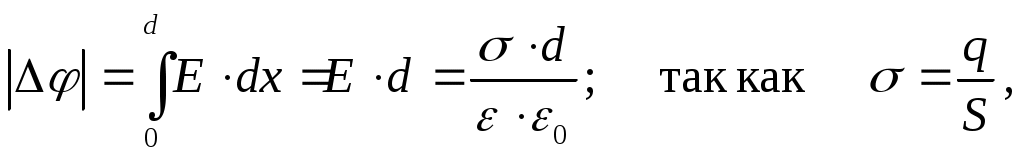 то
то 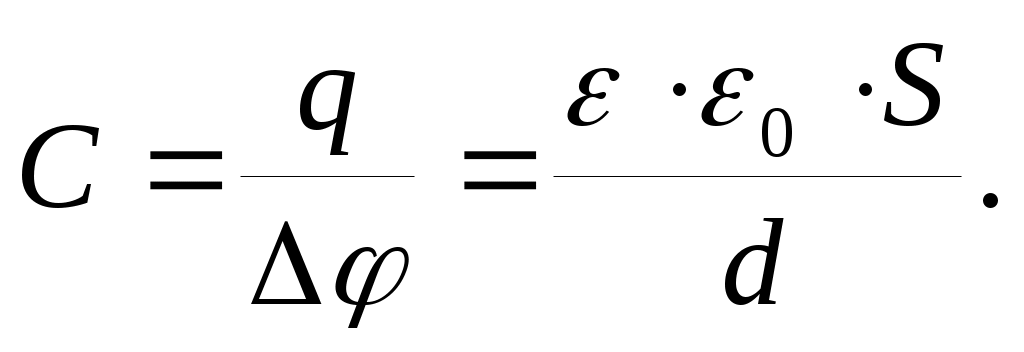
Расчет ёмкостей других конденсаторов проводится аналогично. Шаровой (сферический) конденсатор; внутренний радиус- R1, внешний - R2.
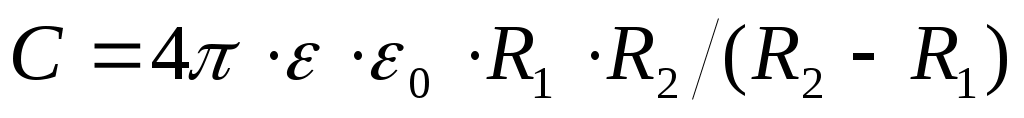 . Цилиндрический конденсатор высотой h; радиус внутреннего цилиндра - R1, внешнего - R2.
. Цилиндрический конденсатор высотой h; радиус внутреннего цилиндра - R1, внешнего - R2. 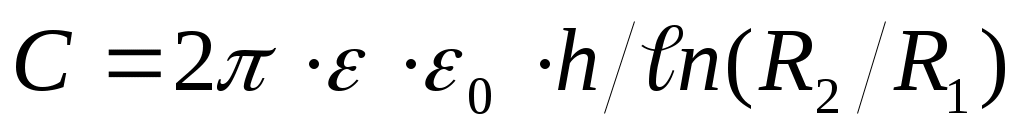 .
.
Энергия электрического поля
Электрическое поле способно совершать работу над электрическими зарядами, следовательно, оно обладает энергией (потенциальной). Вычисления проведём на примере плоского конденсатора (это удобно, так как всё поле сконденсировано между пластинами). Рассуждаем так: с помощью электрического поля перенесём все заряды с одной пластины на другую и посчитаем совершённую при этом работу. Очевидно, эта работа и будет равна запасённой (потенциальной) энергии поля в конденсаторе, ибо когда мы перенесём последний элементарный заряд, энергия израсходуется полностью, то есть само поле исчезнет. (Изменение потенциала отрицательно, работа сил поля положительна.)
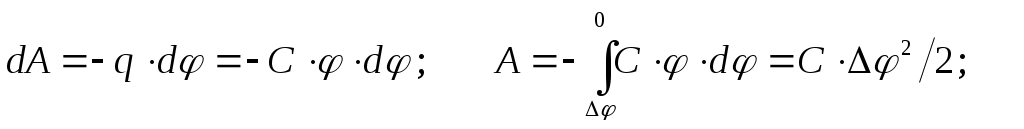
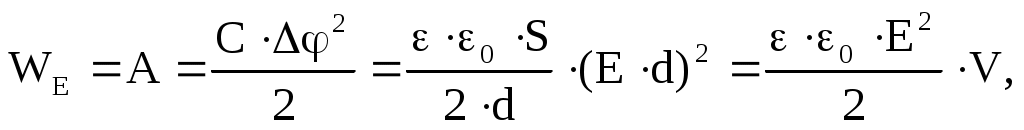
где V=S·d - объём внутри конденсатора (объём, где сосредоточено поле ). В самом общем виде энергия электрического поля, заключенная в некотором объеме V, определяется как:
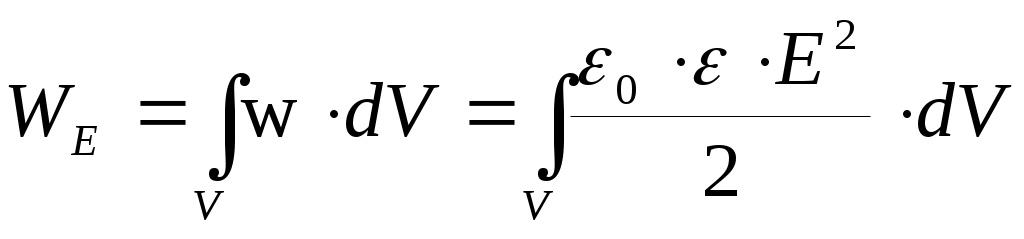 ,
,
где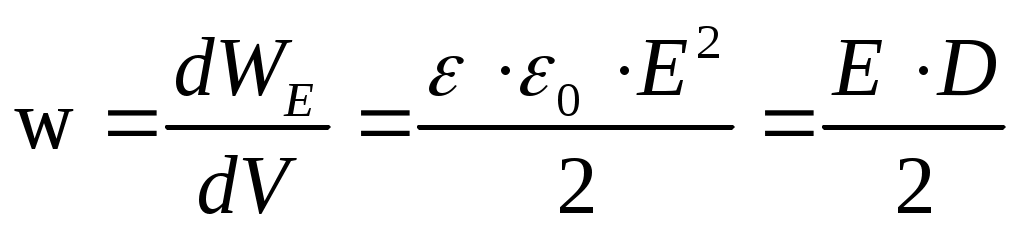 - объёмная плотность энергии электрического поля.
- объёмная плотность энергии электрического поля.
Эта формула верна всегда, для любого электрического поля Е (в том числе и для переменного).
Электрический ток Вещества, в которых есть свободные электрические заряды, называются проводниками. Все металлы являются проводниками; свободные электроны в металлах способны перемещаться по всему объёму металла. Под действием электрического поля перемещение становится направленным, возникает электрический ток. Сила электрического тока - количество заряда, пересекающего сечение проводника в единицу времени: I =dq/dt. Единица измерения силы тока – Ампер (А = Кл/с). Сила тока на единицу площади проводника, перпендикулярной направлению тока, называется плотностью тока: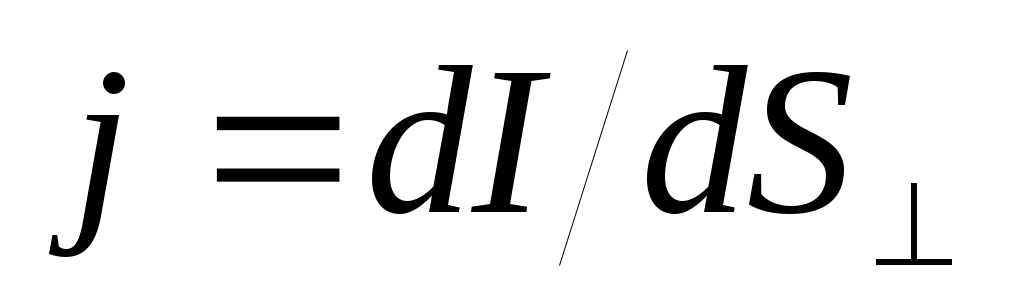 (A/м2) . Плотность тока – вектор, его направление совпадает с направлением скорости
(A/м2) . Плотность тока – вектор, его направление совпадает с направлением скорости  положительных зарядов в проводнике:
положительных зарядов в проводнике: 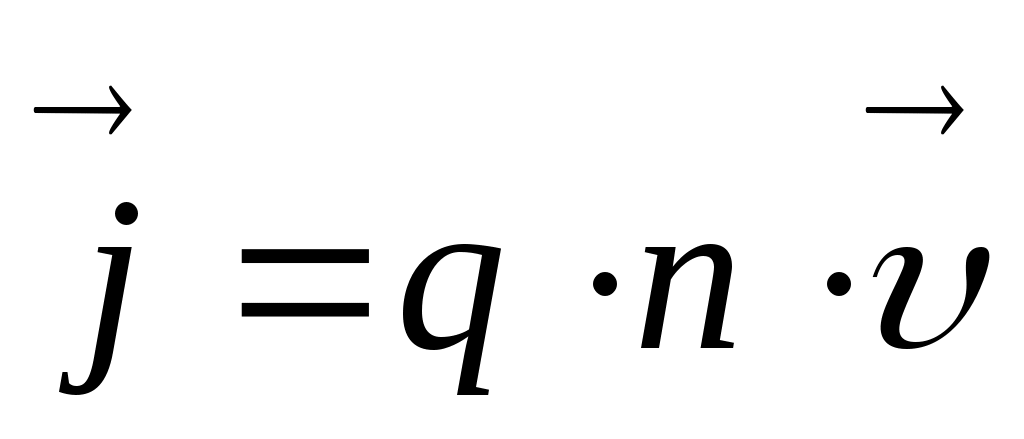 (n - концентрация зарядов). Сила тока I – скалярная величина,
(n - концентрация зарядов). Сила тока I – скалярная величина, 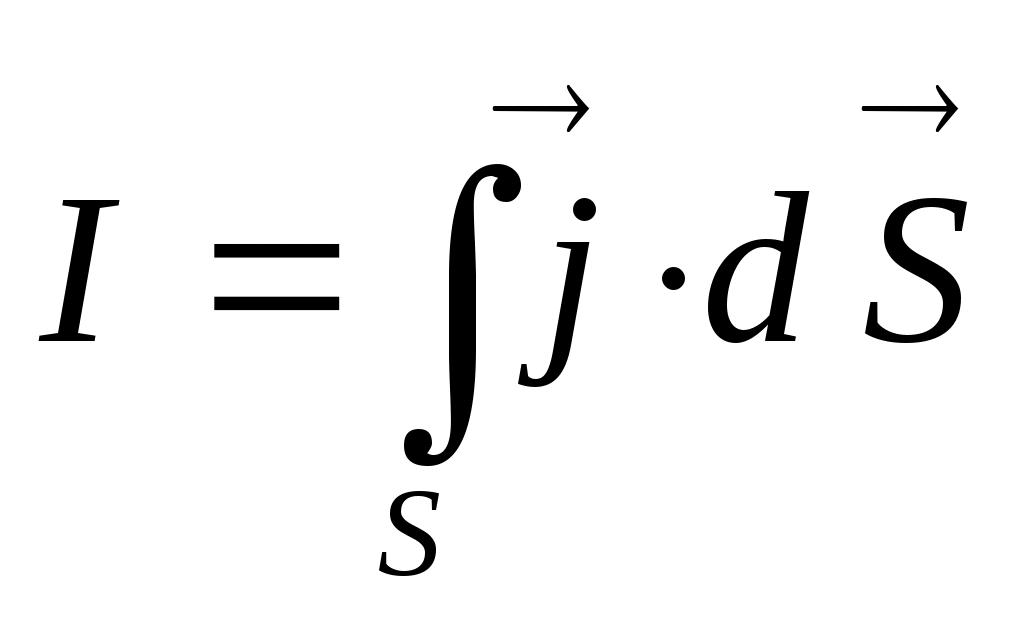 , то есть определяется через скалярное произведение векторов
, то есть определяется через скалярное произведение векторов  и
и  , при этом направление вектора
, при этом направление вектора  определяется направлением нормали к поверхности площадки dS (обычно выбирают ту нормаль, которая составляет меньший угол с вектором плотности тока
определяется направлением нормали к поверхности площадки dS (обычно выбирают ту нормаль, которая составляет меньший угол с вектором плотности тока  ). Для того, чтобы возник электрический ток, необходимо: – наличие свободных электрических зарядов, способных перемещаться под действием электрического поля; – электрическое поле.
). Для того, чтобы возник электрический ток, необходимо: – наличие свободных электрических зарядов, способных перемещаться под действием электрического поля; – электрическое поле.
Электродвижущая сила (э.д.с.)
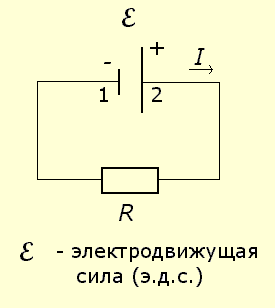
Для того, чтобы в цепи шёл постоянный ток, цепь должна быть замкнута, и что-то в этой цепи должно постоянно генерировать электрическое поле. Это "что-то" и называется электродвижущей силой (э.д.с.)
ε. Генерация поля (разности потенциалов на клеммах батареи на рисунке) осуществляется силами не электрической природы, например, за счёт химических реакций, продуктом которых является разделение зарядов, либо механическими и магнитными силами (гидро- и газогенераторы). Э.д.с. измеряется в вольтах, то есть это, по сути, не сила, а работа сторонних сил по перемещению единичного заряда против электрического поля (на рисунке положительные заряды внутри батареи должны быть перемещены от отрицательного контакта 1 к положительному 2, а во внешней цепи наоборот):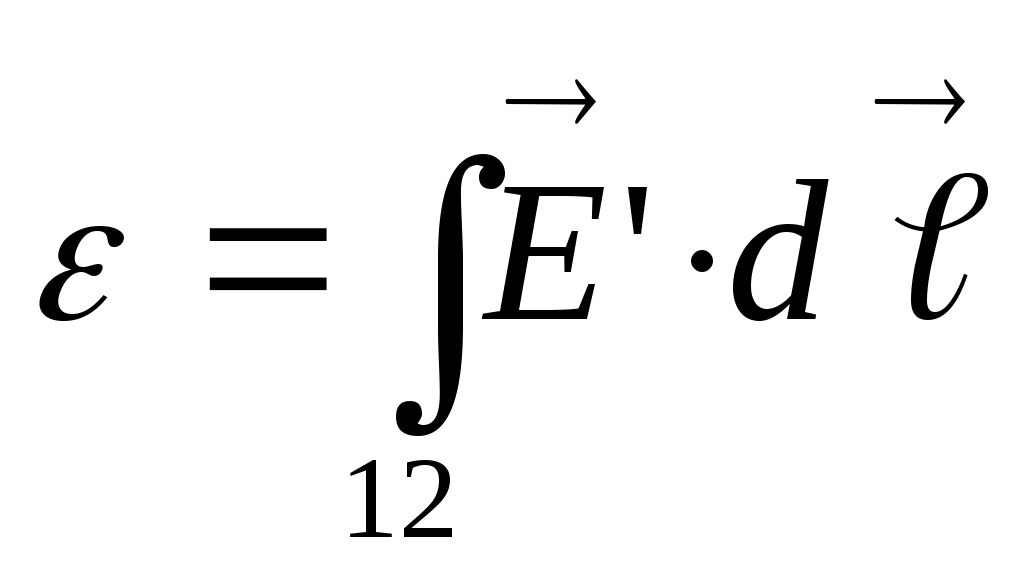 . За положительное направление тока в цепи принято направление движения положительных зарядов. Так, например, в металлических проводниках направление тока противоположно направлению движения носителей отрицательного заряда - электронов.
. За положительное направление тока в цепи принято направление движения положительных зарядов. Так, например, в металлических проводниках направление тока противоположно направлению движения носителей отрицательного заряда - электронов.
Электрическое сопротивление Носители зарядов (электроны в металлах, ионы в электролитах) при своём движении сталкиваются с молекулами вещества проводника (с ионами кристаллической решётки в металлах, с другими ионами в электролитах). Направленное движение при этом замедляется – электрический ток испытывает сопротивление. Очевидно, что общее сопротивление R зависит от сечения проводника (чем оно больше, тем сопротивление меньше), от длины проводника (чем короче, тем сопротивление меньше), от вещества проводника. Если ввести так называемое удельное сопротивление ρ, зависящее только от материала, то можно записать для электрического сопротивления цилиндрического проводника: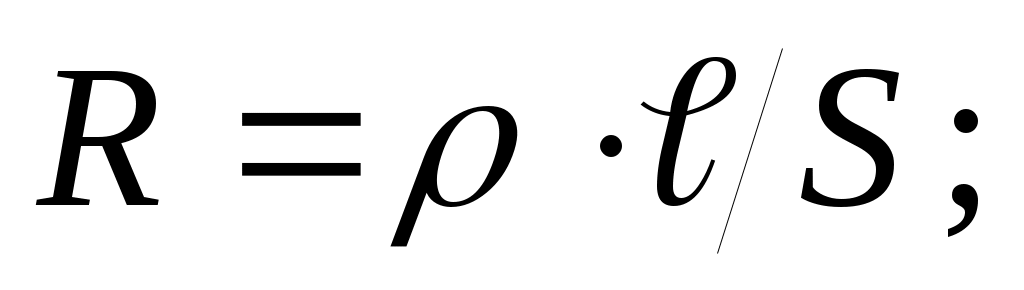 где R – сопротивление (полное) (Ом); S – сечение проводника (м2); ℓ - длина проводника (м); ρ – удельное сопротивление (Ом·м) (приводится в справочниках). В самом общем случае, когда сечение и (или) удельное сопротивление проводника изменяются вдоль проводника, сопротивление рассчитывается как:
где R – сопротивление (полное) (Ом); S – сечение проводника (м2); ℓ - длина проводника (м); ρ – удельное сопротивление (Ом·м) (приводится в справочниках). В самом общем случае, когда сечение и (или) удельное сопротивление проводника изменяются вдоль проводника, сопротивление рассчитывается как: 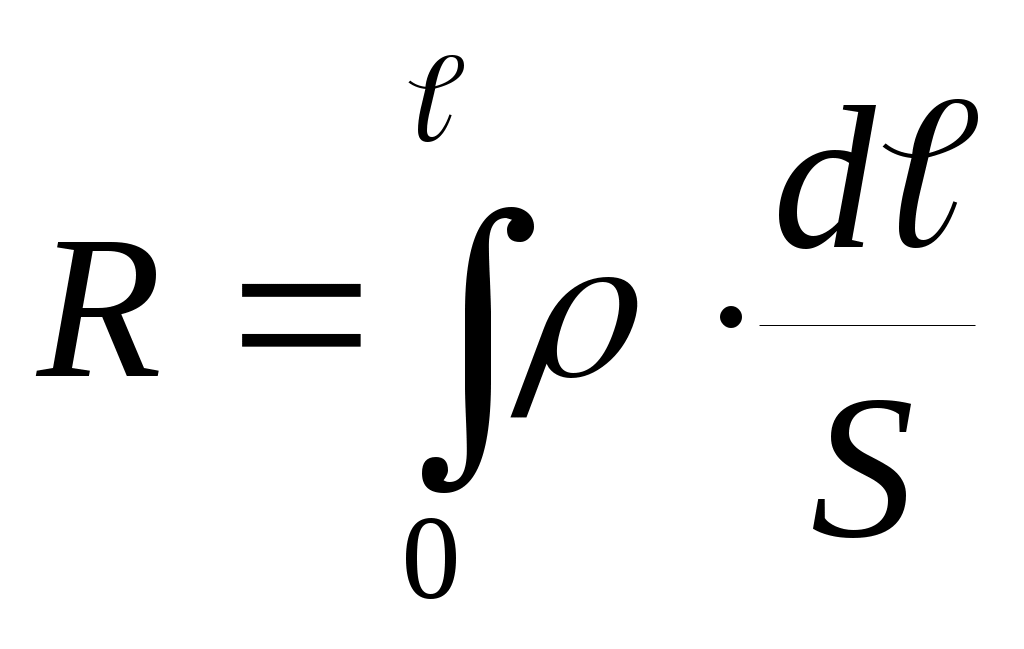 .
.
Закон Ома
В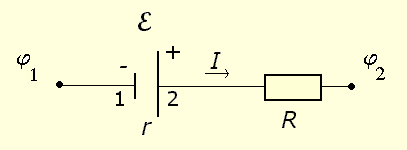 1826 г. Георг Ом экспериментально показал, что между силой тока
1826 г. Георг Ом экспериментально показал, что между силой тока
в замкнутой цепи и разностью потенциалов Δφ на концах проводника существует простая связь:
I = Δφ / R .
Если реальную электрическую цепь разомкнуть, то, естественно, ток по ней не пойдёт. Поэтому, когда говорят о законе Ома для незамкнутой цепи, имеют в виду, что из сложной электрической цепи, которая, разумеется, замкнута, и по которой идёт ток, мы выделяем незамкнутый участок и анализируем его отдельно от всей остальной цепи.
При этом вклад всех остальных, не входящих в наш участок, э.д.с. мы учитываем в виде разности потенциалов на концах нашего участка цепи: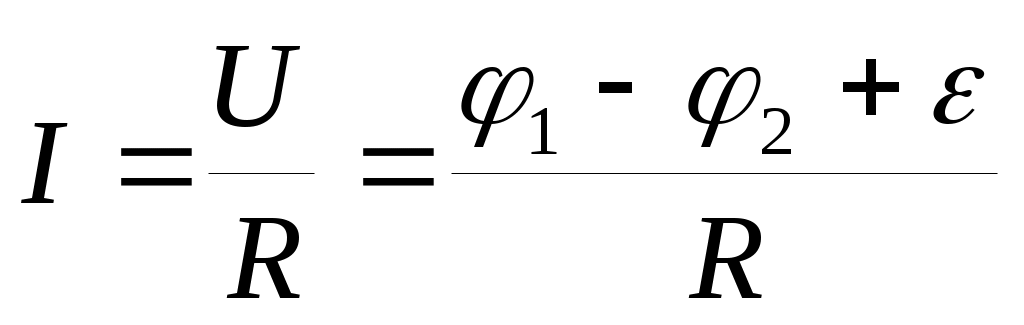 .
.
Величину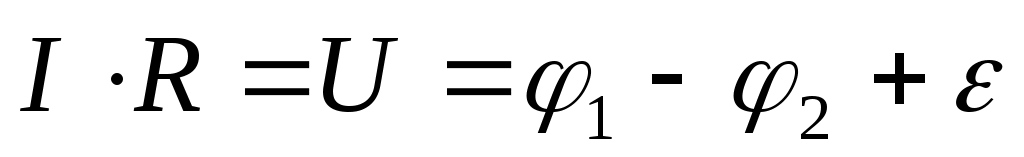 называют напряжением. Следует также отметить, что источник питания также имеет собственное сопротивлениеr, его называют внутренним сопротивлением э.д.с. . Обычно его делают малым по сравнению с внешним сопротивлением. Тем не менее, в общем случае внутреннее сопротивление r также нужно учитывать в законе Ома:
называют напряжением. Следует также отметить, что источник питания также имеет собственное сопротивлениеr, его называют внутренним сопротивлением э.д.с. . Обычно его делают малым по сравнению с внешним сопротивлением. Тем не менее, в общем случае внутреннее сопротивление r также нужно учитывать в законе Ома: 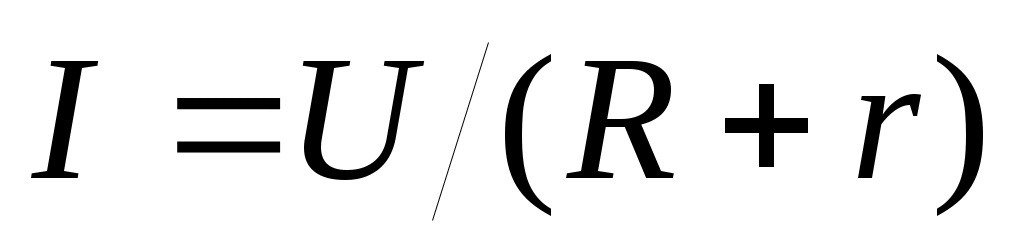 . Напряжение U для замкнутой цепи (
. Напряжение U для замкнутой цепи (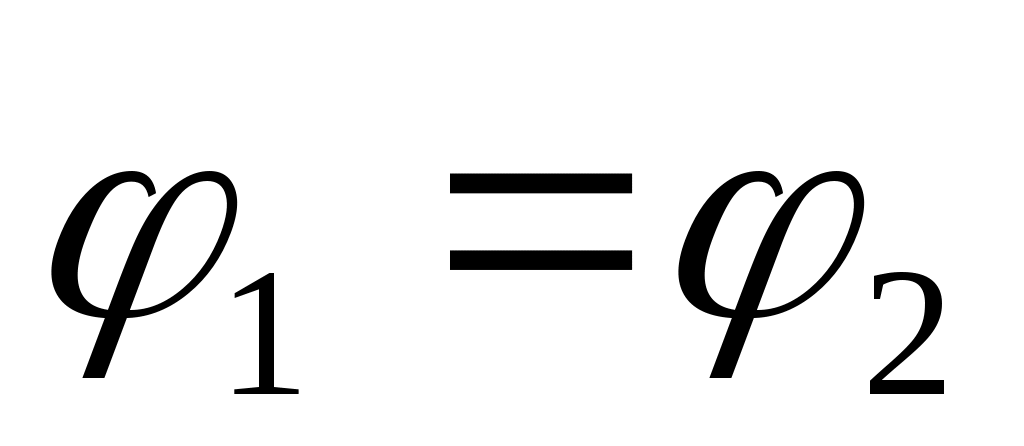 ) равно э.д.с. ε, для незамкнутой – э.д.с. плюс разность потенциалов и просто разности потенциалов, если э.д.с. отсутствует.
) равно э.д.с. ε, для незамкнутой – э.д.с. плюс разность потенциалов и просто разности потенциалов, если э.д.с. отсутствует.
Записанная выше форма закона Ома для конечного участка цепи – замкнутого или незамкнутого называется интегральной – в противоположность дифференциальной, когда закон Ома записывается для любой точки проводника (точнее, для бесконечно малой окрестности этой точки) .
Формально получить закон Ома в дифференциальной форме очень просто. Сделав в законе Ома I = U/R подстановки: I=j·S; U=E·ℓ; R=ρ·ℓ/S , придем к искомой формуле: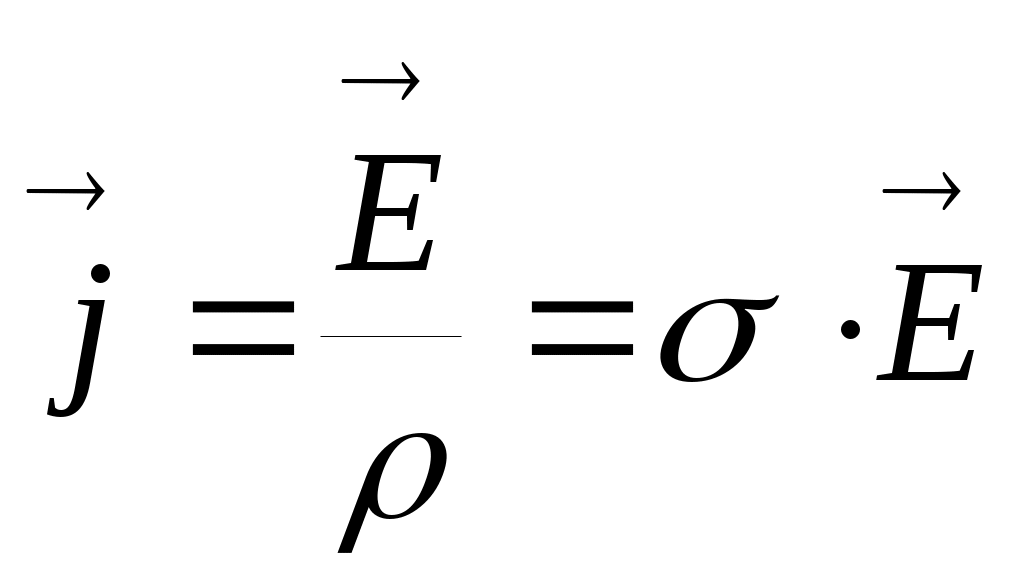 ,
,
где σ =1/ ρ – удельная проводимость вещества (Ом -1·м -1).
Т.о., сила тока I в проводнике пропорциональна напряжению U (закон Ома в интегральной форме) или плотность тока
пропорциональна напряженности электрического поля в проводнике (закон Ома в дифференциальной форме).
в проводнике (закон Ома в дифференциальной форме).
Закон Джоуля-Ленца При постоянном токе в цепи электрическое поле совершает работу, в точности равную работе сил трения (сопротивления). Последняя полностью переходит в тепловую энергию Q проводника. Приравняв количество выделяемого в проводнике тепла Q работе поля по перемещению зарядов в цепи (А=q·U=I·t.U), получим закон Джоуля-Ленца в интегральной форме:
Q = I·U·t=I2·R·t.
Работа в единицу времени называется мощностью электрического тока:
P = I·U=I2·R.
Если использовать выражения: I=j·S; R=ρ·ℓ/S; V=S·ℓ и ввести понятие удельной тепловой мощности Pуд=Q / (V·t) (Дж / c·м3=Вт / м3 ), т.е. энергии, которая выделяется в единице объема проводника за единицу времени, то получим
закон Джоуля-Ленца в дифференциальной форме: Pуд= ρ· j2= E2 / ρ=σ·E2.
Классическая теория электропроводности металлов.
В 1900 г. Друде и Лоренц предложили электронную теорию проводимости металлов, в которой совокупность свободных электронов рассматривается как некоторый идеальный газ, к которому применимы законы идеальных газов. Электроны участвуют в двух видах движения: хаотическом тепловом и направленном упорядоченном, обусловленном действием внешнего электрического поля. В электрическом поле электрон движется ускоренно и при соударении с атомом кристаллической решетки передает ему кинетическую энергию упорядоченного движения, получаемую им от поля на расстоянии свободного пробега < ℓ>, т.е., между двумя последовательными соударениями. С помощью этой теории были получены законы Ома и Джоуля-Ленца и выяснена физическая природа удельной электропроводности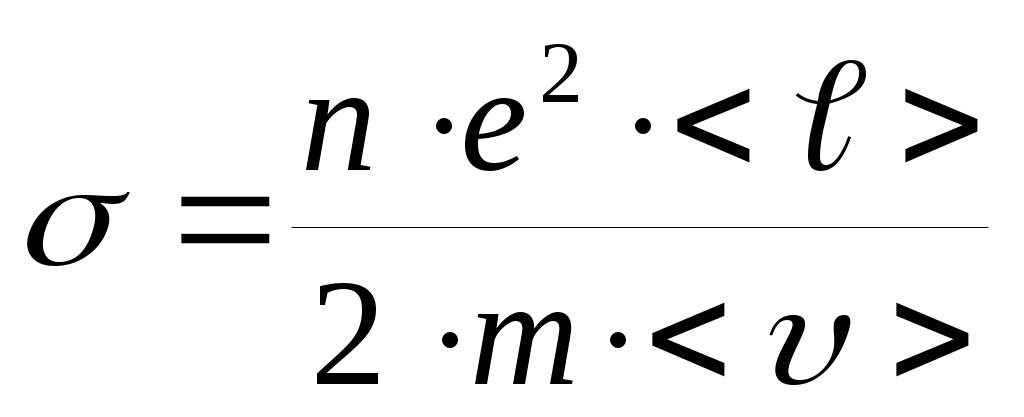 , величина которой определяется концентрацией свободных электронов n, расстоянием между атомами в металле < ℓ> и средней скоростью теплового движения <υ> электронов. Однако, теория Друде-Лоренца не смогла объяснить температурную зависимость электрического сопротивления в металлах. Действительно, если вспомнить, что
, величина которой определяется концентрацией свободных электронов n, расстоянием между атомами в металле < ℓ> и средней скоростью теплового движения <υ> электронов. Однако, теория Друде-Лоренца не смогла объяснить температурную зависимость электрического сопротивления в металлах. Действительно, если вспомнить, что
Расчет ёмкостей других конденсаторов проводится аналогично. Шаровой (сферический) конденсатор; внутренний радиус- R1, внешний - R2.
Энергия электрического поля
Электрическое поле способно совершать работу над электрическими зарядами, следовательно, оно обладает энергией (потенциальной). Вычисления проведём на примере плоского конденсатора (это удобно, так как всё поле сконденсировано между пластинами). Рассуждаем так: с помощью электрического поля перенесём все заряды с одной пластины на другую и посчитаем совершённую при этом работу. Очевидно, эта работа и будет равна запасённой (потенциальной) энергии поля в конденсаторе, ибо когда мы перенесём последний элементарный заряд, энергия израсходуется полностью, то есть само поле исчезнет. (Изменение потенциала отрицательно, работа сил поля положительна.)
где V=S·d - объём внутри конденсатора (объём, где сосредоточено поле ). В самом общем виде энергия электрического поля, заключенная в некотором объеме V, определяется как:
где
Эта формула верна всегда, для любого электрического поля Е (в том числе и для переменного).
-
ЭЛЕКТРИЧЕСКИЙ ТОК.

Электрический ток Вещества, в которых есть свободные электрические заряды, называются проводниками. Все металлы являются проводниками; свободные электроны в металлах способны перемещаться по всему объёму металла. Под действием электрического поля перемещение становится направленным, возникает электрический ток. Сила электрического тока - количество заряда, пересекающего сечение проводника в единицу времени: I =dq/dt. Единица измерения силы тока – Ампер (А = Кл/с). Сила тока на единицу площади проводника, перпендикулярной направлению тока, называется плотностью тока:
Электродвижущая сила (э.д.с.)
Для того, чтобы в цепи шёл постоянный ток, цепь должна быть замкнута, и что-то в этой цепи должно постоянно генерировать электрическое поле. Это "что-то" и называется электродвижущей силой (э.д.с.)
ε. Генерация поля (разности потенциалов на клеммах батареи на рисунке) осуществляется силами не электрической природы, например, за счёт химических реакций, продуктом которых является разделение зарядов, либо механическими и магнитными силами (гидро- и газогенераторы). Э.д.с. измеряется в вольтах, то есть это, по сути, не сила, а работа сторонних сил по перемещению единичного заряда против электрического поля (на рисунке положительные заряды внутри батареи должны быть перемещены от отрицательного контакта 1 к положительному 2, а во внешней цепи наоборот):
Электрическое сопротивление Носители зарядов (электроны в металлах, ионы в электролитах) при своём движении сталкиваются с молекулами вещества проводника (с ионами кристаллической решётки в металлах, с другими ионами в электролитах). Направленное движение при этом замедляется – электрический ток испытывает сопротивление. Очевидно, что общее сопротивление R зависит от сечения проводника (чем оно больше, тем сопротивление меньше), от длины проводника (чем короче, тем сопротивление меньше), от вещества проводника. Если ввести так называемое удельное сопротивление ρ, зависящее только от материала, то можно записать для электрического сопротивления цилиндрического проводника:
Закон Ома
В
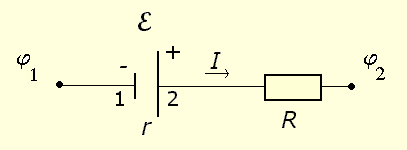 1826 г. Георг Ом экспериментально показал, что между силой тока
1826 г. Георг Ом экспериментально показал, что между силой тока
в замкнутой цепи и разностью потенциалов Δφ на концах проводника существует простая связь:
I = Δφ / R .
Если реальную электрическую цепь разомкнуть, то, естественно, ток по ней не пойдёт. Поэтому, когда говорят о законе Ома для незамкнутой цепи, имеют в виду, что из сложной электрической цепи, которая, разумеется, замкнута, и по которой идёт ток, мы выделяем незамкнутый участок и анализируем его отдельно от всей остальной цепи.
При этом вклад всех остальных, не входящих в наш участок, э.д.с. мы учитываем в виде разности потенциалов на концах нашего участка цепи:
Величину
Записанная выше форма закона Ома для конечного участка цепи – замкнутого или незамкнутого называется интегральной – в противоположность дифференциальной, когда закон Ома записывается для любой точки проводника (точнее, для бесконечно малой окрестности этой точки) .
Формально получить закон Ома в дифференциальной форме очень просто. Сделав в законе Ома I = U/R подстановки: I=j·S; U=E·ℓ; R=ρ·ℓ/S , придем к искомой формуле:
где σ =1/ ρ – удельная проводимость вещества (Ом -1·м -1).
Т.о., сила тока I в проводнике пропорциональна напряжению U (закон Ома в интегральной форме) или плотность тока
пропорциональна напряженности электрического поля
Закон Джоуля-Ленца При постоянном токе в цепи электрическое поле совершает работу, в точности равную работе сил трения (сопротивления). Последняя полностью переходит в тепловую энергию Q проводника. Приравняв количество выделяемого в проводнике тепла Q работе поля по перемещению зарядов в цепи (А=q·U=I·t.U), получим закон Джоуля-Ленца в интегральной форме:
Q = I·U·t=I2·R·t.
Работа в единицу времени называется мощностью электрического тока:
P = I·U=I2·R.
Если использовать выражения: I=j·S; R=ρ·ℓ/S; V=S·ℓ и ввести понятие удельной тепловой мощности Pуд=Q / (V·t) (Дж / c·м3=Вт / м3 ), т.е. энергии, которая выделяется в единице объема проводника за единицу времени, то получим
закон Джоуля-Ленца в дифференциальной форме: Pуд= ρ· j2= E2 / ρ=σ·E2.
Классическая теория электропроводности металлов.
В 1900 г. Друде и Лоренц предложили электронную теорию проводимости металлов, в которой совокупность свободных электронов рассматривается как некоторый идеальный газ, к которому применимы законы идеальных газов. Электроны участвуют в двух видах движения: хаотическом тепловом и направленном упорядоченном, обусловленном действием внешнего электрического поля. В электрическом поле электрон движется ускоренно и при соударении с атомом кристаллической решетки передает ему кинетическую энергию упорядоченного движения, получаемую им от поля на расстоянии свободного пробега < ℓ>, т.е., между двумя последовательными соударениями. С помощью этой теории были получены законы Ома и Джоуля-Ленца и выяснена физическая природа удельной электропроводности
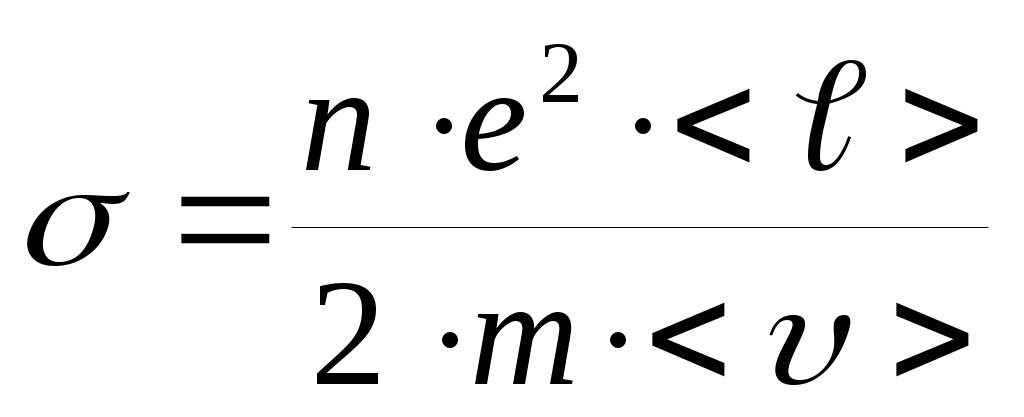 , величина которой определяется концентрацией свободных электронов n, расстоянием между атомами в металле < ℓ> и средней скоростью теплового движения <υ> электронов. Однако, теория Друде-Лоренца не смогла объяснить температурную зависимость электрического сопротивления в металлах. Действительно, если вспомнить, что
, величина которой определяется концентрацией свободных электронов n, расстоянием между атомами в металле < ℓ> и средней скоростью теплового движения <υ> электронов. Однако, теория Друде-Лоренца не смогла объяснить температурную зависимость электрического сопротивления в металлах. Действительно, если вспомнить, что