Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 385
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Взаимодействие зарядов. Известно, что одноименные заряды отталкиваются, разноименные - притягиваются. Закон взаимодействия точечных зарядов впервые сформулировал Кулон в 1785 г. (закон Кулона) : 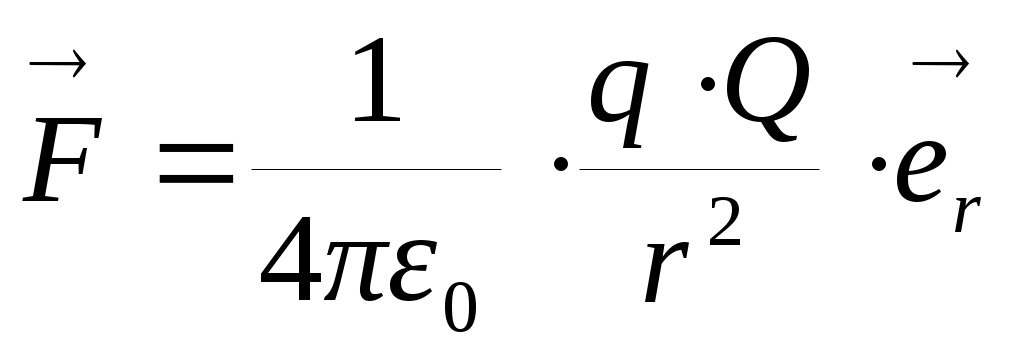 , где q, Q - взаимодействующие заряды,
, где q, Q - взаимодействующие заряды, 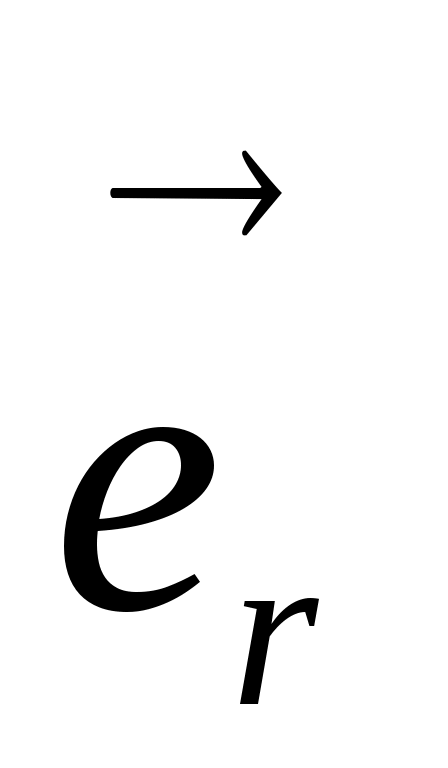 -единичный вектор в направлении радиус-вектора
-единичный вектор в направлении радиус-вектора  , r - расстояние между зарядами; сила направлена вдоль прямой, соединяющей заряды. ε0 = 8.85·10-12 Ф/м – электрическая постоянная.
, r - расстояние между зарядами; сила направлена вдоль прямой, соединяющей заряды. ε0 = 8.85·10-12 Ф/м – электрическая постоянная.
Электрическое поле .
Запишем закон Кулона в виде: 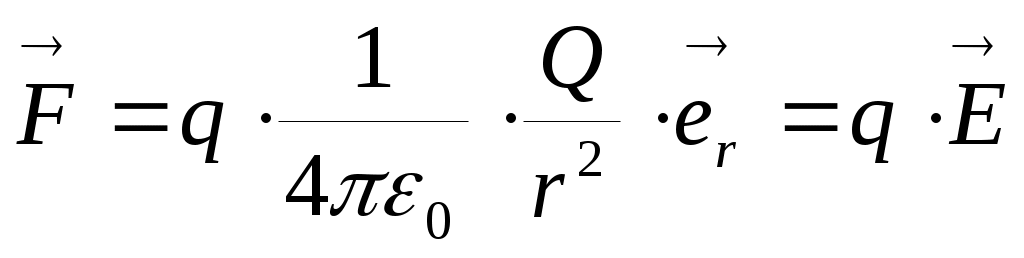 . Теперь его можно прочитать так: сила взаимодействия двух зарядов равна произведению первого заряда q на нечто, что зависит только от второго заряда Q и от расстояния до него. Это нечто и называется электрическим полем заряда Qили - более строго - напряжённостью
. Теперь его можно прочитать так: сила взаимодействия двух зарядов равна произведению первого заряда q на нечто, что зависит только от второго заряда Q и от расстояния до него. Это нечто и называется электрическим полем заряда Qили - более строго - напряжённостью 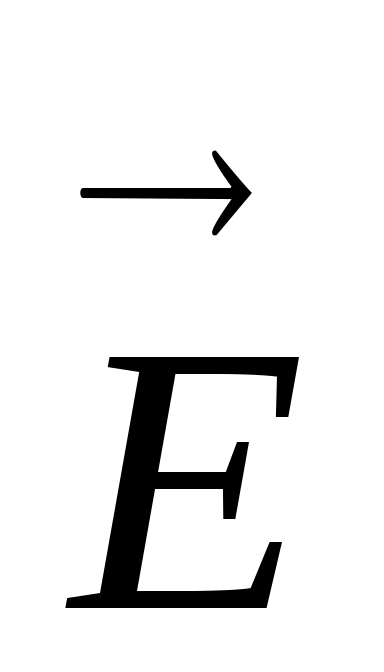 электрического поля, создаваемого зарядом Q. Напряженность– векторная характеристика электрического поля, численно равная силе, с которой поле действует на единичный электрический заряд, помещенный в рассматриваемую точку поля:
электрического поля, создаваемого зарядом Q. Напряженность– векторная характеристика электрического поля, численно равная силе, с которой поле действует на единичный электрический заряд, помещенный в рассматриваемую точку поля: 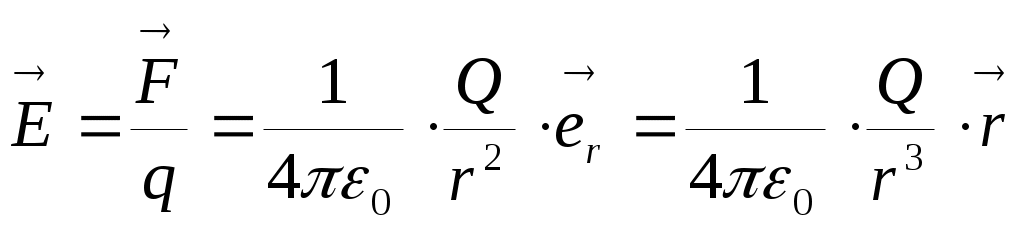 .
.
(Поле не просто удобный математический способ описания взаимодействия, а еще одна форма существования материи (наряду с веществом); о его наличии мы судим по силовому воздействию на пробные тела).
Если заряд q взаимодействует с несколькими зарядами, можно сказать, что он взаимодействует с электрическим полем, созданным этими зарядами, при этом электрическое поле вычисляется как векторная сумма полей от каждого заряда (принцип суперпозиции): 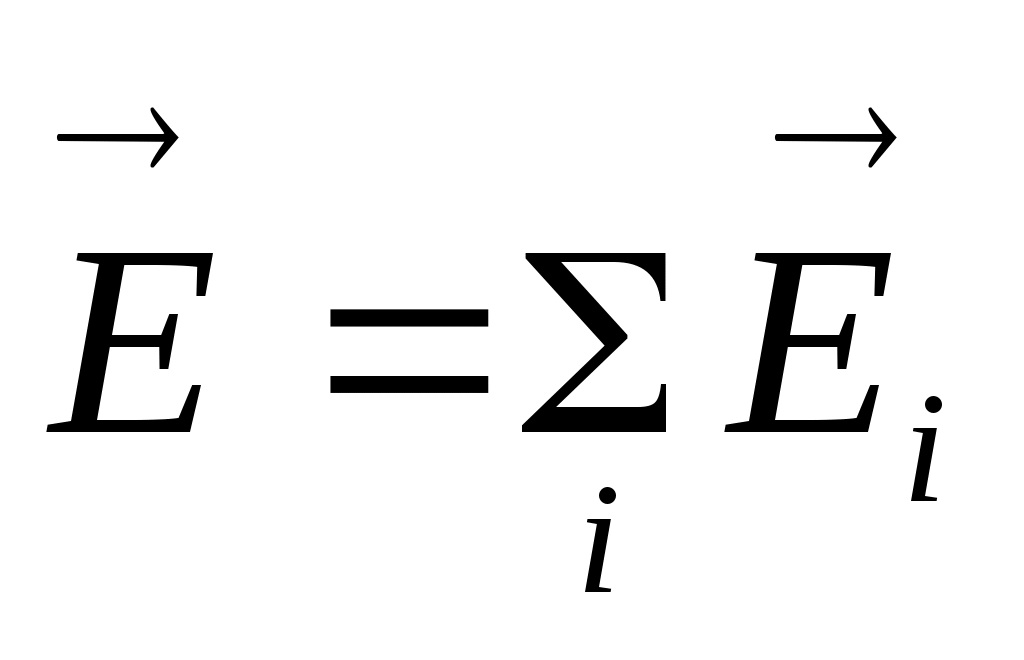 .
.
Потенциал Электростатическое поле - консервативное силовое поле, то есть работа сил поля A над зарядом q не зависит от траектории движения заряда, а определяется его начальным и конечным положениями. Работу сил такого поля при перемещении заряда q можно представить как разность некоторой функции координат U(r) в начальном и конечном положениях заряда. (Эту функцию координат U(r) называют потенциальной энергией взаимодействия зарядов).
Найдём работу А, совершаемую полем, созданным точечным зарядом Q, при перемещениизаряда q из точки 1 в точку 2:
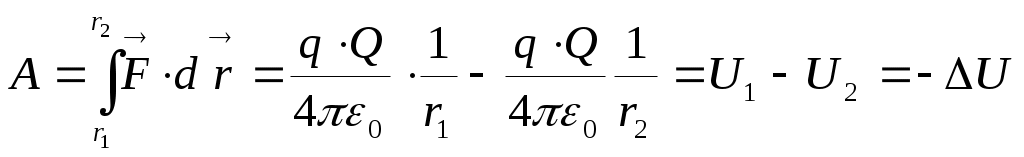 .
.
Потенциальной энергией взаимодействия зарядов q и Q будет : 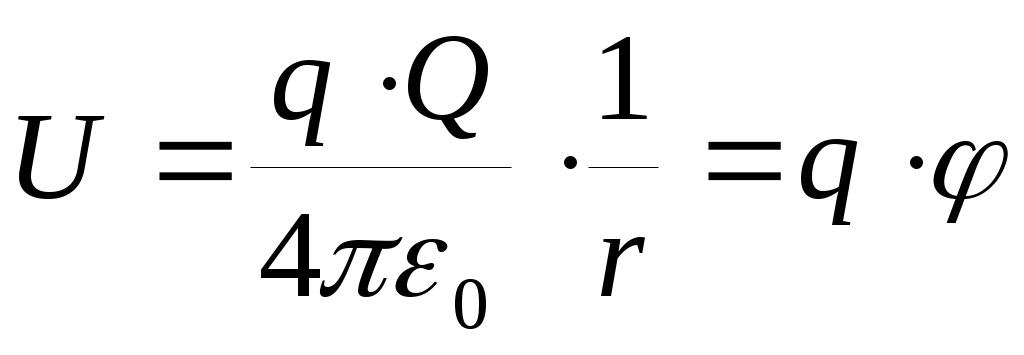 , где величина
, где величина 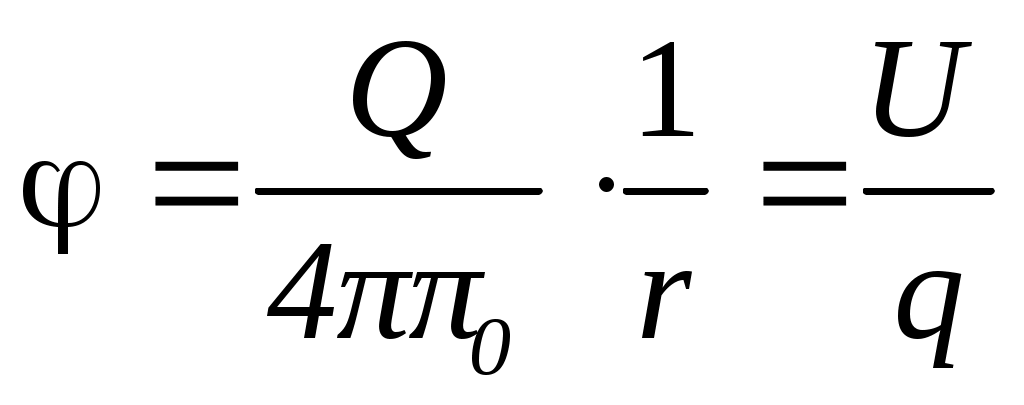 – называется потенциалом точечного заряда Q в точке пространства на расстоянии r от него.
– называется потенциалом точечного заряда Q в точке пространства на расстоянии r от него.
Потенциал φ - это скалярная характеристика электростатического поля, численно равная потенциальной энергии единичного заряда, помещенного в данную точку поля.
В системе единиц СИ напряженность измеряется в Н/Кл=В/м, а потенциал в Дж/Кл=В (Вольт).
Связь напряженности электрического поля и потенциала.
Теорема о циркуляции вектора 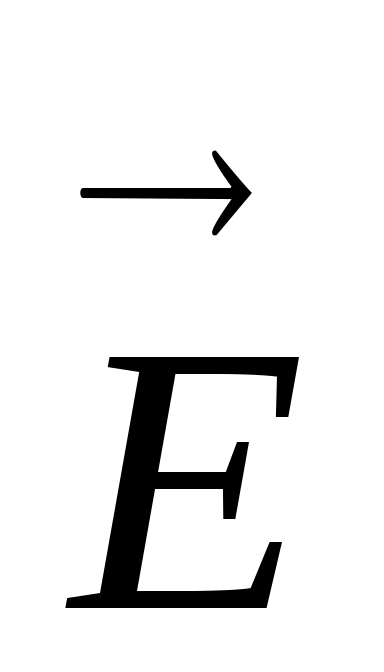 .
.
И напряжённость и потенциал описывают один объект – электростатическое поле. Найдем связь между ними, исходя из выражения для работы в дифференциальной форме: 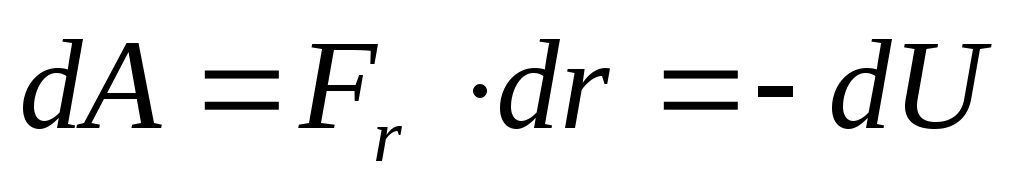 .
.
Если поделить это выражение на величину пробного заряда q, то получим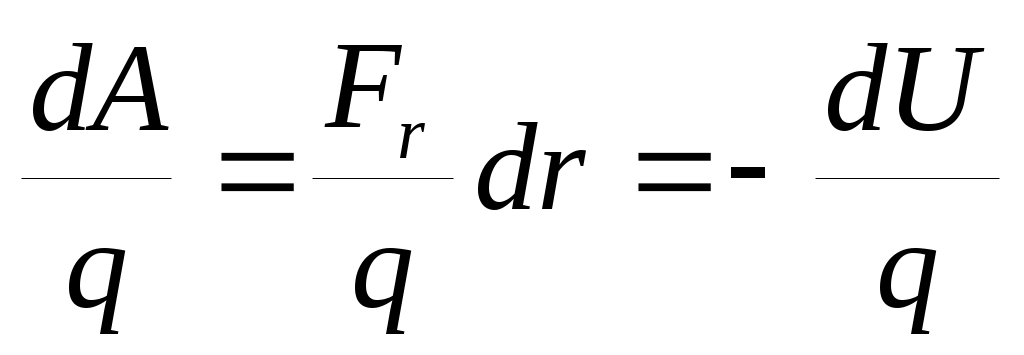 или
или 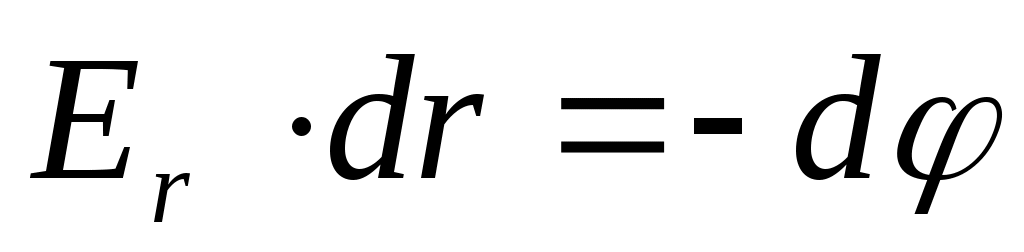 или
или 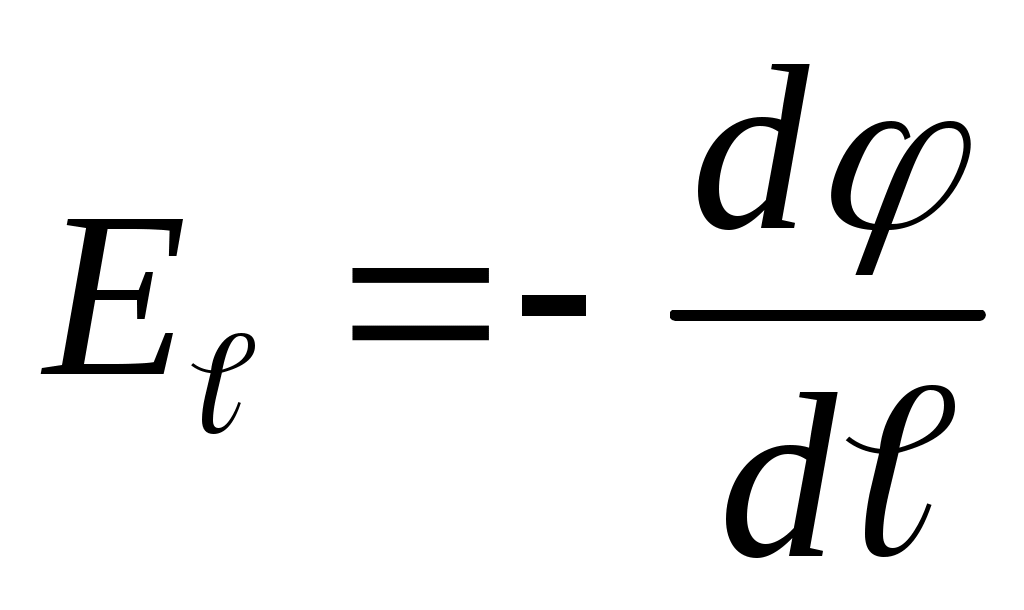 для одномерного случая. В общем виде это выражение записывается как:
для одномерного случая. В общем виде это выражение записывается как: 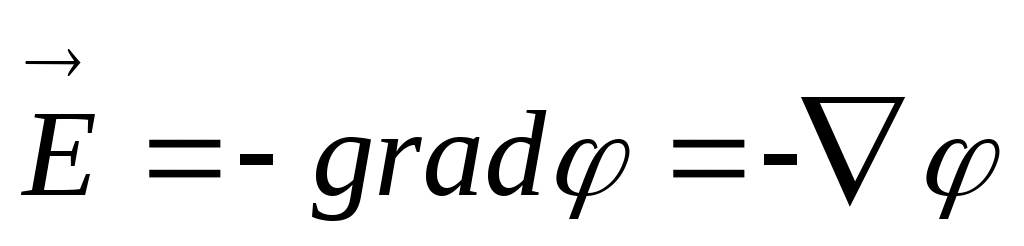 (произносится так: «напряженность поля
(произносится так: «напряженность поля 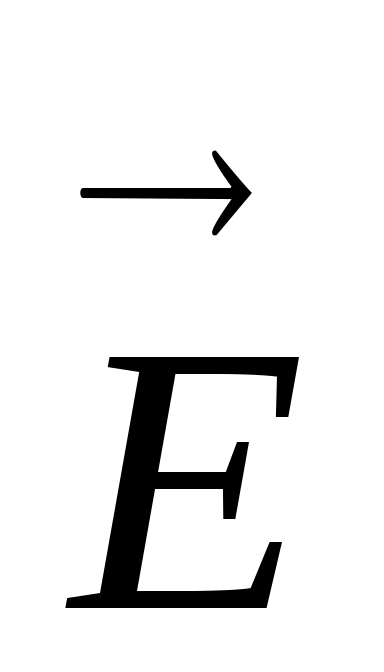 равна со знаком минус градиенту потенциала φ») , где
равна со знаком минус градиенту потенциала φ») , где 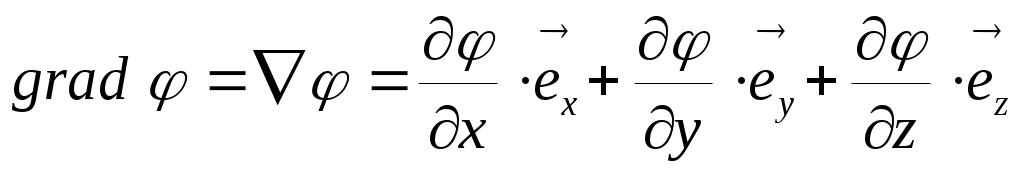 . Можно также вычислить разность потенциалов двух точек поля:
. Можно также вычислить разность потенциалов двух точек поля: 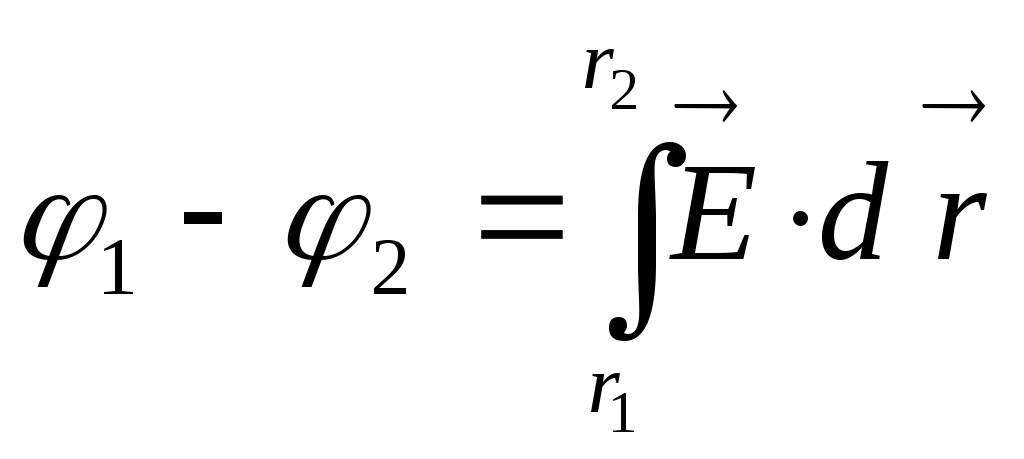 . Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность:
. Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность: 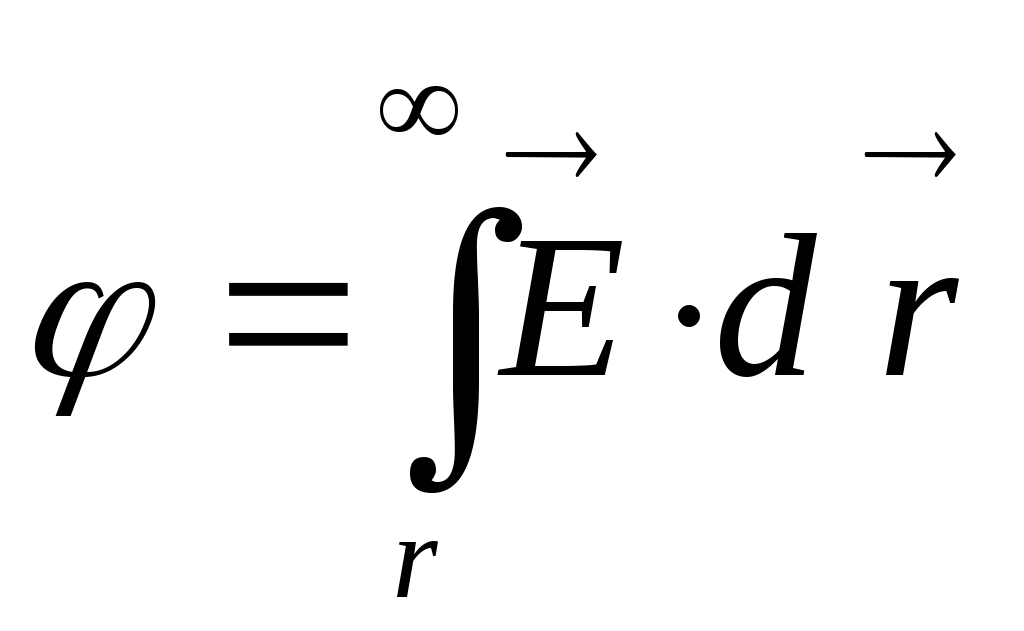 . Если единичный заряд возвращается в начальную точку, то работа электростатических сил по замкнутому контуру равна нулю:
. Если единичный заряд возвращается в начальную точку, то работа электростатических сил по замкнутому контуру равна нулю: 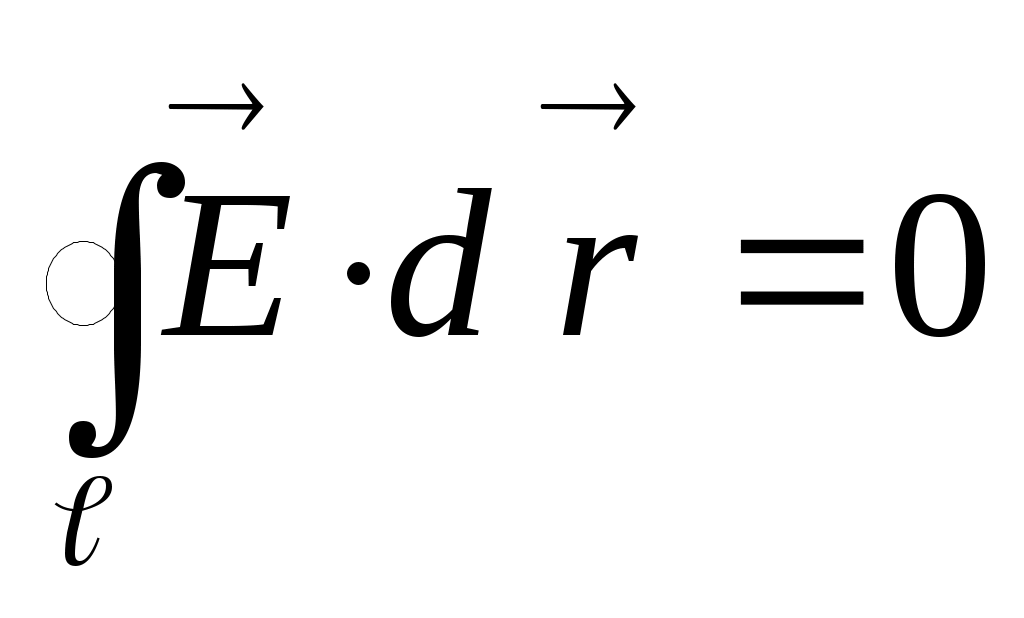 . Это соотношение носит название теоремы о циркуляции, а сам интеграл
. Это соотношение носит название теоремы о циркуляции, а сам интеграл 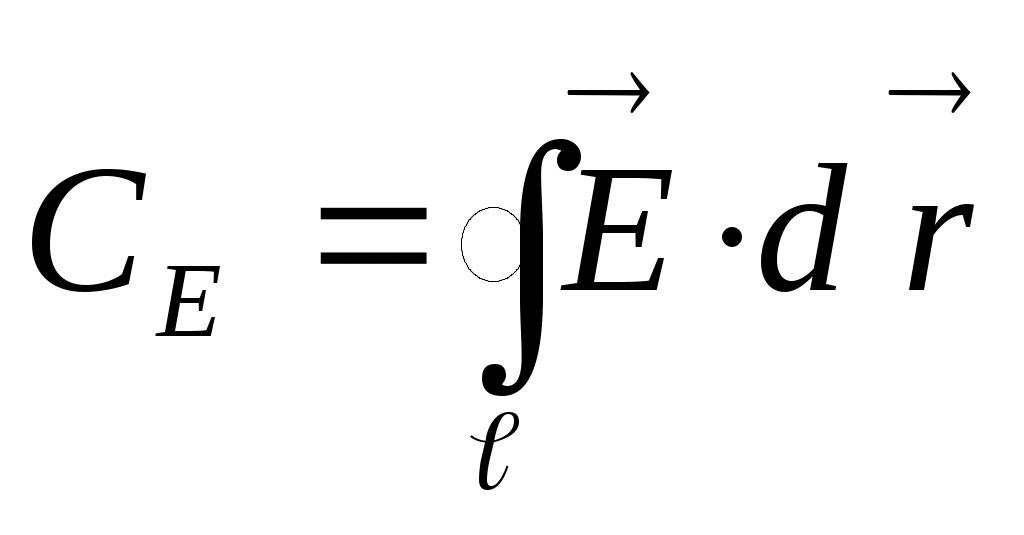 называется циркуляцией вектора
называется циркуляцией вектора 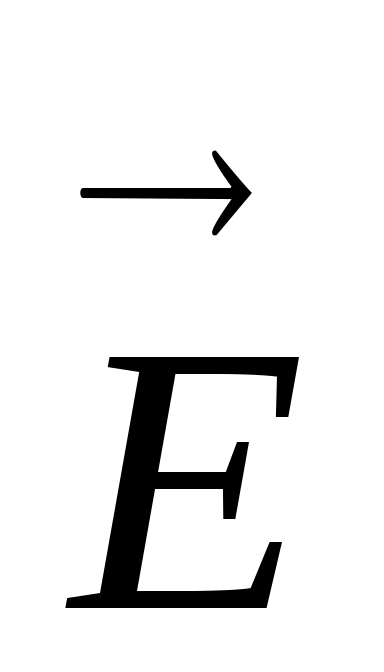 по замкнутому контуру ℓ.
по замкнутому контуру ℓ.
Линии поля
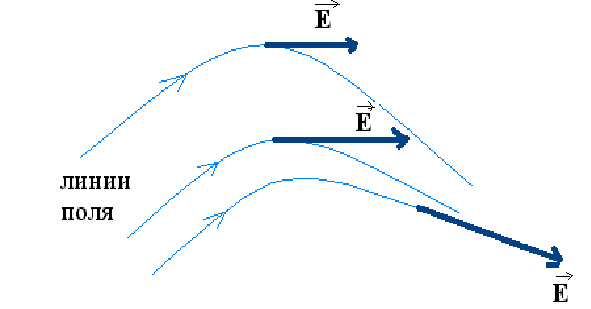
Для наглядности принято изображать векторное электрическое поле в пространстве (или на плоскости) с помощью линий электрического поля, которые строятся по следующим правилам: - вектор электрического поля 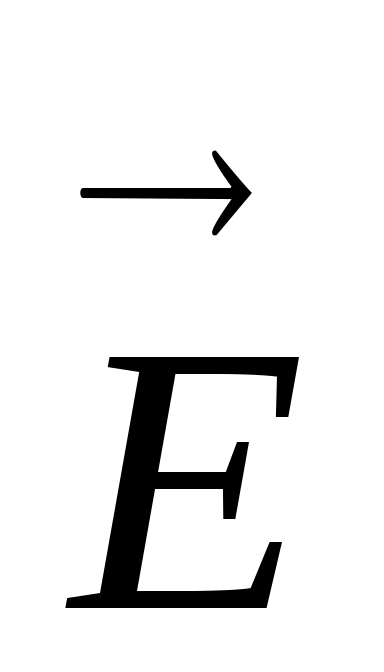 в каждой точке
в каждой точке
пространства направлен по касательной к линии поля в этой точке; - направление вектора поля 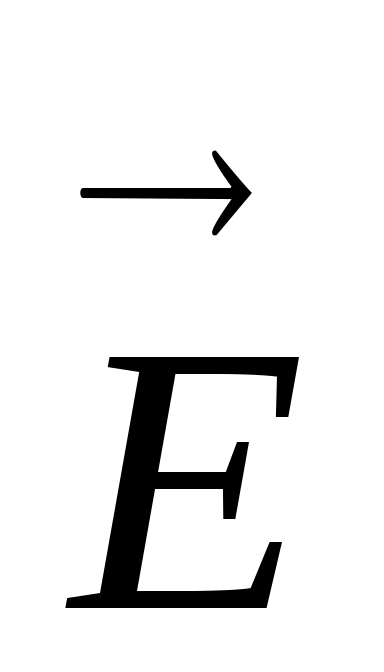 совпадает с направлением линии поля; - густота линий поля отражает величину вектора поля в данной области
совпадает с направлением линии поля; - густота линий поля отражает величину вектора поля в данной области
пространства; - линии поля начинаются на положительных зарядах и кончаются на
отрицательных; либо приходят из бесконечности и уходят в бесконечность; - поскольку в каждой точке пространства поле определено однозначно, линии поля
не могут пересекаться.
Эквипотенциальные поверхности Г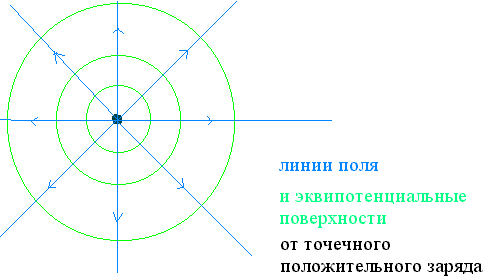 еометрическое место точек в пространстве, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью (на плоскости - эквипотенциальной линией). Из связи между вектором электрического поля и потенциалом следует, что эквипотенциальные поверхности всегда перпендикулярны линиям электрического поля. Действительно, если две точки на расстоянии dr имеют одинаковые потенциалы (т.е., dφ=0), то из соотношения dφ = - E·dr·cosα = 0, следует, что вектор
еометрическое место точек в пространстве, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью (на плоскости - эквипотенциальной линией). Из связи между вектором электрического поля и потенциалом следует, что эквипотенциальные поверхности всегда перпендикулярны линиям электрического поля. Действительно, если две точки на расстоянии dr имеют одинаковые потенциалы (т.е., dφ=0), то из соотношения dφ = - E·dr·cosα = 0, следует, что вектор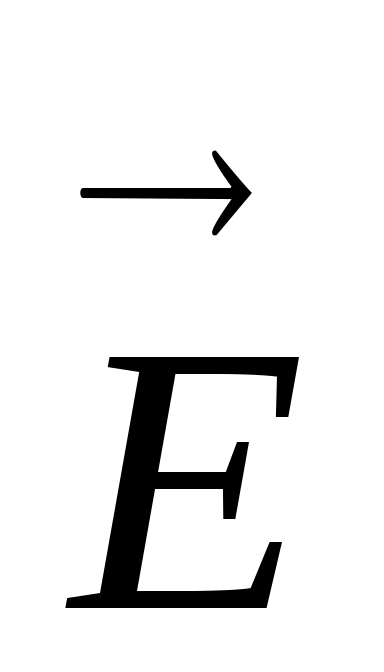 и вектор
и вектор  , соединяющий две точки на эквипотенциали, взаимно перпендикулярны (α=900). Если между соседними поверхностями одинаковая разность потенциалов, то густота эквипотенциалей, как и густота линий поля, будет отражать величину электрического поля в пространстве.
, соединяющий две точки на эквипотенциали, взаимно перпендикулярны (α=900). Если между соседними поверхностями одинаковая разность потенциалов, то густота эквипотенциалей, как и густота линий поля, будет отражать величину электрического поля в пространстве.
Теорема Гаусса Потоком напряжённости электрического поля (или просто потоком электрического поля) dФ в вакууме через площадку dS называется величина: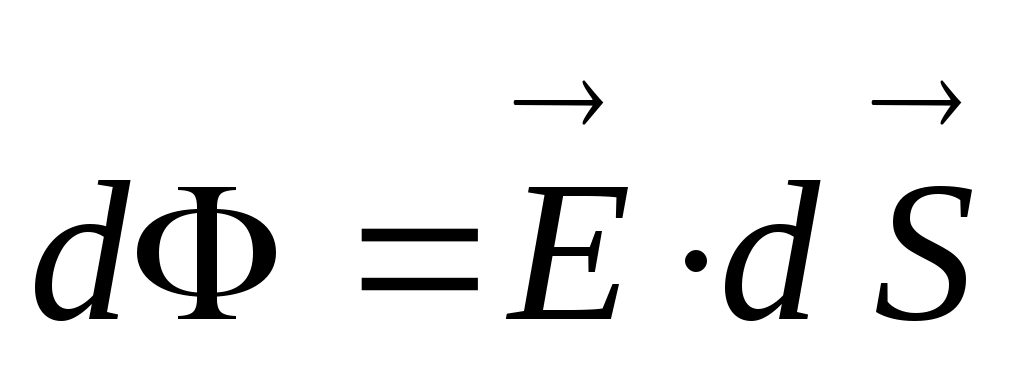 . Вектор площади
. Вектор площади 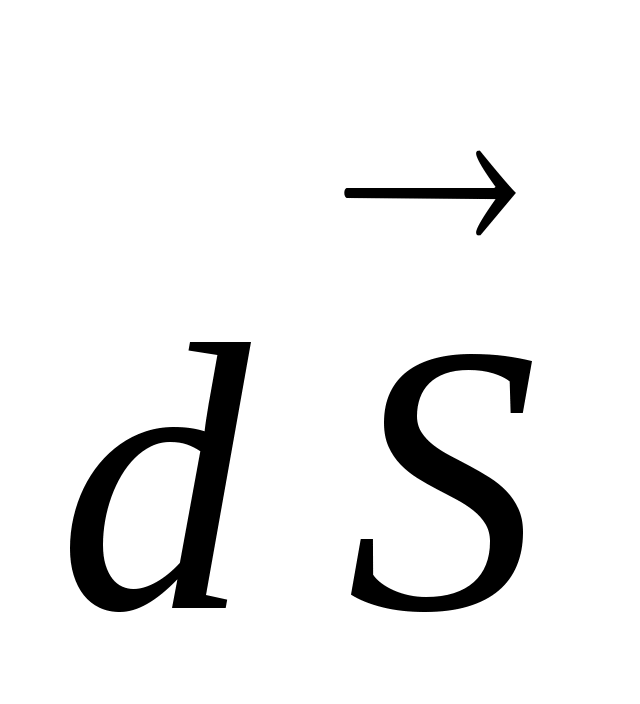 направлен по нормали к её поверхности, а его модуль равен площади площадки dS. (У площадки две стороны, поэтому всегда надо оговаривать, какую нормаль принимать за положительную) . Рассчитаем поток вектора
направлен по нормали к её поверхности, а его модуль равен площади площадки dS. (У площадки две стороны, поэтому всегда надо оговаривать, какую нормаль принимать за положительную) . Рассчитаем поток вектора 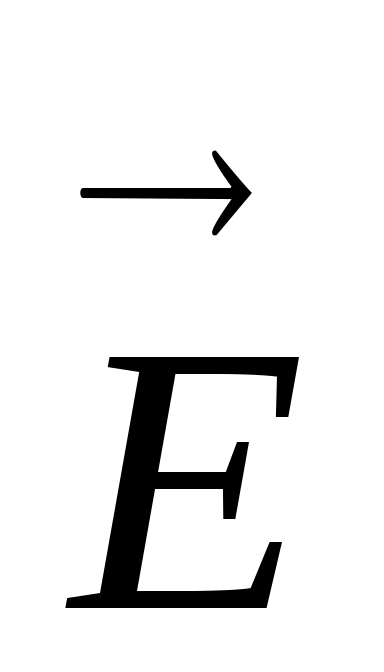 через сферическую поверхность радиусаr для поля, создаваемого точечным зарядом q, находящимся внутри этой поверхности :
через сферическую поверхность радиусаr для поля, создаваемого точечным зарядом q, находящимся внутри этой поверхности : 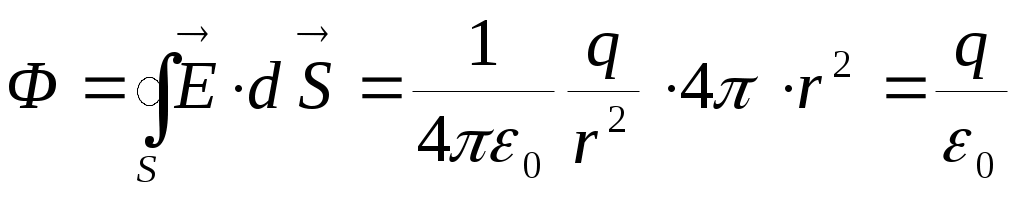 . Этот результат оказывается справедливым для замкнутой поверхности произвольной формы и для любого количества зарядов внутри такой поверхности и получил название теоремы Гаусса для электростатического поля в вакууме. Теорема Гаусса: поток вектора напряжённости электростатического поля сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов
. Этот результат оказывается справедливым для замкнутой поверхности произвольной формы и для любого количества зарядов внутри такой поверхности и получил название теоремы Гаусса для электростатического поля в вакууме. Теорема Гаусса: поток вектора напряжённости электростатического поля сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов 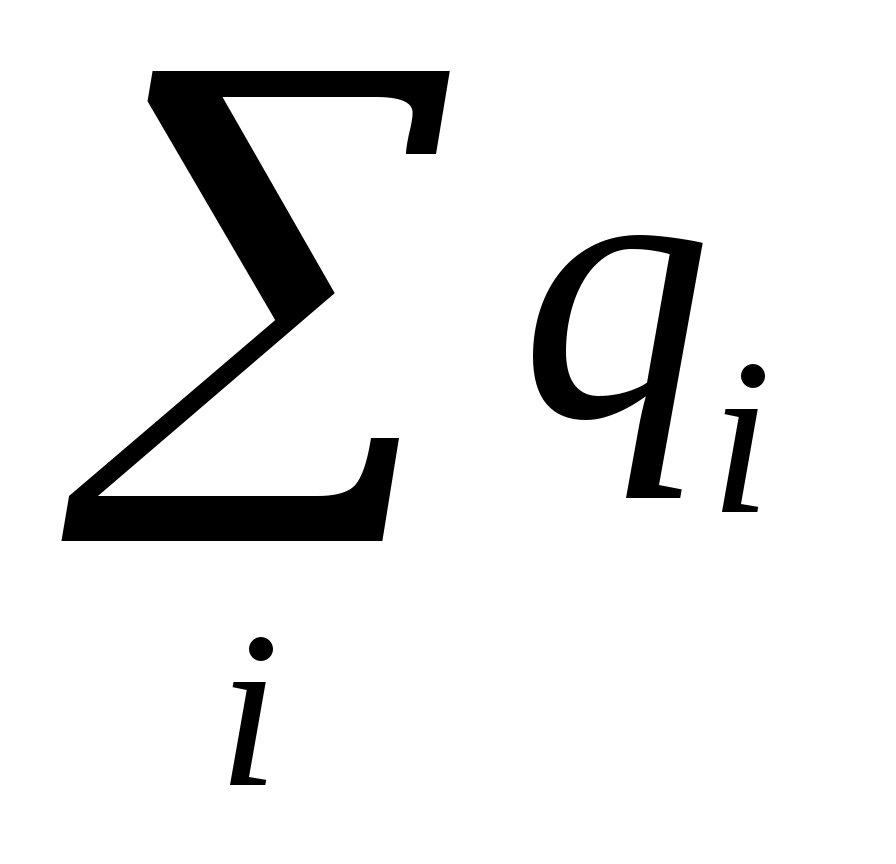 , охватываемых поверхностью S, деленной на электрическую постоянную ε0:
, охватываемых поверхностью S, деленной на электрическую постоянную ε0: 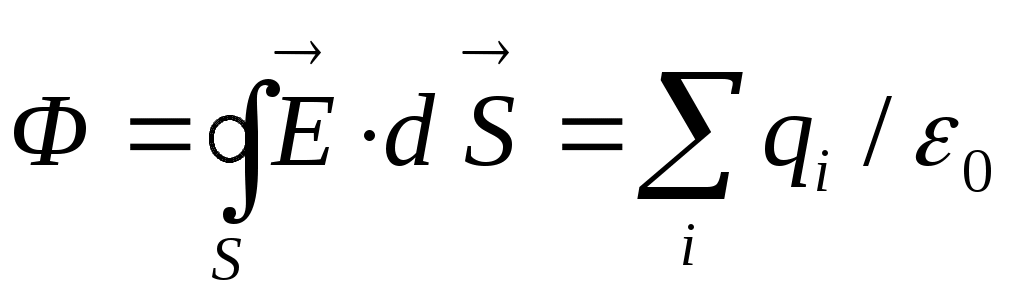 .
.
.
Н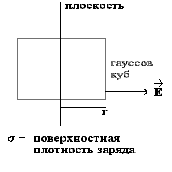
апряженность и потенциал поля заряженной плоскости Для вычисления поля, создаваемого бесконечной заряженной плоскостью, воспользуемся теоремой Гаусса, и в качестве гауссовой поверхности выберем куб со стороной 2r. Очевидно, что линии поля направлены перпендикулярно влево и вправо от плоскости, поэтому поток поля через поверхность куба будет состоять только из потока через две стороны куба, перпендикулярных линиям поля и параллельных плоскости. Теорема Гаусса запишется в виде: 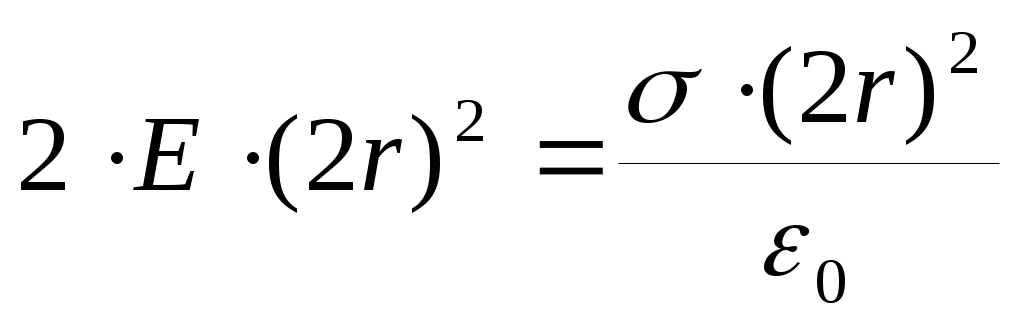 .
.
Таким образом, бесконечная заряженная плоскость создаёт в пространстве однородное поле: 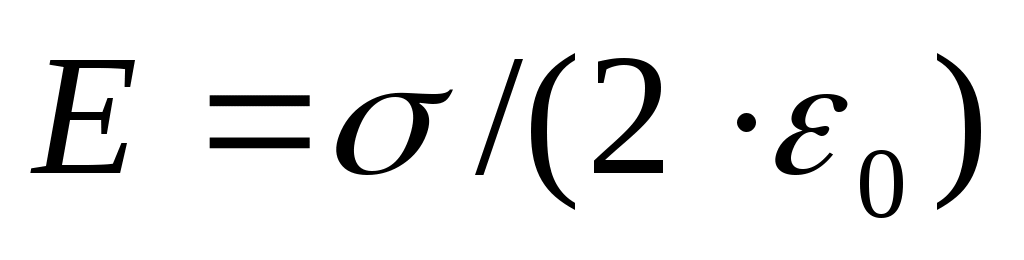 . За нуль потенциала примем потенциал плоскости; тогда потенциал φ=φ2 поля на расстоянии х от плоскости будет:
. За нуль потенциала примем потенциал плоскости; тогда потенциал φ=φ2 поля на расстоянии х от плоскости будет:
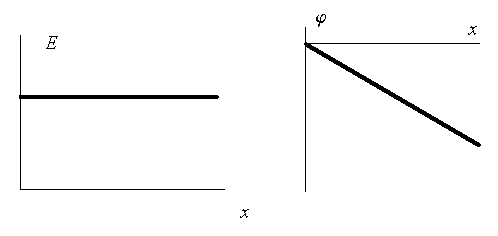
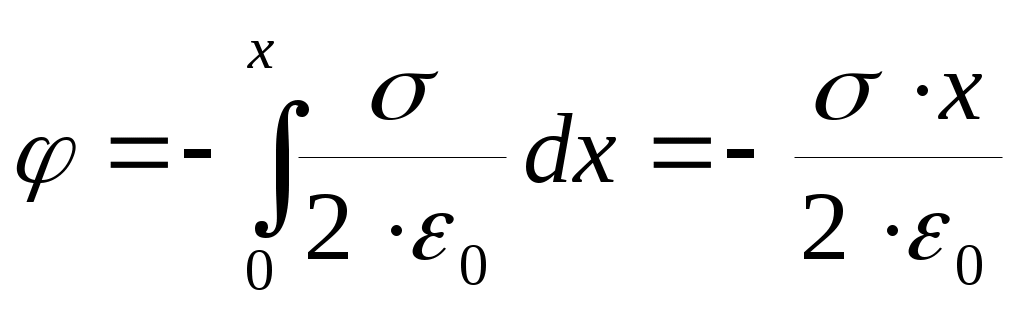 .
.
Графики напряженности и потенциала поля заряженной плоскости:
Расчеты напряженности и потенциала полей, создаваемых заряженными шаром и цилиндром проводятся аналогично.
Конденсатор.
Две бесконечные пластины, заряженные одинаковыми по величине, но разноимёнными зарядами, создают поле, сконденсированное между пластинами; за пластинами поле отсутствует (между пластинами поля от каждой пластины арифметически складываются: E=σ/ε0 , за пластинами – вычитаются E=0).
П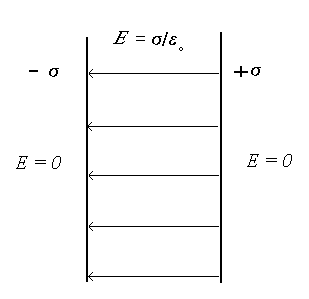 одобные устройства называются конденсаторами электрического поля или просто конденсаторами. Обычно рассматривают плоские, сферические или цилиндрические конденсаторы.
одобные устройства называются конденсаторами электрического поля или просто конденсаторами. Обычно рассматривают плоские, сферические или цилиндрические конденсаторы.
Проводники Проводниками называют вещества, содержащие свободные электрические заряды, то есть такие, которые могут свободно перемещаться по объёму проводника под действием электрического поля. Все металлы являются проводниками.
При помещении незаряженного изолированного проводника во внешнее электрическое поле свободные электрические заряды под действием внешнего поля перемещаются так, что края проводника оказываются заряженными; индуцированные на краях проводника заряды создают собственное поле; разделение зарядов продолжается до тех пор, пока внешнее поле и поле индуцированных зарядов не сравняются по величине; при этом суммарное поле в проводнике исчезнет, движение зарядов прекратится.
Е сли зарядить изолированный проводник, то избыточные электрические заряды отталкиваются и распределятся только на поверхности проводника. Так как внутри проводника нет нескомпенсированных электрических зарядов, то, согласно теореме Гаусса, электрическое поле и внутри заряженного проводника равно нулю. Заряды должны распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовала бы разность потенциалов, что приводило бы к перемещению зарядов, то есть отсутствию равновесия. Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника. Его легко рассчитать по теореме Гаусса:
сли зарядить изолированный проводник, то избыточные электрические заряды отталкиваются и распределятся только на поверхности проводника. Так как внутри проводника нет нескомпенсированных электрических зарядов, то, согласно теореме Гаусса, электрическое поле и внутри заряженного проводника равно нулю. Заряды должны распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовала бы разность потенциалов, что приводило бы к перемещению зарядов, то есть отсутствию равновесия. Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника. Его легко рассчитать по теореме Гаусса: 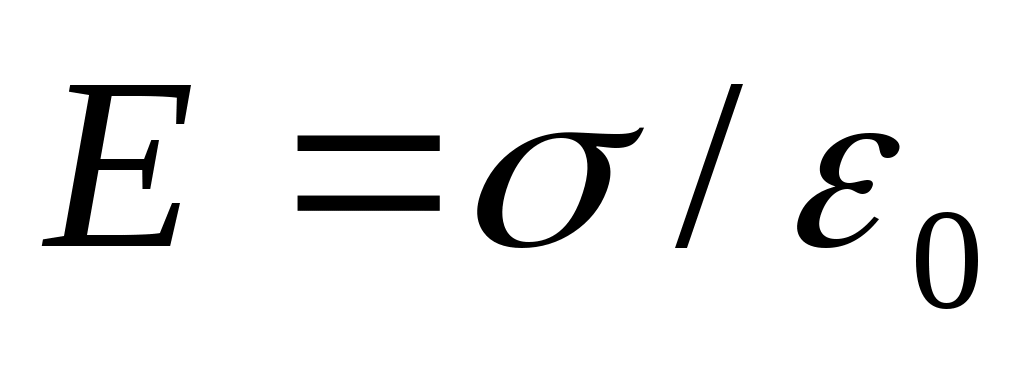 . Это поле не приводит к движению зарядов, ибо заряды не могут покинуть проводник (на поверхности металла существует потенциальный барьер, "запирающий" электроны внутри металла, так называемая "работа выхода электрона из металла").
. Это поле не приводит к движению зарядов, ибо заряды не могут покинуть проводник (на поверхности металла существует потенциальный барьер, "запирающий" электроны внутри металла, так называемая "работа выхода электрона из металла").
2.2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ.
Э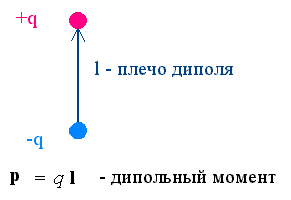
 лектрический диполь. Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент
лектрический диполь. Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент 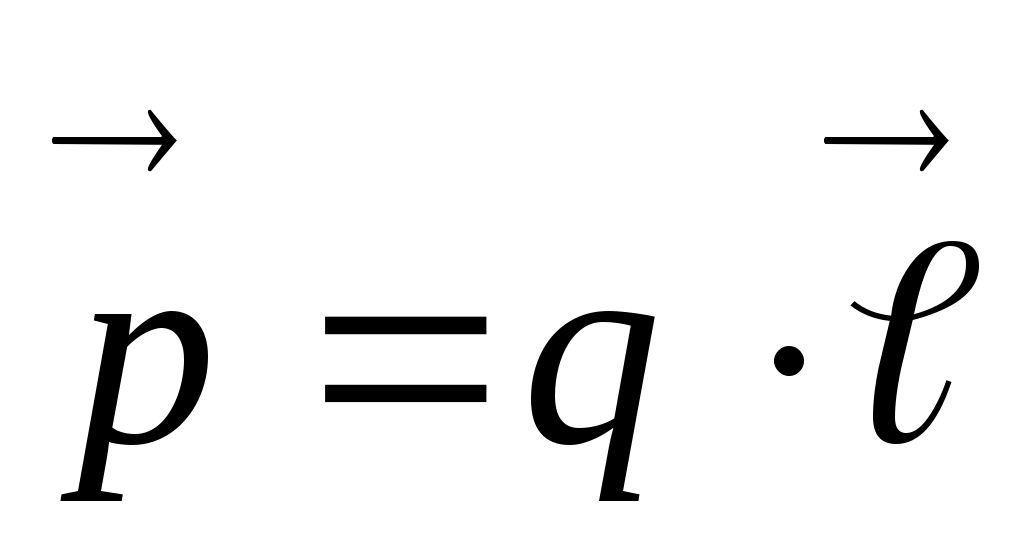 (или электрический момент диполя) - вектор; его направление - от отрицательного заряда к положительному. Электрическое поле
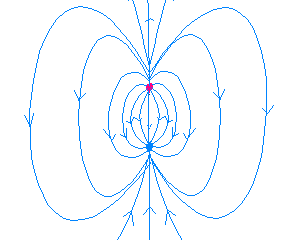
(или электрический момент диполя) - вектор; его направление - от отрицательного заряда к положительному. Электрическое поле 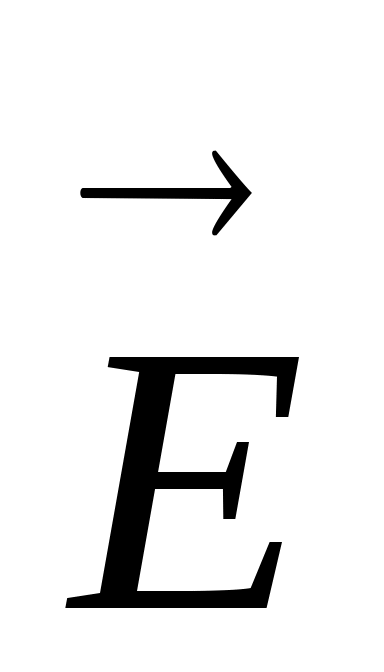 диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно:
диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно: 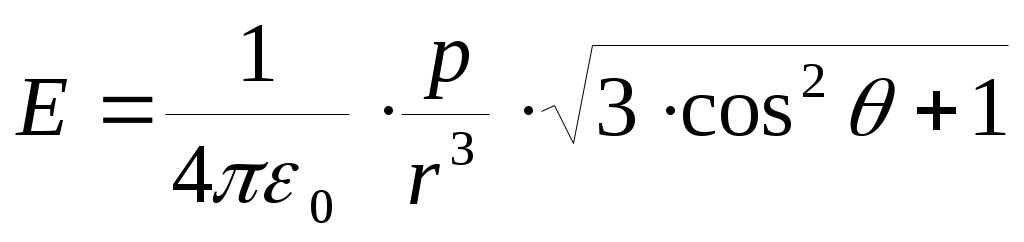 .
.
θ - угол между дипольным моментом и направлением на точку пространства, в которой вычисляется поле. Формула применима для расстояний r >> ℓ. Поле диполя с расстояниемr спадает быстрее (
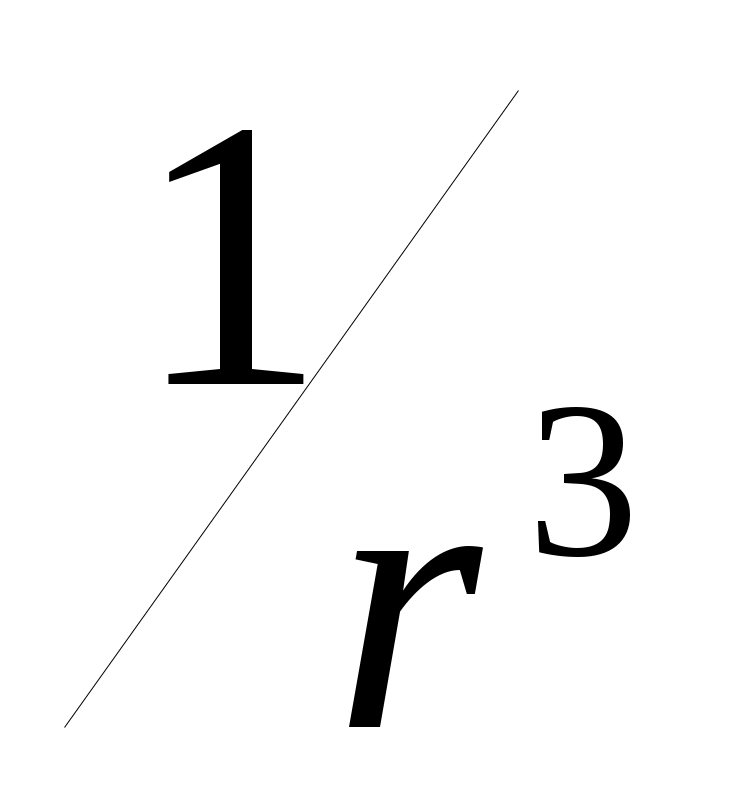 ), чем поле точечного заряда (
), чем поле точечного заряда (
Взаимодействие зарядов. Известно, что одноименные заряды отталкиваются, разноименные - притягиваются. Закон взаимодействия точечных зарядов впервые сформулировал Кулон в 1785 г. (закон Кулона) :
Электрическое поле .
Запишем закон Кулона в виде:
(Поле не просто удобный математический способ описания взаимодействия, а еще одна форма существования материи (наряду с веществом); о его наличии мы судим по силовому воздействию на пробные тела).
Если заряд q взаимодействует с несколькими зарядами, можно сказать, что он взаимодействует с электрическим полем, созданным этими зарядами, при этом электрическое поле вычисляется как векторная сумма полей от каждого заряда (принцип суперпозиции):
Потенциал Электростатическое поле - консервативное силовое поле, то есть работа сил поля A над зарядом q не зависит от траектории движения заряда, а определяется его начальным и конечным положениями. Работу сил такого поля при перемещении заряда q можно представить как разность некоторой функции координат U(r) в начальном и конечном положениях заряда. (Эту функцию координат U(r) называют потенциальной энергией взаимодействия зарядов).
Найдём работу А, совершаемую полем, созданным точечным зарядом Q, при перемещениизаряда q из точки 1 в точку 2:
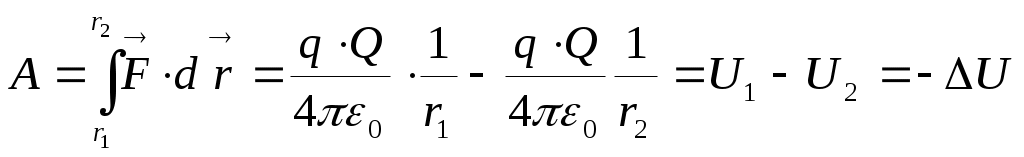 .
.Потенциальной энергией взаимодействия зарядов q и Q будет :
Потенциал φ - это скалярная характеристика электростатического поля, численно равная потенциальной энергии единичного заряда, помещенного в данную точку поля.
В системе единиц СИ напряженность измеряется в Н/Кл=В/м, а потенциал в Дж/Кл=В (Вольт).
Связь напряженности электрического поля и потенциала.
Теорема о циркуляции вектора
И напряжённость и потенциал описывают один объект – электростатическое поле. Найдем связь между ними, исходя из выражения для работы в дифференциальной форме:
Если поделить это выражение на величину пробного заряда q, то получим
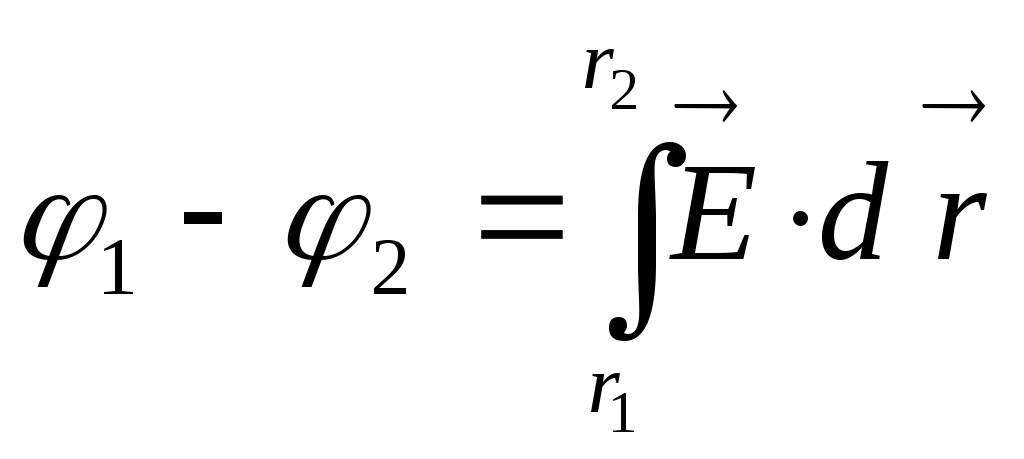 . Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность:
. Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность: Линии поля

Для наглядности принято изображать векторное электрическое поле в пространстве (или на плоскости) с помощью линий электрического поля, которые строятся по следующим правилам: - вектор электрического поля
пространства направлен по касательной к линии поля в этой точке; - направление вектора поля
пространства; - линии поля начинаются на положительных зарядах и кончаются на
отрицательных; либо приходят из бесконечности и уходят в бесконечность; - поскольку в каждой точке пространства поле определено однозначно, линии поля
не могут пересекаться.
Эквипотенциальные поверхности Г
 еометрическое место точек в пространстве, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью (на плоскости - эквипотенциальной линией). Из связи между вектором электрического поля и потенциалом следует, что эквипотенциальные поверхности всегда перпендикулярны линиям электрического поля. Действительно, если две точки на расстоянии dr имеют одинаковые потенциалы (т.е., dφ=0), то из соотношения dφ = - E·dr·cosα = 0, следует, что вектор
еометрическое место точек в пространстве, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью (на плоскости - эквипотенциальной линией). Из связи между вектором электрического поля и потенциалом следует, что эквипотенциальные поверхности всегда перпендикулярны линиям электрического поля. Действительно, если две точки на расстоянии dr имеют одинаковые потенциалы (т.е., dφ=0), то из соотношения dφ = - E·dr·cosα = 0, следует, что векторТеорема Гаусса Потоком напряжённости электрического поля (или просто потоком электрического поля) dФ в вакууме через площадку dS называется величина:
.
Н

апряженность и потенциал поля заряженной плоскости Для вычисления поля, создаваемого бесконечной заряженной плоскостью, воспользуемся теоремой Гаусса, и в качестве гауссовой поверхности выберем куб со стороной 2r. Очевидно, что линии поля направлены перпендикулярно влево и вправо от плоскости, поэтому поток поля через поверхность куба будет состоять только из потока через две стороны куба, перпендикулярных линиям поля и параллельных плоскости. Теорема Гаусса запишется в виде:
Таким образом, бесконечная заряженная плоскость создаёт в пространстве однородное поле:
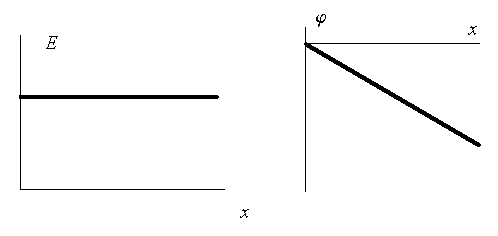
Графики напряженности и потенциала поля заряженной плоскости:
Расчеты напряженности и потенциала полей, создаваемых заряженными шаром и цилиндром проводятся аналогично.
Конденсатор.
Две бесконечные пластины, заряженные одинаковыми по величине, но разноимёнными зарядами, создают поле, сконденсированное между пластинами; за пластинами поле отсутствует (между пластинами поля от каждой пластины арифметически складываются: E=σ/ε0 , за пластинами – вычитаются E=0).
П
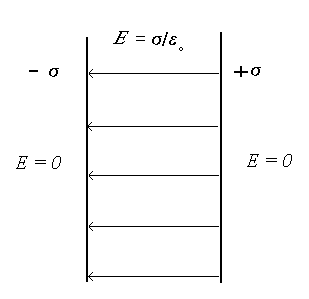 одобные устройства называются конденсаторами электрического поля или просто конденсаторами. Обычно рассматривают плоские, сферические или цилиндрические конденсаторы.
одобные устройства называются конденсаторами электрического поля или просто конденсаторами. Обычно рассматривают плоские, сферические или цилиндрические конденсаторы. Проводники Проводниками называют вещества, содержащие свободные электрические заряды, то есть такие, которые могут свободно перемещаться по объёму проводника под действием электрического поля. Все металлы являются проводниками.
При помещении незаряженного изолированного проводника во внешнее электрическое поле свободные электрические заряды под действием внешнего поля перемещаются так, что края проводника оказываются заряженными; индуцированные на краях проводника заряды создают собственное поле; разделение зарядов продолжается до тех пор, пока внешнее поле и поле индуцированных зарядов не сравняются по величине; при этом суммарное поле в проводнике исчезнет, движение зарядов прекратится.
Е
 сли зарядить изолированный проводник, то избыточные электрические заряды отталкиваются и распределятся только на поверхности проводника. Так как внутри проводника нет нескомпенсированных электрических зарядов, то, согласно теореме Гаусса, электрическое поле и внутри заряженного проводника равно нулю. Заряды должны распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовала бы разность потенциалов, что приводило бы к перемещению зарядов, то есть отсутствию равновесия. Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника. Его легко рассчитать по теореме Гаусса:
сли зарядить изолированный проводник, то избыточные электрические заряды отталкиваются и распределятся только на поверхности проводника. Так как внутри проводника нет нескомпенсированных электрических зарядов, то, согласно теореме Гаусса, электрическое поле и внутри заряженного проводника равно нулю. Заряды должны распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовала бы разность потенциалов, что приводило бы к перемещению зарядов, то есть отсутствию равновесия. Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника. Его легко рассчитать по теореме Гаусса: 2.2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ.
Э

 лектрический диполь. Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент
лектрический диполь. Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга. Дипольный момент θ - угол между дипольным моментом и направлением на точку пространства, в которой вычисляется поле. Формула применима для расстояний r >> ℓ. Поле диполя с расстояниемr спадает быстрее (
) . На продолжении оси диполя (θ=00 или 1800):
Диполь в электрическом поле Н
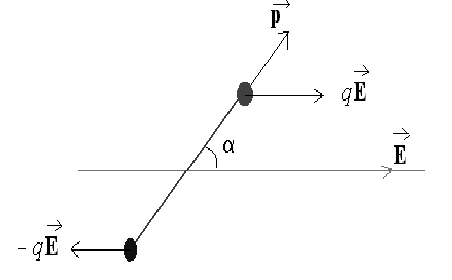 а диполь, находящийся в однородном электрическом поле, действует момент пары сил:
а диполь, находящийся в однородном электрическом поле, действует момент пары сил: Энергия диполя в электрическом поле. Имеется в виду потенциальная энергия диполя в однородном электрическом поле, которая, если диполь "отпустить", произведёт работу, поворачивая диполь. Работа при вращательном движении соответствует убыли потенциальной энергии диполя
Диэлектрики Диэлектрики (или изоляторы) не проводят электрический ток, так как в них, в отличие от проводников, нет свободных зарядов, способных двигаться по объёму диэлектрика под действием электрического поля, а есть только связанные заряды, входящие в состав молекул и перемещающиеся в пределах молекул.
Молекулы диэлектрика бывают двух видов:
– полярные, то есть такие, в которых центры положительных и отрицательных зарядов не совпадают; эти молекулы представляют собой готовые диполи;
– неполярные, то есть не диполи.
Полярные молекулы-диполи во внешнем электрическом поле стремятся выстроиться так, что бы их моменты были направлены вдоль поля. Полного выстраивания не происходит, этому мешает тепловое движение молекул (чем выше поле и ниже температура, тем сильнее выстраивание).
Неполярные молекулы под действием внешнего поля превращаются в диполи, то есть под действием поля положительные и отрицательные заряды в молекулах смещаются в разные стороны; дипольный момент таких молекул всегда направлен вдоль поля. Чем сильнее поле, тем больше дипольный момент; от температуры наведённый таким образом дипольный момент не зависит.
В обоих случаях происходит поляризация диэлектрика – появление результирующего дипольного момента в направлении внешнего поля
Степень поляризации характеризуется вектором поляризации или поляризованностью – дипольным моментом единицы объема диэлектрика:
То есть величина поляризованности просто равна поверхностной плотности наведённых зарядов σ' . Как в случае плоского конденсатора, для поля Е', созданного этими зарядами, можно записать:
Из опыта известно, что поляризованность пропорциональна электрическому полю, ее вызвавшему, т.е.,
Так как
Теорема Гаусса для поля в диэлектрике: Поток вектора
сквозь произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью,:
Ёмкость Разные проводники, несущие одинаковые электрические заряды, в общем случае, имеют разные потенциалы, и, наоборот, проводники с одинаковыми у поверхности потенциалами имеют, в общем случае, разные заряды. Это указывает на то, что они отличаются друг от друга некоторым физическим свойством, которое получило название электрической емкости. Электрической ёмкостью или просто ёмкостью уединенного проводника называется отношение заряда проводника к его потенциалу: C=q / φ. Поскольку потенциал проводника пропорционален его заряду (например, для заряженного шара радиуса R в среде с диэлектрической проницаемостью ε, потенциал у его поверхности