Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 384

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Свободные гармонические незатухающие колебания. Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: (3).Его решением является гармоническая функция: (4), в чем легко убедиться, подставив (4) в (3).В (4) xm , ω0 и φ0 – постоянные величины. xm– амплитуда – величина, указывающая максимальное значе­ние координаты х при отклонении от положения равновесия, ω0 – собственная частота, аргумент косинуса носит название фазы колебания; φ0 — начальная фаза коле­бания (в момент t= 0). Частота колебаний зависит только от свойств колеблю­щейся системы, но не от амплитуды, а амплиту­да и начальная фаза колебаний определяются начальными условиями ее движения, выводя­щими систему из состояния покоя.Скорость колеблющейся частицы равна: (5). Ускорение частицы при таком движении: (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0=0.Складывая кинети­ческую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы: (7).Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потен­циальная энергии изменяются со временем, как sin2(ω0·t+φ0) и cos2(ω0·t+φ0) , так что когда одна из них увеличивает­ся, другая – уменьшается, т.е. процесс колеба­ний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Сред­ние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения час­тицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x , действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса).Примечание: В механике обычно рассматривают колебания : – математического маятника с периодом , где ℓ–длина маятника;– физического маятника с периодом , где J–момент инерции маятника, a–расстояние от точки подвеса маятника до его центра масс;– пружинного маятника с периодом , где k–жесткость пружины.2. Свободные затухающие колебанияПри наличии силы трения (r ≠0) и отсутствии внешней периодической силы (F0 =0) уравнение движения имеет вид: (8),г де β называется коэффициентом затухания колебаний. В случае слабого затухания (β – мало) решением такого дифференциального уравнения является функция : (9). В этом можно убедиться прямой подстановкой (9) в уравнение (8). – частота колебаний системы с затуханием. A=A0·e-βt – амплитуда затухающих колебаний.Таким образом, амплитуда колебаний убыва­ет по экспоненциальному закону. Вместе с амплитудой убывает также и энергия колебаний W, т.к. WA2.Степень убывания амплитуды определяется коэффициен­том затухания β. Время τ=1/β, за которое амплитуда колебаний уменьшается в е=2.7183 раз, называют по­стоянной времени затухания колебаний.Скорость уменьшения амплитуды за период характеризует величина θ, называемая лога­рифмическим декрементом затухания. По определению: (10).Скорость убывания энергии в системе с зату­ханием характеризует добротность Q: (11),где W – энергия, запасенная в системе, (–ΔW)– энергия, теряемая системой за период. Добротность показывает, во сколько раз энер­гия, запасенная в системе, больше энергии, те­ряемой за период. Добротность в (11) выражена через параметры системы и логарифмический декремент затухания θ, с учетом того, что W

1.10. ОСНОВЫ ТЕРМОДИНАМИКИТермодинамика– учение о превращениях одного вида энер­гии в другой, о передаче энергии от тела к телу. Термодинамика изучает свойства макроскопических тел без рассмотрения их молекулярной структуры. Термодинамическая система (ТС) –макроскопические тела, которые могут обмениваться энергией как друг с другом, так и с внешней средой.Равновесное состояние ТС - состояние, при котором термодинамические параметры (давление, температура и объем) остаются постоянными сколь угодно долго при неизменных внешних условиях. Термодинамический процесс – изменение состояния ТС, характеризующееся изменением ее параметров. Состояние ТС характеризуют также внутренней энергией, которая равна сумме кинетических энергий беспорядочного движения всех молекул и потенциальных энергий взаимодействия молекул друг с другом. Система тел называется изолированной, или замкнутой, если нет обмена энергией с окружающей средой. Первое начало термодинамикиТела и системы могут обмениваться энергией друг с другом. Существует два вида обмена энергией. Это может быть работа, произведенная одним телом (системой) над другим телом (сис­темой). Примером мо­жет служить перемещение тела или его частей под действием упругих, электрических или других сил.Другой способ обмена энергией – путем передачи энергии неупорядоченного, хаотического движения молекул. Тогда гово­рят о передаче тепла. Например, передача энергии от нагретого тела к холодному происходит за счет передачи кинетической энергии хаотически движущихся молекул одного тела хаотичес­кому движению молекул другого тела. В обоих этих случаях изменяется внутренняя энергия U.Сказанное выше можно записать как: ΔU = Q+А’, где Q – энергия,поступающая в систему при теплообмене, а А’– работа, совершаемая внешнимителами над системой. Исторически принято это соотношение записывать как: Q = ΔU + А (18), где А = – А’ –работа, совершаемая самой системой.(18), представляющее собой закон сохранения энер­гии, получило название первого начала термодинамики: «Подведенное к телу количе­ство теплоты идет на увеличение внутренней энергии тела и на работу, которую тело производит». Очень важно отметить различие между величинами U с одной стороны, и А и Q – с другой. Внутренняя энергия U– это функция состояния системы. Если в состоянии 1 внутренняя энергия равна U1 , то что бы ни происходило с системой, какую бы работу она ни соверша­ла, какие бы количества теплоты к ней ни подводились, если систе­ма вернулась в то же состояние 1 (т. е. процесс оказался круговым, совершен цикл), ее внутренняя энергия будет снова U1 (ΔU=0).В то же время Q и А – это только передаваемые телу или получаемые от тела порции энергии. Они связаны с передачей энергии, а не с каким-то запасом их в теле. Бессмысленно гово­рить о запасе работы в теле. И так же бессмысленно говорить о запасе теплоты в теле. Работа и теплота не являются функция­ми состояния тела. Переходя к бесконечно малым порциям энергии, запишем первое начало в дифференциальной форме: δQ = dU + δA. (19).Здесь специально даны разные обозначения бесконечно малых («d...» и «δ…»), чтобы отразить то обстоятельство, что U – функ­ция состояния, a Qи А – нет. Работа расширения идеального газа при различных процессах На рисунке а приведена зависимость давления газа от его объема. Точка 1 означает состояниегаза, так как указывает его дав­ление и объем в данный момент. Температуру при этом можно найти из (4). Линии означают процессы, так как показывают, через ка­кие состояния система проходит. Процесс может быть без изменения давления (прямая I на рисунке а). Такой процесс называется изобарическим. Изохорическийпроцесс (прямая II) – это процесс без изменения объе­ма. Процесс без изменения температуры (изотермический)будет примерно та­ким, как показано кривой III. Это гипербола, так как при Т = const давление обратно пропорционально объему: p

Взаимодействие зарядов. Известно, что одноименные заряды отталкиваются, разноименные - притягиваются. Закон взаимодействия точечных зарядов впервые сформулировал Кулон в 1785 г. (закон Кулона) : , где q, Q - взаимодействующие заряды,  -единичный вектор в направлении радиус-вектора , r - расстояние между зарядами; сила направлена вдоль прямой, соединяющей заряды. ε0 = 8.85·10-12 Ф/м – электрическая постоянная.Электрическое поле .      Запишем закон Кулона в виде:       .   Теперь его можно прочитать так: сила взаимодействия двух зарядов равна произведению первого заряда q на нечто, что зависит только от второго заряда Q и от расстояния до него.  Это нечто и называется электрическим полем заряда Qили - более строго - напряжённостью электрического поля, создаваемого зарядом Q. Напряженность– векторная характеристика электрического поля, численно равная силе, с которой поле действует на единичный электрический заряд, помещенный в рассматриваемую точку поля: .(Поле не просто удобный математический способ описания взаимодействия, а еще одна форма существования материи (наряду с веществом); о его наличии мы судим по силовому воздействию на пробные тела). Если заряд q взаимодействует с несколькими зарядами, можно сказать, что он взаимодействует с электрическим полем, созданным этими зарядами, при этом электрическое поле вычисляется как векторная сумма полей от каждого заряда (принцип суперпозиции): .Потенциал              Электростатическое поле - консервативное силовое поле, то есть работа сил поля A над зарядом q не зависит от траектории движения заряда, а определяется его начальным и конечным положениями. Работу сил такого поля при перемещении заряда q можно представить как разность некоторой функции координат U(r) в начальном и конечном положениях заряда. (Эту функцию координат U(r) называют потенциальной энергией взаимодействия зарядов). Найдём работу А, совершаемую полем, созданным точечным зарядом Q, при перемещениизаряда q из точки 1 в точку 2: .Потенциальной энергией взаимодействия зарядов q и Q будет : , где величина – называется потенциалом точечного заряда  Q в точке  пространства на расстоянии r от него.Потенциал φ - это скалярная характеристика электростатического поля, численно равная потенциальной энергии единичного заряда, помещенного в данную точку поля.В системе единиц СИ напряженность измеряется в Н/Кл=В/м, а потенциал в Дж/Кл=В (Вольт).Связь напряженности электрического поля и потенциала. Теорема о циркуляции вектора .        И напряжённость и потенциал описывают один объект – электростатическое поле.  Найдем связь между ними, исходя из выражения для работы в дифференциальной форме: .Если поделить это выражение на величину пробного заряда q, то получим или или для одномерного случая. В общем виде это выражение записывается как: (произносится так: «напряженность поля равна со знаком минус градиенту потенциала φ») , где . Можно также вычислить разность потенциалов двух точек поля: . Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность: . Если единичный заряд возвращается в начальную точку, то работа электростатических сил по замкнутому контуру равна нулю: . Это соотношение носит название теоремы о циркуляции, а сам интеграл называется циркуляцией вектора по замкнутому контуру ℓ.Линии поля Для наглядности принято изображать векторное электрическое поле в пространстве (или на плоскости) с помощью линий электрического поля, которые строятся по следующим правилам: - вектор электрического поля в каждой точкепространства направлен по касательной к линии поля в этой точке; - направление вектора поля совпадает с направлением линии поля; - густота линий поля отражает величину вектора поля в данной области пространства; - линии поля начинаются на положительных зарядах и кончаются наотрицательных; либо приходят из бесконечности и уходят в бесконечность; - поскольку в каждой точке пространства поле определено однозначно, линии поляне могут пересекаться. Эквипотенциальные поверхности Г еометрическое место точек в пространстве, имеющих одинаковый потенциал, называется эквипотенциальной поверхностью (на плоскости - эквипотенциальной линией).  Из связи между вектором электрического поля и потенциалом следует, что эквипотенциальные поверхности всегда перпендикулярны линиям электрического поля. Действительно, если две точки на расстоянии dr имеют одинаковые потенциалы (т.е., dφ=0), то из соотношения dφ = - E·dr·cosα = 0, следует, что вектор и вектор , соединяющий две точки на эквипотенциали, взаимно перпендикулярны (α=900). Если между соседними поверхностями одинаковая разность потенциалов, то густота эквипотенциалей, как и густота линий поля, будет отражать величину электрического поля в пространстве.Теорема Гаусса Потоком напряжённости электрического поля (или просто потоком электрического поля) dФ в вакууме через площадку dS называется величина: . Вектор площади направлен по нормали к её поверхности, а его модуль равен площади площадки dS. (У площадки две стороны, поэтому всегда надо оговаривать, какую нормаль принимать за положительную) . Рассчитаем поток вектора через сферическую поверхность радиусаr для поля, создаваемого точечным зарядом q, находящимся внутри этой поверхности : . Этот результат оказывается справедливым для замкнутой поверхности произвольной формы и для любого количества зарядов внутри такой поверхности и получил название теоремы Гаусса для электростатического поля в вакууме. Теорема Гаусса: поток вектора напряжённости электростатического поля сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов , охватываемых поверхностью S, деленной на электрическую постоянную ε0: ..Н апряженность и потенциал поля заряженной плоскости Для вычисления поля, создаваемого бесконечной заряженной плоскостью, воспользуемся теоремой Гаусса, и в качестве гауссовой поверхности выберем куб со стороной 2r. Очевидно, что линии поля направлены перпендикулярно влево и вправо от плоскости, поэтому поток поля через поверхность куба будет состоять только из потока через две стороны куба, перпендикулярных линиям поля и параллельных плоскости. Теорема Гаусса запишется в виде: .Таким образом, бесконечная заряженная плоскость создаёт в пространстве однородное поле: . За нуль потенциала примем потенциал плоскости; тогда потенциал φ=φ2 поля на расстоянии х от плоскости будет: .Графики напряженности и потенциала поля заряженной плоскости: Расчеты напряженности и потенциала полей, создаваемых заряженными шаром и цилиндром проводятся аналогично. Конденсатор.         Две бесконечные пластины, заряженные одинаковыми по величине, но разноимёнными зарядами, создают поле, сконденсированное между пластинами; за пластинами поле отсутствует (между пластинами поля от каждой пластины арифметически складываются: E=σ/ε0 , за пластинами – вычитаются E=0). П одобные устройства называются конденсаторами электрического поля или просто конденсаторами. Обычно рассматривают плоские, сферические или цилиндрические конденсаторы. Проводники Проводниками называют вещества, содержащие свободные электрические заряды, то есть такие, которые могут свободно перемещаться по объёму проводника под действием электрического поля. Все металлы являются проводниками.При помещении незаряженного изолированного проводника во внешнее электрическое поле свободные электрические заряды под действием внешнего поля перемещаются так, что края проводника оказываются заряженными; индуцированные на краях проводника заряды создают собственное поле; разделение зарядов продолжается до тех пор, пока внешнее поле и поле индуцированных зарядов не сравняются по величине; при этом суммарное поле в проводнике исчезнет, движение зарядов прекратится.Е сли зарядить изолированный проводник, то избыточные электрические заряды отталкиваются и распределятся только на поверхности проводника. Так как внутри проводника нет нескомпенсированных электрических зарядов, то, согласно теореме Гаусса, электрическое поле и внутри заряженного проводника равно нулю. Заряды должны распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовала бы разность потенциалов, что приводило бы к перемещению зарядов, то есть отсутствию равновесия. Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника.  Его легко рассчитать по теореме Гаусса: . Это поле не приводит к движению зарядов, ибо заряды не могут покинуть проводник (на поверхности металла существует потенциальный барьер, "запирающий" электроны внутри металла, так называемая "работа выхода электрона из металла").2.2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ.Э лектрический диполь. Диполем называется система из двух одинаковых по величине, но разных по знаку электрических зарядов q, находящихся на расстоянии ℓ друг от друга.  Дипольный момент (или электрический момент диполя) - вектор; его направление - от отрицательного заряда к положительному. Электрическое поле диполя в каждой точке пространства определяется суперпозицией полей двух точечных зарядов, схематично представлено на рисунке и равно: .θ - угол между дипольным моментом и направлением на точку пространства, в которой вычисляется поле. Формула применима для расстояний r >> ℓ.  Поле диполя с расстояниемr спадает быстрее ( ), чем поле точечного заряда (

Электромагнитная индукция. Правило Ленца Опыт показывает, что если в катуш­ку, соединенную с гальванометром, вдви­гать постоянный магнит (рис. а), то гальванометр покажет ток тогда, когда магнит движется. Если магнит, наоборот, удалять из ка­тушки, то в ней идет ток обратного направления.Это явление, открытое Фарадеем, называет­ся электромагнитной индукцией, возникающий ток называется индукционным током, а распре­деленная по катушке э.д.с., под действием кото­рой течет ток, называется э.д.с. индукции. Причем э.д.с. индукции возникает в контуре всегда, а ток – только, если контур замкнут и яв­ляется проводником. Существенно именно не движение магнита, а изменение магнитного потокаФ через катушку. Например, в опыте, изображенном на верхнем рис., во внутреннем контуре возникает индукционный ток, если во внешнем с помощью реостата менять силу тока, получае­мого от внешнего источника. Причем, если во внешнем кон­туре ток увеличивать, так что поток Ф, создаваемый этим током, растет, то вовнутреннем контуре возникает индукционный ток противоположного направления. Он своим магнитным потоком Фi будет препятствовать нарастанию потока Ф. Если же силу тока в одном из конту­ров и, следовательно, поток Ф, уменьшать, например, разомкнув цепь внутреннего контура на нижнем рис., то в другом контуре возникнет индукционный ток и маг­нитный поток Фi того же направления, чтобы препятствовать уменьшению потока Ф.Ленц сформулировал это следующим образом (правило Лен­ца): индукционный ток возникает такого направления, что он своим магнитным действием препятствует той причи­не, в результате которой он возник.Формула Фарадея для э.д.с. индукцииИ спользуя закон сохранения энергии, получим формулу для э.д.с. индукции. Рассмотрим схему на рис. Перемычку будем сами двигать влево. При этом поток Ф, пронизывающий кон­тур, будет уменьшаться на dΦ. Возникает индукционный ток Iтакого направления, что действующая на него сила Ампера FA согласно правилу Ленца препятствует движению.Будет совершена работа по передвижению провода с током в магнитном поле: dA = –I·dΦ. Знак «–» поставлен потому, что работу совершают сторонние силы, а не силы поля. Эта работа приводит к возникновению э.д.с. индукции εинд, индукционного тока и к выделению тепловой энергии в цепи: dA = I· εинд·dt. Приравнивая выражения для работ, получим формулу Фарадея для э.д.с. индукции: εинд=–dΦ/dt . Эта э.д.с. является результатом действия сторонних сил и может быть записана в виде: .В это выражение не входят величи­ны, отражающие какие-либо свойства материа­ла, из которого сделан контур. Следовательно, э.д.с. электромагнитной индукции от этих свойств не зависит. Это позволяет считать, что измене­ние магнитного поля вызывает появление элект­рического поля. Ток, протекающий в контуре, является следствием электрического поля.Если контур состоит из N витков, то индуцируе­мая в контуре э.д.с. будет равна сумме э.д.с. , инду­цируемых в каждом из витков в отдельности: .Величина называется потокосцеплением, или полным магнитным потоком. Если по­ток, пронизывающий каждый из витков, одина­ков, то Ψ=N·Φ.Приведем выражения для э.д.с. индукции при различных способах ее возбуждения:− э.д.с. индукции, возникающая в проводнике длиной ℓ, движу­щемся под углом α к силовым линиям со скоростью υ: ; − э.д.с. индукции, возникающая в контуре , вращающемся в магнитном поле: ;− э.д.с. индукции, возникающая в контуре при изменении его площади: ;− э.д.с. индукции, возникающая в контуре, помещенном в изменяющееся магнитное поле: . Самоиндукция Э.д.с. индукции может возникать и в самом контуре с меняющимся токомI. Другого контура при этом может и не быть. При усилении тока (и следовательно, увеличении потока Ф) в контуре воз­никает э.д.с. индукции и индукционный ток Iинд такого направления, чтобы препятствовать усилению тока I. Это явление носит на­звание самоиндукции. Так как магнитный поток Ф, пронизывающий контур, пропорционален силе тока: Ф = L·I , то э.д.с. самоиндукции пропорциональна скорости изменения тока: , где L – коэффициент самоиндукции или индуктивностька­тушки.Найдем индуктивность длинного со­леноида. Поток Ф через один виток равен B·S. Через все N витков соленоида Ψ = N·B·S. Индукция в соленоиде равна B=μ0·(N/ℓ)·I. Так что .Сравнивая два выражения, найдем: , где V=S·ℓ–объем внутри соленоида, ℓ– длина соленоида, n–число витков на единице длины соленоида (густота намотки). Т.о., индуктивность соленоида очень сильно зависит от густоты намотки n. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ Магнетики. Напряженность магнитного поля.Все вещества являются магнетиками, т.е. при помещении их во внешнее магнит­ное поле изменяют свое состояние – намаг­ничиваются. Находясь во внешнем магнитном поле, намагниченные вещества сами становят­ся источниками поля . Собственное магнитное поле , накладываясь на магнитное поле , в сумме дает .Вещества, в которых поля и направлены одинаково, называют парамагнетиками. Ве­щества, в которых поля и направлены в противоположные стороны, называют диамагнетиками.Степень намагничивания вещества характе­ризуется вектором намагниченности . Это вектор, среднее значение которого равно отно­шению суммарного магнитного момента всех частиц, расположенных в объеме магнетика, к этому объему: , где ΔV– физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, – магнитный момент отдельной мо­лекулы. Суммирование производится по всем молекулам, заключенным в объеме ΔV. Единицей намагниченности является ампер на метр(А/м). Линии вектора и при наличии вещества остаются всюду замкнутыми. Для описания поля , создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины ℓ, внесенного в однородное внешнее магнитное поле с индукцией .В озникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору . Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис.). Некомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.Ток, текущий по боковой поверхности цилиндра I’, подобен току в соленоиде и создает внутри него поле, магнитнуюиндукцию В’ которого можно вычислить, учитывая формулу для соленоида из одного витка: B’=μ0·I’/ℓ,где I’–сила молекулярных токов (т.н. ток намагничи-вания), ℓ – длина рассматриваемого цилиндра. Магнитный момент этого тока P = I’·S= I’·S·ℓ/ℓ = I’·V /ℓ, где S и V — площадь сеченияи объем магнетика, соответственно. Если Р – суммарный магнитный момент магнетика объемом V, то намагниченность магнетика: J=P/V=I’/ℓ. Т.о., получим связь между B’ и J: . Теорему о циркуляции вектора для вещества можно представить в виде: . Если в этом выражении сделать замену: I’= J·ℓ , то получим или, вводя вспомогательный вектор , получивший название напряженности магнитного поля,: . Это выражение очень удобно, так как в правой части не содержит микро- (молекулярные) токиI’, которые очень трудно оценить, и представляет собой теорему о циркуляции вектора : циркуляция вектора напря­женности магнитного поля по произвольному контуру равна алгебраической сумме макроско­пических токов, охватываемых этим контуром.Вектор намагниченности принято связывать не с магнитной индукцией , а с напряженностью поля : , где безразмерная величина χ называется магнитной восприимчи­востью. Для диамагнетиков χ − отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков χ − положительна (поле молекулярных токов совпадает с внешним).В диа- и парамагнетиках при не очень сильных полях χне зависит от Н и: ,где безразмерная величина μ=1+χ называется магнитной проницаемостью вещества. μ и χ характеризуют магнитные свойства магнетиков.Так как абсолютное значение магнитной восприимчивости χ для диа- и парамагнетиков очень мало (порядка 10–4−10–6), то μ для них незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков μ < 1, для парамагнетиков μ > 1, причем как у тех, так и у других μотличается от единицы весьма мало, т.е. магнитные свойства этих магнетиков выражены очень слабо.Природа магнетизма. Ферромагнетики. Причина усиления в парамагнетиках состоит в том, что ато­мы или молекулы вещества представляют собой магнитные дипо­ли (обладают магнитными моментами). Эти диполи ориентируются во внешнем поле вдоль силовых линий и усиливают его. Если в соленоид вставлен сердечник из пара­магнетика, то дипольные моменты ато­мов (на рис. – стрелки) ориентируются вдоль по полю. В парамагнетике этот эффект очень слаб, и μ близко к единице, так как из-за теплового движения происходит только незначительная преимущественная ориентация диполей вдоль поля (рис.а). В молекулах диамагнетиков магнитный момент отсутствует, но он появляется при помещении диамагнетика во внешнее магнитное поле. Результирующий магнитный момент в диамагнетике мал, всегда направлен против внешнего поля и от температуры не зависит.С уществуют вещества, в которых μ

2.8. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ. Если электрические и магнитные поля изме­няются во времени, то по отдельности их рас­сматривать уже нельзя: взаимное превраще­ние электрических и магнитных полей приводит к появлению электромагнитной волны.Для среды – однородного и изотропного диэлектрика, не обладающего сегнетоэлектрическими или ферромагнитными свойствами, из уравнений Максвелла можно получить, что векторы напряженностей переменного электромагнитного поля удовлетворяют уравнениям: и , где - оператор Лапласа. Но это уравнения, описывающие волновой процесс, в которых скорость распространения волны определяется коэффициентом, стоящим перед второй производной по времени: Решением этих уравнений является т.н. плоская монохроматическая гармоническая волна: , , где - волновой вектор, указывающий направление распространения волны. Т.о., переменное электромагнитное поле действительно распространяется в пространстве в виде волн. Если волна распространяется в вакууме ( ), то . Этот результат в точности совпадает с изме­ренным значением скорости света с, что послу­жило основой для создания электромагнитной теории света. Свойства электромагнитных волн– Электромагнитные волны – поперечные волны; векторы и лежат в плоскости, перпендикулярной к скорости волны в данной точке поля.– Векторы и взаимно перпендикулярны и образуют с направлением распространения волны, т.е. скоростью , правовинтовую систему (рис.).– Взаимно перпендикулярные векторы и колеблются в одной фазе, причем мгновенные значения EиH связаны соотношением: , т.е. они д остигают максимума и обра­щаются в нуль в одних и тех же точках в одни и те же моменты времени. – В вакууме скорость электромагнитной волны равна с и не зависит от частоты.– Объемная плотность энергии электромаг­нитного поля складывается из объемных плотностей энергии электрического и магнитного полей: . С учетом соотношения, связывающего E и H, получим: .– Направление распространения электромаг­нитной волны и энергию, переносимую волной в единицу времени через перпен­дикулярно ориентированную площадку единичной площади, опреде­ляет вектор Умова—Пойнтинга, аналогичный вектору Умова, введенному для механической волны,: . Среднее значение модуля этого вектора представляет интенсивность волны.– Поскольку различные электромагнитные вол­ны имеют общую природу, их можно представить в виде единой шкалы.Вся шкала условно подразделена на 6 диа­пазонов в порядке уменьшения длины волны (возрастания частоты) : радиоволны (длинные, средние и короткие) (от нескольких км до 0,1 мм); инфракрасное излучение (от 0, 1 мм до 0,74 мкм); видимое излучение (от 0,74 до 0,38 мкм); ультрафиолетовое излучение ( от 0,38 мкм до 1нм (10 - 9м )); рентгеновское излучение ( от 1 нм=10 Å до 0,1 Å (1Å=10 -10м )); гамма-излучение ( короче, чем 0,1Å). Радиоволны обусловлены переменными то­ками в проводниках и электронными потоками. В инфракрасной, видимой и ультрафиолетовой областях излучают атомы, молекулы и быстрые заряженные частицы. Рентгеновское излучение возникает при внутриатомных процессах, γ-излучение имеет ядерное происхождение. Частич­но диапазоны перекрываются, т.к. волны одной и той же длины могут излучаться в разных про­цессах. ФИЗИКА. Часть 3. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ СВЕТА . Интерференция света Пусть в произвольную точку наблюдения Р на экране Э приходят две волны (рис.): и , где ЕI и ЕII – напря­женности электри­ческих полей световых волн, идущих от источников S1 и S2 , ω1 и ω2 – частоты волн, -соответствующие волновые векторы. Сложение таких колебаний (можно применить формулу косинусов) дает: .Если учесть, что интенсивность волны пропорциональна квадрату амплитуды (I

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля. Дифракция – явление отклонения света от прямолинейного распространения в неоднородной среде, при котором свет, огибая препятствия, заходит в область геометрической тени, – возни­кает, когда свет падает на препятствия, размеры которых сравнимы с длиной световой волны.По принципу Гюйгенса, каждую точку фрон­та волны можно рассматривать как самостоя­тельный источник вторичных сферических волн. По Френелю, волновое возмущение в любой точке пространства – результат интерферен­ции этих вторичных когерентных волн. Различают т.н. дифракцию Френеля или сферических волн и дифракцию Фраунгофера или плоских волн.Метод зон Френеля. Волновую поверхность разбивают на зоны так, чтобы расстояния от краев соседних зон до точки наблюдения Pотличались на λ/2 (рис.). В этом случае фазы приходящих от соседних зон колеба­ний отличаются на π , сами колебания противоположны по фазе, поэтому при наложении волн они взаимно ослабляют друг друга. Тогда амплиту­да Eрезультирующих колебаний может быть представлена в виде знакопеременного ряда: Дифракция Френеля на круглом отверстии. Пусть в отверстии помещается m зон. Так как амплитуды сферических волн убывают с увеличением расстояния до т.Р, то приближенно выполняется равенство: Ek=(Ek-1+Ek+1)/2 , т.е. амплитуда волны от k-зоны равна среднему арифметическому амплитуд волн от примыкающих к ней зон. Тогда все выражения в круглых скобках обращаются в нуль и для результирующей амплитуды колебаний в т.Р получим: , где: знак «+» соответствует нечетному числу m зон , открываемых отверстием (например, для m = 5 и наблюдается максимум – светлое пятно); знак «–» соответствует четному числу m зон , открываемых отверстием (например, для m = 4 и наблюдается минимум – темное пятно). Если отверстие будет большим (или экрана вообще не будет), то поместятся много зон и в результате . Это означает, что в т.Р попадает свет только от первой зоны, и таким образом объясняется прямолинейное распространение света. Е сли на место Рпоместить экран, то вокруг точки Р будут минимумы и макси­мумы освещенности, имеющие форму колец.. В центре, т. е. в точке Р, может быть как свет, так и темнота, в зависимости от числа зон Френеля, уместившихся в отверстии. Эти теоретические рас­суждения прекрасно подтвердились на опыте.Но самый поразительный результат был получен при рассмот­рении дифракции на круглом непрозрачном экране(рис.). В этом случае несколько центральных зон (например, m) закрыва­ются, а все остальные зоны открыты. Это значит, что в центре тени от малого предмета всегда должно быть свет­лое пятнышко (рис.) . Оно получило название пятна Пу­ассона. На опыте это подтвердилось, что стало блестящим доказательством волновой природы света.Дифракция Фраунгофера на щелиП лоская электромагнитная волна падает нор­мально на преграду со щелью ширины b. Если бы не было дифракции, световые лучи, пройдя через щель, сфокусировались бы в точ­ке F, лежащей на главной оптической оси линзы (рис.). Однако, наблюдаемое на экране распределение интенсивности света имеет в центре резкий максимум освещенности, относительно которого симметрично располагаются чередуясь светлые и темные полосы. Наблюдаемую дифракционную картину можно объяснить с по­мощью построения зон Френеля. Разобьем открытую часть волновой поверх­ности на N элементарных зон ширины b/N. Каж­дая зона создает вторичные волны одинаковой амплитуды E0 / N. Если откры­тая часть волновой поверхности разбивается из точки наблюдения Р на четное число зон, то бу­дет минимум интенсивности, т.к. колебания от каждой пары соседних зон приходят в противофазе и взаимно гасят друг друга. Наоборот, если число зон будет нечетным, то результирующая интенсивность в точке наблю­дения будет максимальной, т.к. действие одной из зон окажется нескомпенсированным. Т.о., условие дифракционного минимума: b·sinφ=m·λ. Условие дифракционного максимума: b·sinφ=(2·m+1)λ/2. Дифракция Фраунгофера на дифракционной решеткеДифракционная решетка – это система из большого числа N параллель­ных друг другу щелей шириной b. Щели разделе­ны непрозрачными, равными по ширине, про­межутками а. Расстояние d = а + bназывается периодом решетки.Пусть плоская монохроматическая световая волна интенсивности I0 падает на решетку нор­мально. Колебания, исходящие от щелей, коге­рентны, они интерферируют друг с другом, и дифракционная картина состоит из достаточно узких интенсивных максимумов.В центр дифракционной картины (φ = 0) коге­рентные колебания от всех щелей приходят в фазе, поэтому наблюдается центральный максимум освещенности.Аналогичный резуль­тат получается и при углах дифракции φ, для кото­рых оптическая разность хода Δ колебаний от со­седних щелей равна целому числу длин волн:Δ=d·sinφ=m·λ. (m=0,1,2…) В направлениях φ, определяемых этим уравне­нием, возникают максимумы. Их называют глав­ными максимумами m-го порядка, а само урав­нение – у словием главных максимумов (рис. ).Из этой формулы следует, что лучи различной длины волны будут иметь максимумы в различ­ных направлениях. Если на дифракционную ре­шетку падает белый свет, то центральный мак­симум (φ = 0) будет представлять собой белую полосу. Во всех остальных порядках будет наблюдаться радужное цветовое размытие (сплошной спектр), обращенное к централь­ной белой полосе фиолетовым краем.С увеличением числа щелей растут интенсив­ность и резкость главных максимумов. Положение минимумов освещенности для дифракционной решетки определяется также, как и для одной щели: b·sinφ= m'·λ., где m' = 1,2,3... Разрешающая способность решетки по­казывает ее способность различать две очень близко расположенные линии в спектре и определяется формулой R=λ/Δλ,где Δλ – наименьшая разность длин волн двух соседних спектральных линий λ и λ+Δλ, при которой эти линии в спектре видны раздельно.Угловая дисперсия D определяет угловую ширину спектра D = dφ/dλ. Она численно равна угловому расстоянию dφ между двумя линиями спектра, длины волн которых различаются на единицу. Дифракция рентгеновских лучей. Для рентгеновских лучей в качестве дифракционной решетки можно использовать кристаллы, в которых расстояние между атомными плоскостями d сравнимо с длиной волны λ(λ

Формула Планка для испускательной способности АЧТ: точно согласуется с данными опытов и объясняет все экспериментальные законы теплового излучения тел. 3.4. ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА. ДАВЛЕНИЕ СВЕТА. Фотоэффект. Классическая теория, представляющая свет как электромагнитные волны, не смогла объяснить законы фотоэффекта и эффект Комптона. Явлением внешнего фотоэффекта назы­вается вырывание электронов с поверхности тела под действием света достаточно вы­сокой частоты. Экспериментально были установлены следующие закономерности внешнего фотоэффекта: Максимальная кинетическая энергия фотоэлектронов линейно растет с увеличением частоты света и не зависит от его интенсивности. Для каждого вещества существует т.н. «красная граница» фотоэффекта, т.е., наименьшая частота νМИН, при которой еще возможен фотоэффект. Число фотоэлектронов, вырываемых светом из катода за 1с, прямо пропорционально интенсивности света. Фотоэффект практически безынерционен, фототок возникает практически мгновенно после начала освещения катода при условии, что частота света ν ≥ νМИН . А.Эйнштейн пришел к выводу, что свет распространяется в пространстве и поглощается веществом в виде фотонов – квантов электромагнитного поля с энергией εf = hv.При взаимодействии с веществом фотон целиком передает свою энергию одному электрону. Эта энергия за­трачивается на работу выхода электрона из вещества АВЫХ и сообщение вылетевшему элект­рону кинетической энергии EКИН: (формула Эйнштейна).Это выражение объясняет все экспериментальные законы фотоэффекта. В частности, «красную границу» фотоэффекта, т.е., νМИН= АВЫХ/h. Кроме того, фототок прекращается, т.е. электроны не долетают до анода, при приложении между электродами т.н. задерживающей разности потенциалов . Эффект Комптона состоит в наблюдении у рассеянного на веществе рентгеновского излучения увеличения длины волны. Он не объясним с волновой точки зрения, т.к. согласно ей при прохождении электромагнитной волны через вещество возникает вторичное излучение с той же самой длиной волны. Этот эффект легко объясняется, если его рассматривать как упругое соударение двух частиц: фотона (f) и неподвижного электрона (e) (рассеяние фотона на электроне) и записать законы сохранения импульса и энергии: . Учтем, что энергия электрона после столкновения ; εf=hν=hc/λ и εf’=hν’=hc/λ’ – энергии налетающего и рассеянного фотонов, соответственно; θ – угол рассеяния, т.е. угол между векторами импульсов фотонов . Так как электромагнитная волна, обладаю­щая энергией Е, имеет импульс р = Е/c(это вытекает из общего выражения СТО для энергии при m= 0), то та­кое же соотношение должно выполняться и для импульса фотона:pf= εf/c = hv/c=h/λ=ħ·k, где λ и k=2π/λ - длина волны и модуль волнового вектора , соответственно, ħ=h/2π – тоже постоянная Планка.Решая совместно уравнения получим: , где – т.н. комптоновская длина волны для электрона.Рассматривая свет как поток частиц-фотонов удалось также объяснить давление света на поверхность. Давление света. Фотоны, обладая импульсами, попадая на поверхность, ока­зывают на нее давление. Если п – плотность фотонов, то на единицу поверхности в единицу времени попадает п·с фотонов. При поглощении каждый фотон сообщает поверхности импульс рf = hv/c, тогда все фотоны сообщат единице площади поверхности в единицу времени импульс (а это и есть давление): Р =(hv/c)· п·с= εf ·n. Но величина εf ·nравна энергии фотонов, за­ключенных в единице объема, т.е., объемной плотности электромагнитной энергии w. Таким образом, Р = wили с учетом того, что часть фотонов отражается: Р = w(1+ ρ), где ρ –коэффициент отражения, равный 1 при полном отражении фотонов, и 0 при их полном поглощении. Полученный результат совпадает с выражением для давле­ния света в электромагнитной теории. 3.5. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ. Корпускулярно-волновой дуа­лизм света. Т.о., в одних опытах (дифракция, интерференция, поляризация) свет проявляет волновые свойства, в других же (тепловое излучение, фотоэффект, эффект Комптона) он ведет себя как поток частиц-фотонов, но никогда не проявляет волновые и корпускулярные свойства одновременно. Волновая и квантовая теории света допол­няют друг друга. Двойственная природа света получила название корпускулярно-волнового дуа­лизма света и находит свое выражение в формулах, определяю­щих основные характеристики фотонов. Как видно из этих формул, корпускулярные характеристики фотона – энергия εf = hvиимпульс рf = hv/c=h/λ– связаны с волновыми характеристиками света : его частотой ν и длиной волны λ.Боль­шая группа оптических явлений – интерференция, дифракция, поляризация – полностью объясняется в волновой оптике. Однако, если «перемещаться» от длинных волн в сторону более коротких, то вол­новые свойства света будут проявляться все слабее, уступая место более отчетливо проявляющимся квантовым свойствам. Это видно, например, из существования «красной границы» фотоэффекта и такой же границы для фотохимических реакций. Р ассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллель­ный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, распо­ложенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E0·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропор­циональная интенсивности I(x) вэтой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)E(x) 2.С квантовой точки зрения образование на эк­ране дифракционной картины означает, что при прохождении све­та через щель происходит перераспределениефотонов в пространстве. В результате этого в разные точки экрана попадает различноечисло фотонов. Освещенность экрана в данной точке будет тем больше, чем большей будет суммарная энергия фотонов, попадающих за еди­ницу времени в данную точку. Эта энергия, в свою очередь, пропорциональна числу п(x) фотонов, доставивших эту энергию. Таким образом, I(x) п(x).Из сказанного следует, что E(x) 2

Второе соотношение устанавливает связь между неопределенностью энергии ΔE квазистационарного возбужденного состояния и средним временем жизни Δtвозбужденного состояния в атомных процессах. Например, достаточно точно можно измерить энергию системы в стационарном состоянии, время жизни в котором велико (Δt→ ∞), если же система находится в нестационарном состоянии, время жизни Δt в котором конечно, энергию можно измерить с погрешностью порядка ΔE

, а , то для удельного сопротивления проводника получается . Опыт показывает, что сопротивление от температуры зависит линейно: . Кроме того, классическая теория электропроводности не смогла объяснить явление сверхпроводимости, отсутствие различия в теплоемкостях диэлектриков и металлов. Все это удалось объяснить лишь после создания квантовой физики.

Электрические токи в различных средах.

Ток в жидкостях 

     Если на две пластины, помещённые в жидкость, подать напряжение (подсоединить их к батарейке), то в жидкости между пластинами возникнет электрическое поле. Однако ток пойдёт лишь в том случае, если в жидкости есть свободные электрические заряды. Такие жидкости называются электролитами. К ним, в частности, относятся растворы солей, кислот. Следует отметить, что наличие свободных зарядов (ионов) – свойство самого раствора, воздействие поля здесь ни при чём. Например, медный купорос CuSO4, растворяясь в воде, диссоциирует (разлагается) на положительно заряженные ионы меди Cu++ и отрицательно заряженные ионы кислотного остатка SO4- -. В электрическом поле отрицательные ионы (анионы) станут двигаться к положительному электроду - аноду, положительные ионы (катионы) – к отрицательному электроду – катоду. Через жидкость пойдёт электрический ток. В нашем примере с медным купоросом ионы меди, достигнув катода, нейтрализуются и оседают на нём. Если анод медный, то ионы кислотного остатка,  достигнув анода, нейтрализуются и соединяются с атомами меди (отрывая их от анода), превращаясь в медный купорос. В воде последний диссоциирует, образуя ионы. В результате происходит перенос меди с анода на катод; концентрация раствора при этом не меняется. Поскольку каждый ион несёт и массу, и заряд, а все ионы, двигающиеся в сторону данного электрода, одинаковые, то выделившаяся или осевшая на электроде масса  M всегда будет пропорциональна заряду q, прошедшему через электрод. (Коэффициент пропорциональности k называется электрохимическим эквивалентом вещества.) Это очевидное утверждение известно как закон Фарадея (или закон электролиза): M = k·q.

Электролиз - выделение на электродах составных частей растворённых веществ или других веществ, являющихся результатом вторичных реакций на электродах.

Благодаря тому, что скорость ионов в электрическом поле оказывается пропорциональна напряжённости поля (экспериментальный факт), связь напряжения на электродах и силы тока в электролитах является линейной, то есть в электролитах, как и в твёрдых проводниках, выполняется закон Ома.

Ток в газах                           

Если на два электрода, разделённых газовым промежутком, подать напряжение, то ток в общем случае не пойдёт, так как поле есть, а свободных зарядов нет, газ состоит из нейтральных молекул. Для того, чтобы из этих молекул образовались свободные заряды – положительные ионы и электроны, необходим внешний ионизатор, например, ультрафиолетовая лампа. Излучение такой лампы производит ионизацию части молекул газа, возникает электрический ток. Ионы движутся к катоду, электроны – к аноду. Разряд такого типа, то есть с внешним ионизатором, называется несамостоятельным газовым разрядом.

Если же свободные заряды образуются в газе в процессе самого разряда, без внешней помощи, разряд называется самостоятельным. Например, если в описанном выше несамостоятельном разряде повышать напряжение, кинетической энергии ионов, "бомбардирующих" катод, может оказаться достаточной для выбивания из катода вторичных электронов, которые, набирая энергию в поле, способны произвести ионизацию молекул газа при столкновениях с ними. Несамостоятельный разряд перейдёт в самостоятельный, внешний ионизатор уже будет не нужен.

Виды самостоятельного газового разряда различны в зависимости от типа эмиссии на катоде и типа ионизации молекул газа.
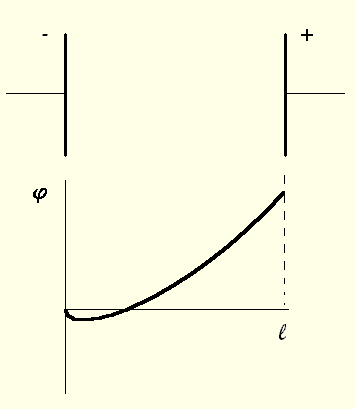
Ток в вакууме     

Если на два электрода, разделённых вакуумным промежутком ℓ, подать напряжение, в промежутке возникнет электрическое поле. Но где взять заряды? Только путём их эмиссии с электродов. Наиболее распространённый тип эмиссии – термоэлектронная эмиссия с катода. Если нагреть катод, электроны в нём получат дополнительную энергию, и часть из них будет способна преодолеть потенциальный барьер на границе металла (совершить работу выхода электрона) и выйти в межэлектродный промежуток.

Попав в электрическое поле, электроны, ускоряясь, движутся к аноду, возникает электрический ток. В вакууме электронам не с чем сталкиваться, они не испытывают сопротивления движению. Казалось бы, при этом сколь угодно малое поле должно вызвать сколь угодно большой ток. Однако, в отличие от тока в средах, где всегда есть почти полная компенсация разноимённых зарядов (проводники электрически нейтральны), в вакууме отрицательный заряд электронного пучка ничем не скомпенсирован. Поэтому электроны движутся в поле, являющимся суперпозицией двух полей: поля, созданного зарядами на электродах и поля объёмного отрицательного заряда электронного пучка. Итоговое распределение потенциала между электродами схематично показано на рисунке.


Вблизи катода, где концентрация электронов велика, существует потенциальный барьер для электронов величиной порядка их средней кинетической энергии (в электронвольтах – kT/e), который пропускает дальше в промежуток только часть электронов, обладающих энергией большей, чем глубина потенциальной ямы. Остальные электроны возвращаются назад. Подобная ситуация носит название "ограничение тока объёмным зарядом". Чем выше напряжение на аноде, тем меньше глубина ямы. Связь плотности тока j с анодным напряжением U получается следующей (e и m – элементарный заряд и масса электрона, соответственно):



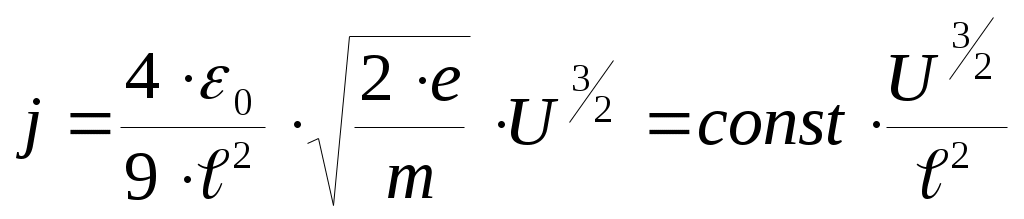
То есть связь тока и напряжения не линейна, как в законе Ома, а определяется по "закону трёх вторых" – именно так в обиходе и называется этот закон. Более "официальное" название закона – закон Ленгмюра-Богуславского.


2.4. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ.

Магнитное поле. Индукция . Сила Ампера

На рисунке приведен ряд опытных фактов: а) намагничен­ная стрелка компаса указывает на север; б) два намагниченных куска железа (два постоянных магнита) отталкиваются при сбли­жении одноименными полюсами; в) провод с током действует на магнитную стрелку компаса (опыт Эрстеда) ; г) постоянный маг­нит действует на п 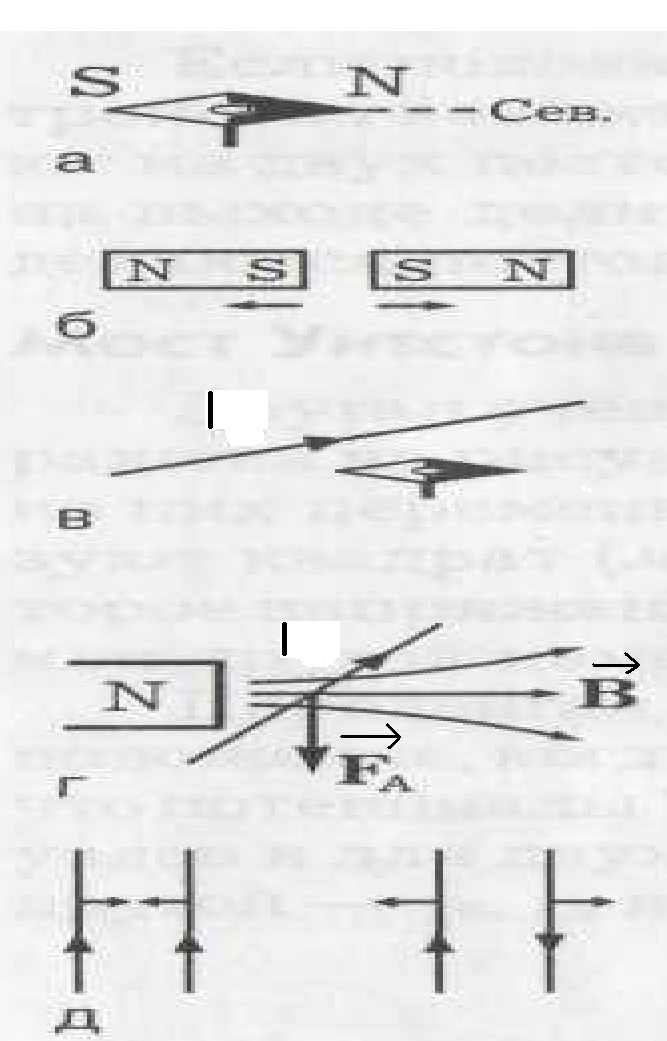ровод с током (сила Ампера); д) два провода с одинаковым направлением тока притягиваются друг к другу, а с противоположно направленными токами – отталкиваются . Этот тип взаимодействия отличается от взаимодействия зарядов в электростатике тем, что силы возникают между намагниченными телами и движущи­мися зарядами.

Физическая система, распределенная в пространстве, в которой обнаруживаются силы, действующие на намагниченные тела или про­вода с током, называется магнитным полем.

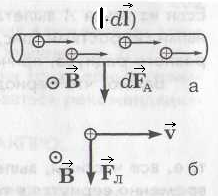
К 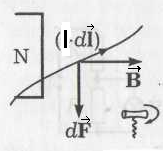оличественно перечисленные явления описываются следующим образом. Выделим в проводе с током I участок dlи будем считать его вектором , направленным по току. Про­изведение (I· ) будем называть элементом тока. Магнитное поле в некоторой точке ха­рактеризуется вектором , который получил название магнитной индукции. Это такой вектор, который направлен от северного полю­са магнита к южному (вне магнита) и который, будучи умножен векторно на вектор (I· ), дает силу, действующую на этот элемент, причем и по величине, и по направлению . Это т.н. сила Ампера. Квадратные скобки означают векторное произведение. Для определения направления можно использовать правило правого буравчика. Если рукоятку вращать от первого вектора-сомножителя (I· ) ко второму , то направле­ние поступательного движения буравчика укажет на направ­ление вектора (рис.). Можно использовать и правило левой руки: если поставить левую руку так, чтобы силовые линии входи­ли в ладонь, а четыре пальца указывали направление тока, то ото­гнутый большой палец укажет направление силы. Абсолютная величина dFравна

dF = I·dℓ·В · sinα, где α – угол между (I· ) и .

Если α= 90° и поле однородно, то можно перейти от формулы для бесконечно малых к формуле: F=I·ℓ·B, из которой можно получить единицу для измерения магнитной индукции В. Если I=1А,ℓ=1 м, а сила F= 1 Н, то В будет равно 1 Тесла: 1 Тл = 1 Н/(А·м), т. е. это индукция такого магнитного поля, которое действует на провод длиной 1 м с током 1 А силой в 1 Н.

Рамка с током в магнитном поле


Н а практике часто встречается такое использо­вание силы Ампера: между полюсами магнита по­мещают прямоугольную рамку из провода, по которому течет ток Используя правило левой руки, находим, что на левый участок провода действу­ет сила, направленная от нас, а на правый участок – к нам (рис.).

В результате рамка будет поворачиваться.

Механический момент силы, действующий на одну сторону рамки , на обе стороны . Поскольку в нашем случае с рамкой , можно просто написать М = 2·r·Fили, воспользовавшись упрощенной формулой для силы Ампера,:M = 2·r·F = 2·r·I·ℓ·B = I·S·B, где S= 2·r·ℓ – площадь рамки.

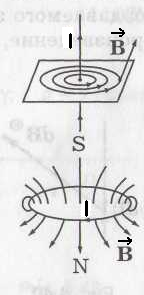
Произведение I·Sназываетсямагнитным мо­ментом ртрамки с током. Если рассматривать магнитный момент как вектор , направленный по нормали к плоскости рамки, то можно записать для : .



Магнитное поле, создаваемое проводом с током. Закон Био – Савара – Лапласа.
Если пропустить прямой провод с током I через лист фанеры, на котором насыпаны железные опилки, то окажется, что сило­вые линии около провода с током, вдоль которых располагаются маленькие магнитики-опилки, направлены всюду перпендикулярно этому току и представляют собой концентрические окружности (рис.). Их направление оп­ределяется по правилу правого буравчика.

Если ток круговой, то силовые линии со­здаваемого им поля будут такими, как показа­но на нижнем рисунке . Круговой ток – это элементарный магнит. Северным полюсом N магнита считается та сторона, откуда силовые линии выходят, южным S– куда силовые линии входят.

Б 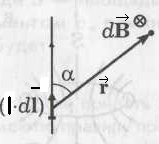ио, Саваром и Лапласом было показано, что магнитное поле , создаваемое эле­ментом тока (I· ) на рас­стоянии r, следует находить по формуле: , где – коэффициент пропорциональности, μ0 = 4л·10-7Гн/м – магнитная постоянная. Согласно этой формуле, поле зависит не только от величины тока, создающего поле, и расстояния до точки наблюдения, но и от взаимного расположения векторов (I· ) и , т. е. от угла α (рис.). Сравним это выражение с аналогичным в случае электростатического поля, где , создаваемое зарядом dq, находилось по формуле: , но там вектор был параллелен . В случае магнитного поля направление перпендикулярно и сильно зависит от угла α. Для магнитного поля также справедлив принцип суперпозиции: магнитное поле, созданное не­сколькими токами, равно векторной сумме маг­нитных полей, создаваемых каждым током в от­дельности: .

П 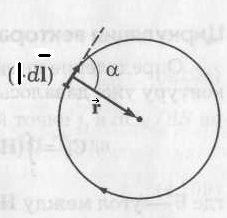оле в центре кругового тока (рис.).
Определяя направление в центре окружности, мы видим, что все векторы , создаваемые в этой точке всеми участками , направлены одинаково (на рис. – от нас за чертеж). Следовательно, для нахождения обще­го можно просто все элементы dB складывать арифметически, так как для них α = 90°: .
П 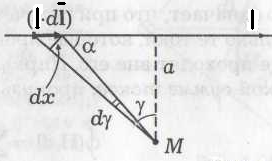оле бесконечного прямого провода на расстоянии а от него (рис. ). В этом случае все векторы , создаваемые всеми уча­стками в т.М, тоже направлены одинаково (от нас за чертеж), и их можно просто ариф­метически суммировать (интегрировать). Но теперь для каждого участка величины α и r будут разными. Для взятия интеграла удобнее все переменные свести к углу γ, провести интегрирование по γ от 0 до π/2 и результат удвоить: .
Ц 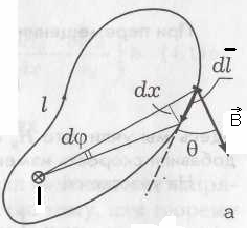иркуляция вектора по замкнутому контуру

Определение циркуляции CА некоторого вектора по замкнутому контуру ℓ уже давалось в разделе «Электростатика». Для она запишется так:

, где θ – угол между и (рис.) .

Рассмотрим случай, когда контур охватывает ток I.

Будем для простоты считать, что магнитное поле созда­ется прямолинейным проводом с током I, направленным перпендикулярно рис. и от нас, т. е. в любой точке . При повороте на малый угол dφ: dx=a·dφ ; dx/dℓ=cosθ. Подставив под знак интеграла, получим : .

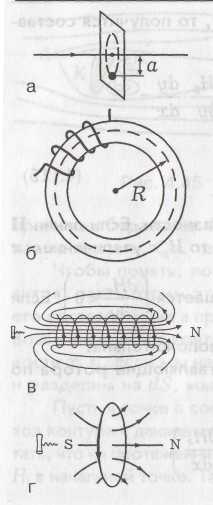Если замкнутый контур охватывает несколько токов, то под I понимается алгебраическая сумма токов и теорему о циркуляции вектора можно сформулировать так: Циркуляция вектора равна алгеб­раической сумме токов, пронизывающих контур, умноженной на магнитную постоянную μ0 : .

Эту формулу удобно использовать для нахождения магнитной индукции В в различных случаях аналогично тому, как теорему Гаусса было удобно использовать для нахождения напряженно­сти электрического поля Е. Рассчитаем индукцию магнитного поля внутри тороида и длинного соленоида.

На рисунке б изображен тороид, на который намотано N витков провода с токомI. Если выбрать контур по оси тороида (пунк­тир на рис.), где магнитное поле однородно, то : , откуда получим: . Из этого выражения найдем магнитную индукцию внутри длинной катушки – соленоиде, если ее рассматривать как часть очень большого тороида: B=μ0·n·I , где – густота намотки .




Сила Лоренца. Движение заряженной частицы в магнитном поле
Ранее рассматривалась сила Ампера, действующая на эле­мент тока (I· ), в поле : (рис. а). Она является суммарной силой, действующей на все движущиеся по проводнику заряды. Найдем силу, действующую на отдельный малый заряд dq. Она получила название силы Лоренца (рис.б). Представим (I·dℓ) в виде (dq/dt)·dℓ =dq·υ. Тогда

, а для точечного заряда q:

Е 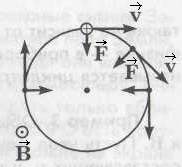е направление определяется так же, как и направление силы Ампера (правило правого винта или левой руки). Важно отме­тить, что , как и всякое векторное произведение, перпендикуляр­на и . Это означает, что работа этой силы всегда равна нулю. Сила Лоренца может отклонять заряженную частицу, но не может изменить ее кинетическую энергию.

а). Скорость частицы параллельна полю ( || ). В этом слу­чае = 0 и поле на движение частицы не влияет. Частица движется равномерно и прямолинейно.

б). . В этом случае FЛ = q·υ·Bи перпендикулярна к плоскости, в которой лежат и . Она заставляет части­цу заворачивать, играя роль центростремительной силы, обеспечива­ющей центростремительное ускорение

ацс = υ2/R. Уравнение движения будет иметь вид: ,
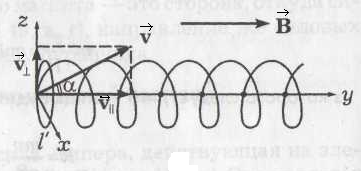из которого следует, что частица будет двигаться по окружности радиуса: , т.е. радиус окружности зависит от скорости частицы и ее удельного заряда (q/m).

в). Скорость направлена под некоторым углом к . Если разложить скорость на две составляющие: одну в направлении поля , а другую перпендикулярно ему, то сложение двух движений: равномерного вдоль поля и вращения по окружности вокруг поля приводит к траектории в виде спирали (рис.)
Магнитный поток. Теорема Гаусса

Определение потока вектора через некоторую поверх­ность Sбыло дано в разделе «Электростатика». Поток вектора обозначим через Ф: .

Для однородного поля и плоской поверхности можно написать Ф = B·S·cosα , где α – угол между нормалью к площадке и векто­ром . В случае, когда перпендикулярно площадке, поток Ф = B·S. Единица потока – 1 Тл·м2 называется

Вебер (Вб).

Пусть магнитное поле в соленоиде (катушке) создается то­ком I. Величины В и Ф пропорциональны силе создающего их тока: Ф =L·I .Коэффициент пропорциональности L измеряется в генри (1 Гн = 1 Вб/1 А) и носит название индуктивности.

Для электрического поля, согласно теореме Гаусса, поток вектора через замкну­тую поверхность равен заряду, заключенному внутри этой поверхности ФD= q.

Ч 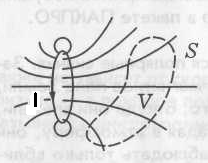то же касается магнитных зарядов, то их не существует, источ­ником магнитного поля являются токи. Силовые линии нигде не начинаются и не кончаются, они замкнуты сами на себя. Поэтому теорема Гаусса для магнитного поля в вакууме звучит так: поток вектора через замкнутую поверхность всегда ра­вен нулю (сколько силовых линий входит в поверхность, столько же и выходит, рис. ): .
Работа по перемещению провода с током в магнитном поле

П
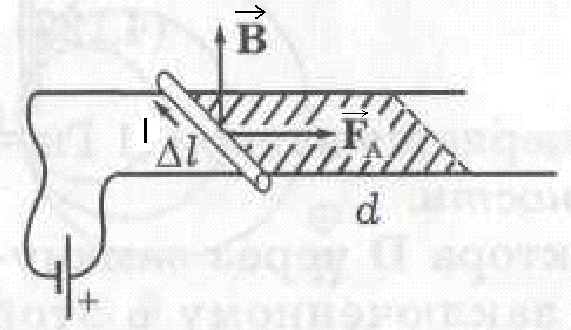
усть имеются два металлических рельса, по которым мо­жет скользить металлический стержень (рис.). Если к рельсам подключить источник тока и поместить все в магнит­ное поле , как показано на рисунке, то на стержень будет действовать сила Ампера FА. Она, передвигая стержень, мо­жет совершить работу: А = FA·d = I·Δℓ·B·d= I·B·ΔS=I·ΔΦ , или в дифференциальной форме : dA=I·dФ. где Δ(d)Φ – это изменение потока Ф вектора через заштрихованную площадку, т.е., через контур с током. Т.о., работа силы Ампера в магнитном поле равна произведе­нию силы тока на изменение магнит­ного потока через контур.
1   ...   5   6   7   8   9   10   11   12   ...   19

Смотрите также файлы