Файл: Минимальный курс физики. Составлен доц. Юнусовым Н. Б.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 380
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
. Из этой же формулы следует, что со скоростью света может двигаться, обладая конечным импульсом, только безмассовая частица (m=0). Это, например, фотон.
Основное уравнение динамики в СТО принимает, т.о., вид:
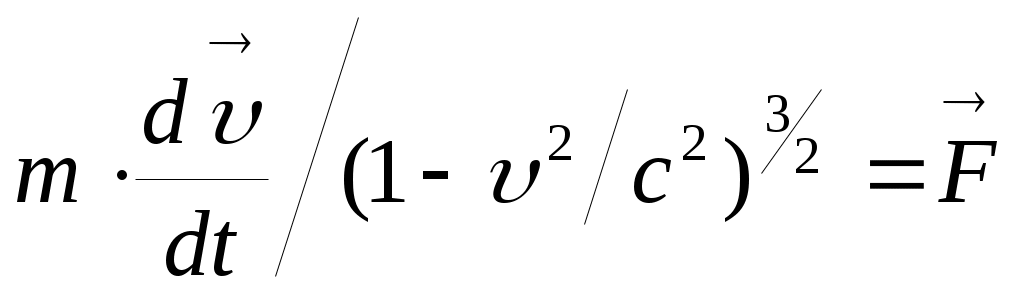 .
.
Если сила совершает работу, разгоняя тело от нулевой скорости до некоторой релятивистской скорости
совершает работу, разгоняя тело от нулевой скорости до некоторой релятивистской скорости  , то эта работа целиком идет на создание кинетической энергии, т.е.:
, то эта работа целиком идет на создание кинетической энергии, т.е.: 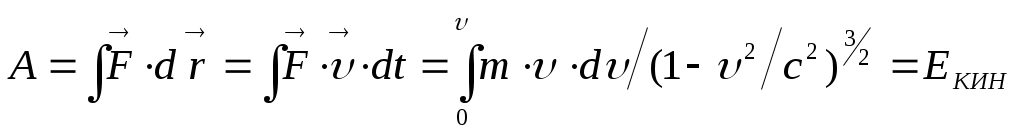 . Вычисление интеграла приводит к выражению:
. Вычисление интеграла приводит к выражению:  .
.
Если истолковывать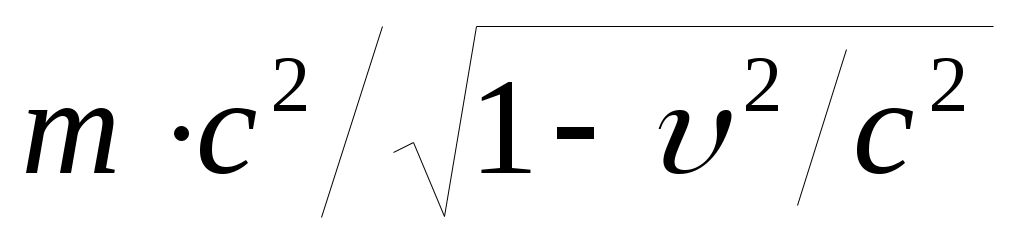 как полную энергию
как полную энергию 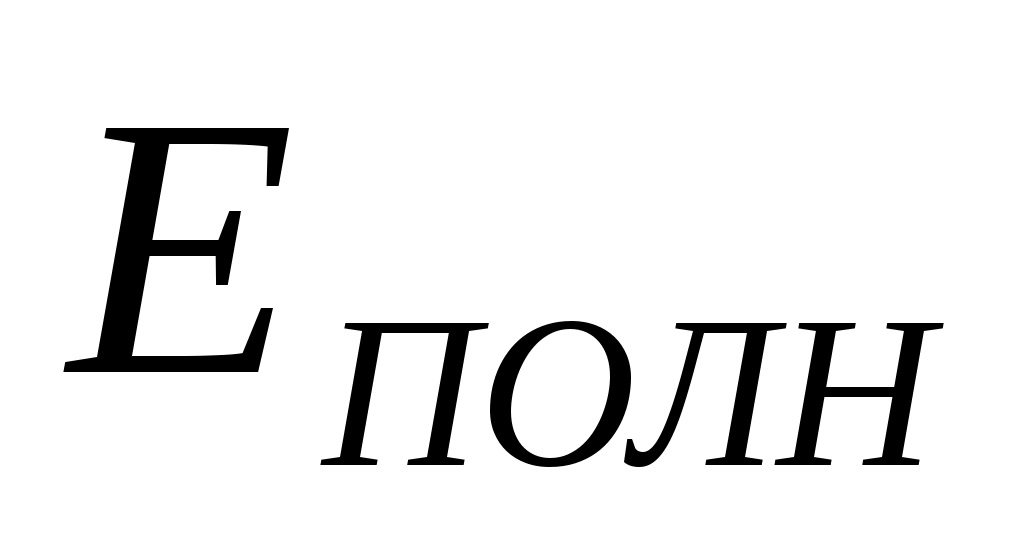 тела, то отсюда следует, что когда тело покоится и его кинетическая энергия равна нулю, оно тем не менее обладает энергией т·с2. В соответствии с этим т·с2называют энергией покоя тела : Е0 = m·c2. Это знаменитая формула Эйнштейна, говорящая о том, что масса тела является не только мерой инертности или мерой гравитационного действия, но и мерой энергосодержания тела. Используя выражения для импульса и энергии тела можно получить еще одно часто используемое выражение для полной энергии тела:
тела, то отсюда следует, что когда тело покоится и его кинетическая энергия равна нулю, оно тем не менее обладает энергией т·с2. В соответствии с этим т·с2называют энергией покоя тела : Е0 = m·c2. Это знаменитая формула Эйнштейна, говорящая о том, что масса тела является не только мерой инертности или мерой гравитационного действия, но и мерой энергосодержания тела. Используя выражения для импульса и энергии тела можно получить еще одно часто используемое выражение для полной энергии тела:
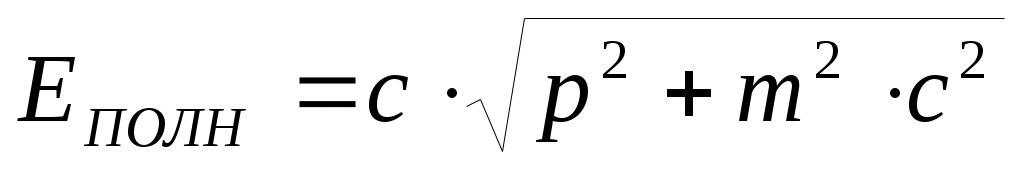 .
.
Согласно СТО, пространство и время являются относительными, зависят друг от друга, образуя единый 4-х мерный пространственно-временной континуум.
Несколько позже в общей теории относительности А. Эйнштейн показал, что на пространство и время влияет тяготение, а именно, вблизи очень массивных тел пространство искривляется, а время замедляется.
1.6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Д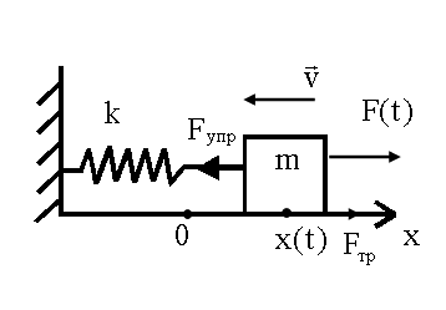 вижение, которое повторяется через равные
вижение, которое повторяется через равные
промежутки времени, называется колебательным. Промежуток времени T, по истечение которого движение повторяется, называется периодом колебания. В моменты времени tи t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/Т. Она определяет, сколько раз в секунду повторяется движение, и измеряется в герцах(Гц). Круговой (циклической) частотой называется величина ω = 2πv.
Свободные (собственные) колебания – колебания, происходящие без внешних воздействий за счет первоначально полученной телом энергии. Рассмотрим горизонтальный пружинный маятник жесткостью k и массой m, помещенный в среду с коэффициентом сопротивления r, на который вдоль оси х действует переменная внешняя сила F(t), изменяющаяся со временем, например, по гармоническому закону F(t) = F0 ·cosΩt с некоторой частотой Ω .
Уравнение движения маятника:
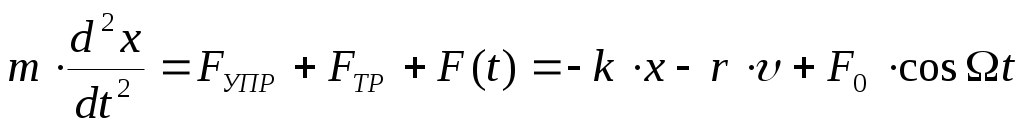 (1), где сила упругости FУПР пропорциональна смещению х, а сила трения (сопротивления) FТР среды – скорости υ=dx/dt. Перепишем (1) по другому:
(1), где сила упругости FУПР пропорциональна смещению х, а сила трения (сопротивления) FТР среды – скорости υ=dx/dt. Перепишем (1) по другому:
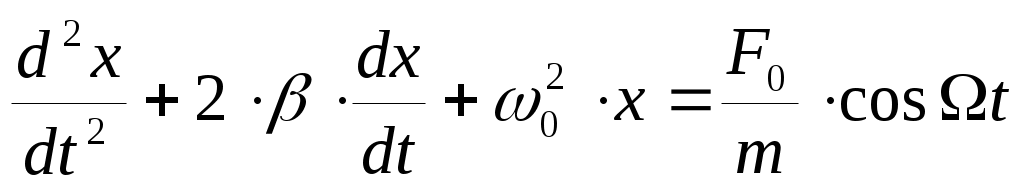 (2),
(2),
где введены обозначения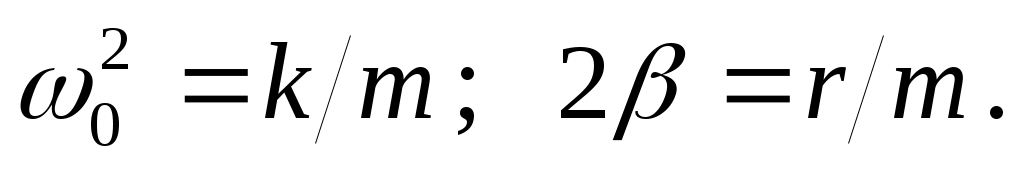
Проанализируем уравнение (2).
A
2.
В случае сильного затухания (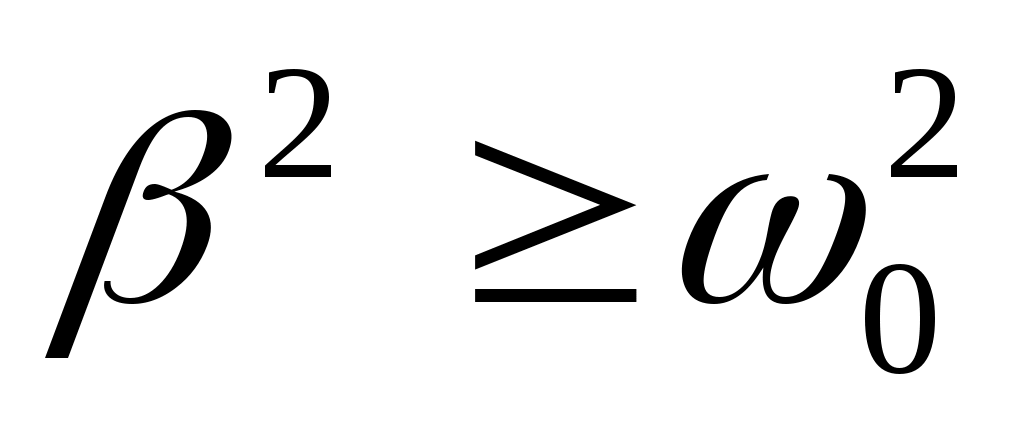 ) колебательный процесс не развивается: система, выведенная из состояния равновесия и предоставленная самой себе, просто медленно возвращается к нему. Это т.н. апериодический процесс.
) колебательный процесс не развивается: система, выведенная из состояния равновесия и предоставленная самой себе, просто медленно возвращается к нему. Это т.н. апериодический процесс.
3. Вынужденные колебания. Резонанс.
Для того чтобы возбудить в системе незатухающие колебания, необходимо компенсировать потери энергии, обусловленные трением (сопротивлением). Такая компенсация может производиться внешними по отношению к колебательной системе источниками энергии. Простейшим случаем является воздействие на систему переменной внешней силы F(t). Под влиянием этой силы в системе возникнут колебания, происходящие в такт с изменением силы; эти колебания называются вынужденными.
Дифференциальное уравнение вынужденных колебаний имеет вид (2):
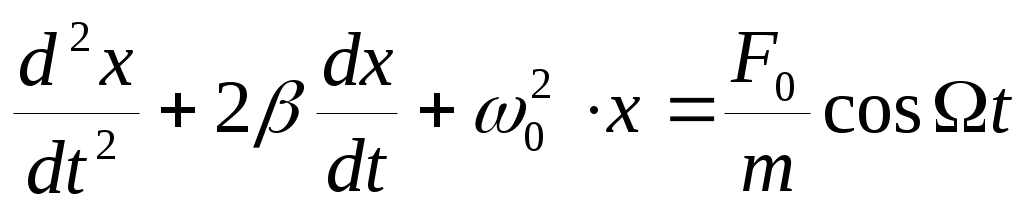 (12).
(12).
Это уравнение является линейным неоднородным дифференциальным уравнением 2 порядка; его общее решение представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения есть решение уравнения колебаний с затуханием, рассмотренное ранее. Рассмотрим частное решение неоднородного уравнения: x =A·cos(Ωt –φ ) (13), описывающее установившиеся колебания с частотой Ω вынуждающей силы.
Величины амплитуды Aи сдвига фазы φ по отношению к фазе вынуждающей силы зависят от соотношения между собственной частотой ω0 системы и Ω, а также от затухания, действующего в системе:
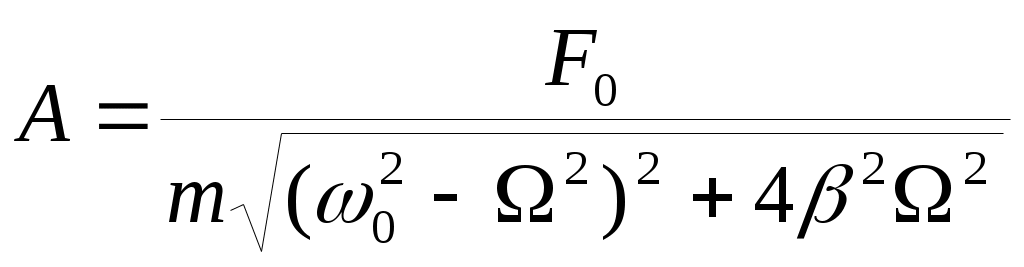 ;
; 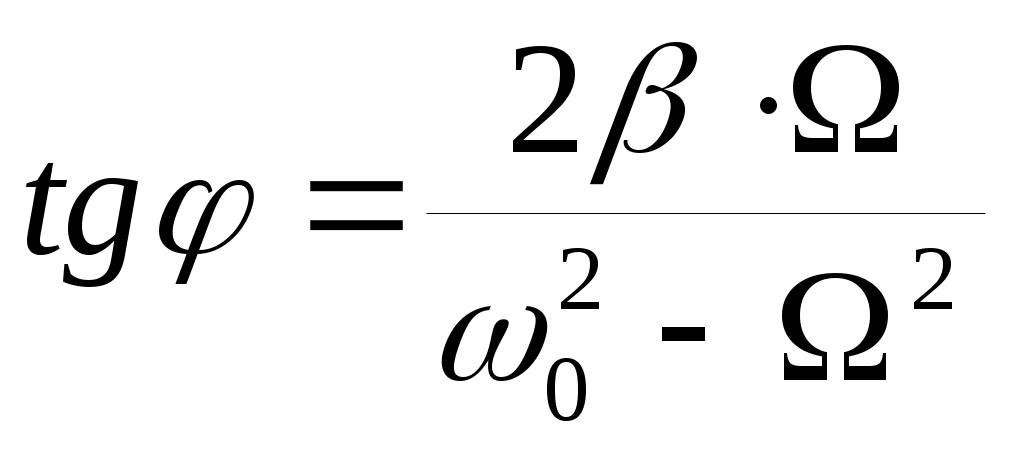 (14).
(14).
П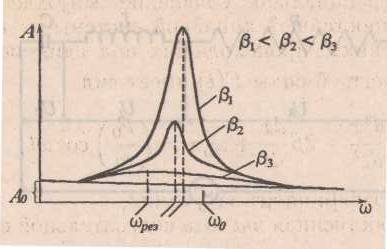 ри некоторой частоте Ω
ри некоторой частоте Ω
0вынуждающей силы амплитуда вынужденных колебаний достигает максимума. Это явление называется резонансом (резонансом смещения). На рис. изображены резонансные кривые для трех значений коэффициента затухания β. Частота ωрез = Ω0 называется резонансной частотой. Ее значение можно найти, исследовав на минимум подкоренное выражение для A в формуле (14):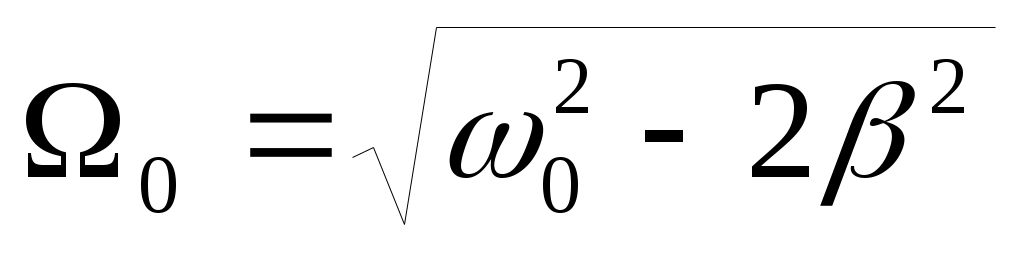 (15).
(15).
Амплитуда при резонансе получается подстановкой Ω0 в выражение для амплитуды:
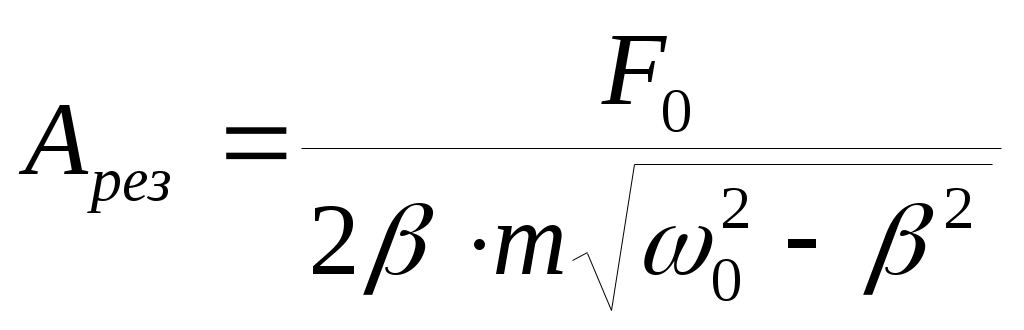 (16).
(16).
Явление распространения колебаний в пространстве называется волновым движением или волной.
Уравнение волны выражает зависимость смещения Ψ колеблющейся точки, участвующей в волновом процессе, от ее координаты х и времени t.
Волна называется продольной, если колебания частиц происходят вдоль линии распространения волны; если колебания частиц перпендикулярны к направлению распространения волны, то волна называется поперечной.
Геометрическое место точек, до которых к некоторому моменту времени дошло колебание, называется фронтом волны. Можно также в среде выделить геометрическое место точек, колеблющихся в одинаковых фазах. Эта совокупность точек образует поверхность одинаковых фаз или волновую поверхность. Форма фронта волны определяет тип волн, например, у сферической волны фронт представляет собой сферу.
Скорость распространения волны есть скорость распространения данной фазы (волновой поверхности). Ее называют фазовой скоростью υ волны.
Расстояние, на которое определенная фаза колебания распространяется за один период Т колебания, называется
Основное уравнение динамики в СТО принимает, т.о., вид:
Если сила
Если истолковывать
Согласно СТО, пространство и время являются относительными, зависят друг от друга, образуя единый 4-х мерный пространственно-временной континуум.
Несколько позже в общей теории относительности А. Эйнштейн показал, что на пространство и время влияет тяготение, а именно, вблизи очень массивных тел пространство искривляется, а время замедляется.
1.6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Д
 вижение, которое повторяется через равные
вижение, которое повторяется через равные
промежутки времени, называется колебательным. Промежуток времени T, по истечение которого движение повторяется, называется периодом колебания. В моменты времени tи t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/Т. Она определяет, сколько раз в секунду повторяется движение, и измеряется в герцах(Гц). Круговой (циклической) частотой называется величина ω = 2πv.
Свободные (собственные) колебания – колебания, происходящие без внешних воздействий за счет первоначально полученной телом энергии. Рассмотрим горизонтальный пружинный маятник жесткостью k и массой m, помещенный в среду с коэффициентом сопротивления r, на который вдоль оси х действует переменная внешняя сила F(t), изменяющаяся со временем, например, по гармоническому закону F(t) = F0 ·cosΩt с некоторой частотой Ω .
Уравнение движения маятника:
где введены обозначения
Проанализируем уравнение (2).
- 1 2 3 4 5 6 7 8 9 ... 19
Свободные гармонические незатухающие колебания.
 Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
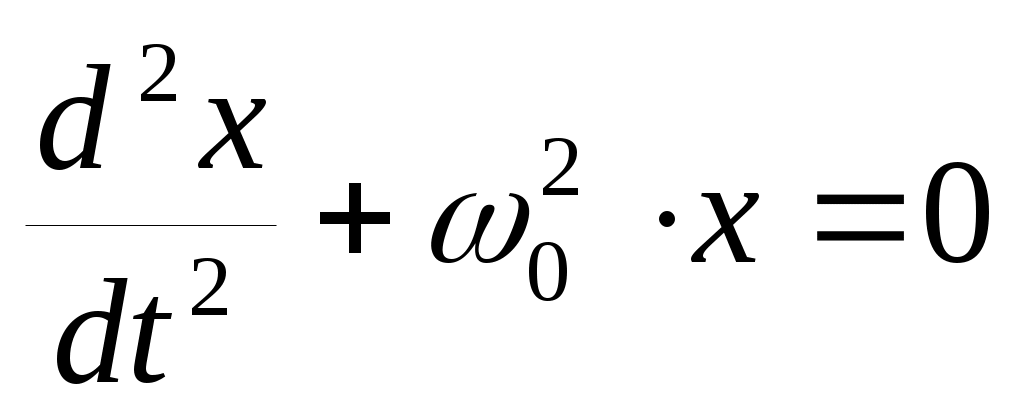 (3).
(3).
Его решением является гармоническая функция: 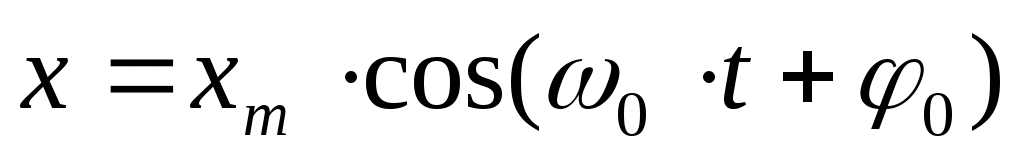 (4),
(4),
в чем легко убедиться, подставив (4) в (3).
В (4) xm , ω0 и φ0 – постоянные величины. xm– амплитуда – величина, указывающая максимальное значение координаты х при отклонении от положения равновесия, ω0 – собственная частота, аргумент косинуса 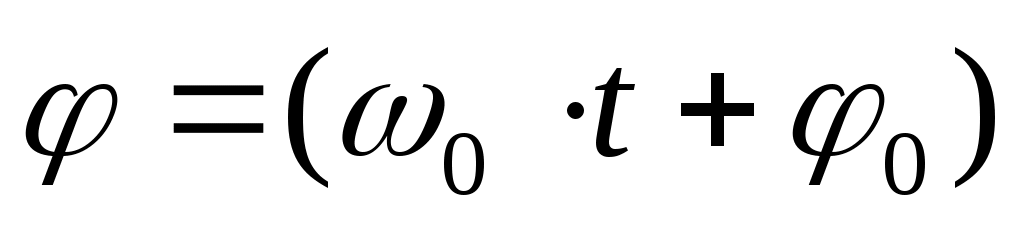 носит название фазы колебания; φ0 — начальная фаза колебания (в момент t= 0).
носит название фазы колебания; φ0 — начальная фаза колебания (в момент t= 0).
Частота колебаний зависит только от свойств колеблющейся системы, но не от амплитуды, а амплитуда и начальная фаза колебаний определяются начальными условиями ее движения, выводящими систему из состояния покоя.
Скорость колеблющейся частицы равна: 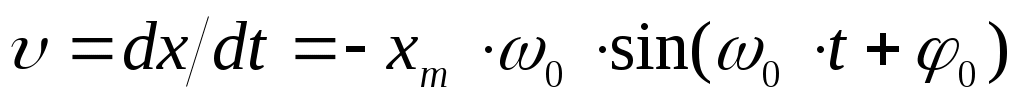 (5).
(5).
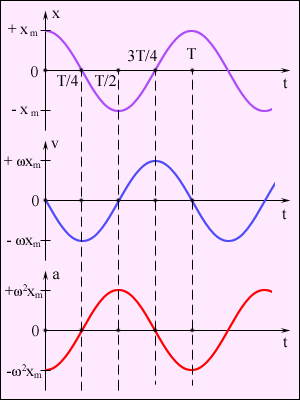
Ускорение частицы при таком движении: 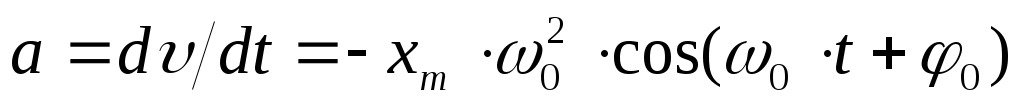 (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0=0.
(6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0=0.
Складывая кинетическую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы:
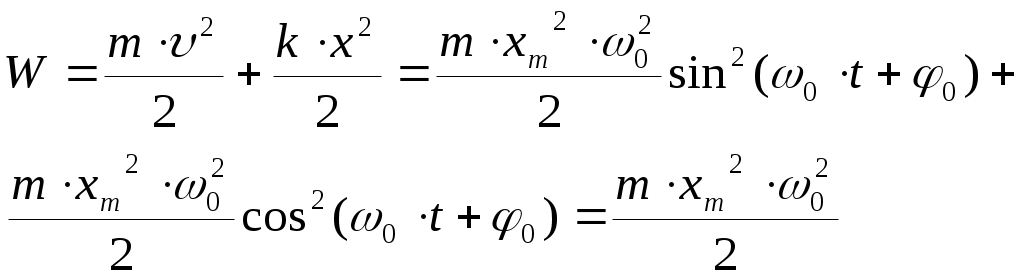 (7).
(7).
Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потенциальная энергии изменяются со временем, как sin2(ω0·t+φ0) и cos2(ω0·t+φ0) , так что когда одна из них увеличивается, другая – уменьшается, т.е. процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения частицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x , действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса).
Примечание: В механике обычно рассматривают колебания : – математического маятника с периодом 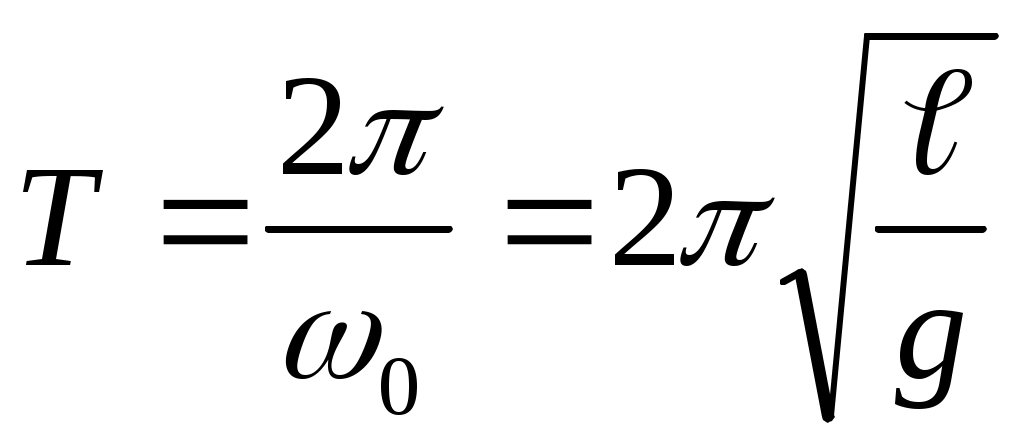 , где ℓ–длина маятника;
, где ℓ–длина маятника;
– физического маятника с периодом 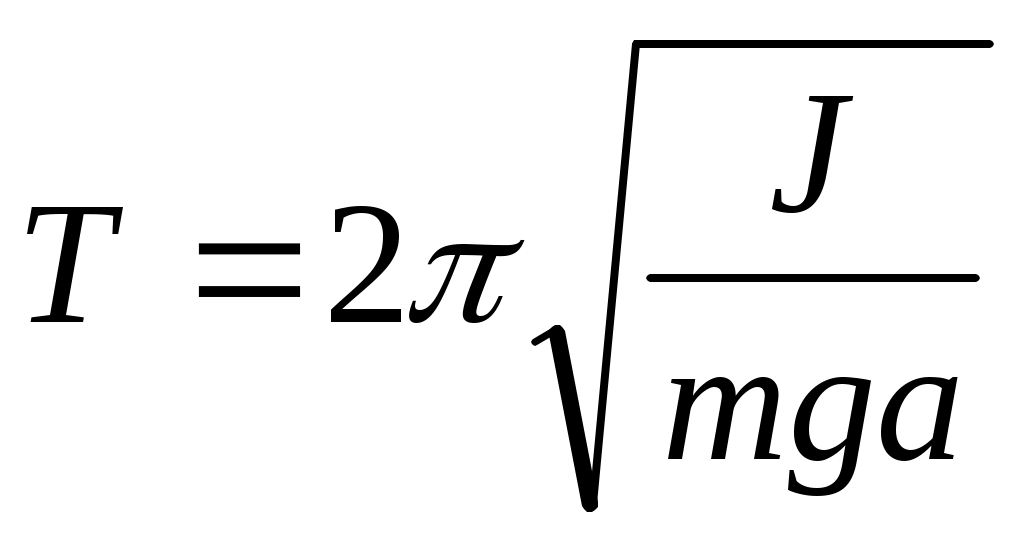 , где J–момент инерции маятника, a–расстояние от точки подвеса маятника до его центра масс;
, где J–момент инерции маятника, a–расстояние от точки подвеса маятника до его центра масс;
– пружинного маятника с периодом 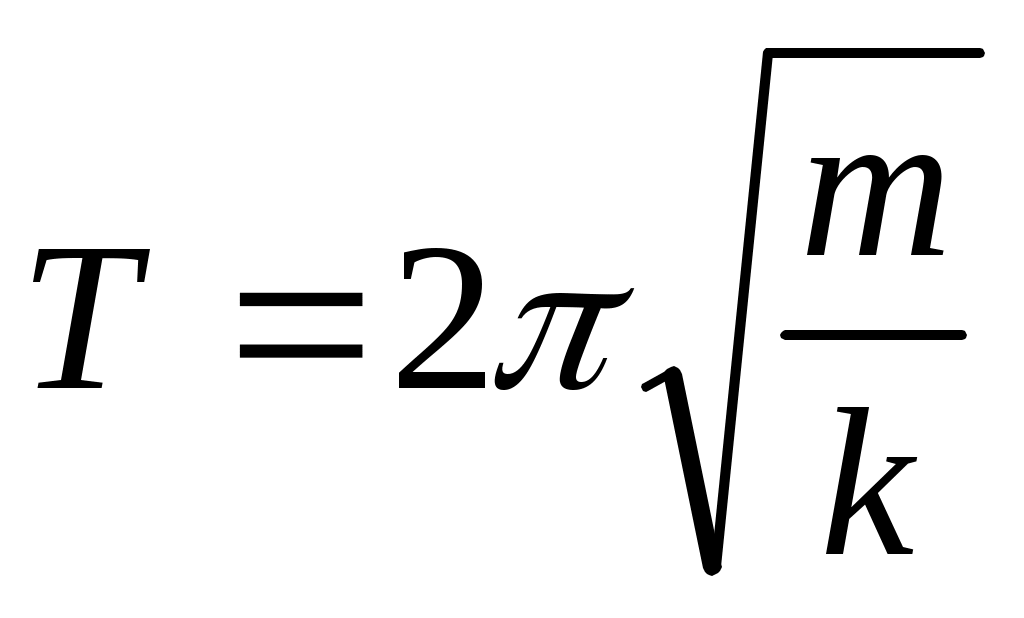 , где k–жесткость пружины.
, где k–жесткость пружины.
2. Свободные затухающие колебания
При наличии силы трения (r ≠0) и отсутствии внешней периодической силы (F0 =0) уравнение движения имеет вид: 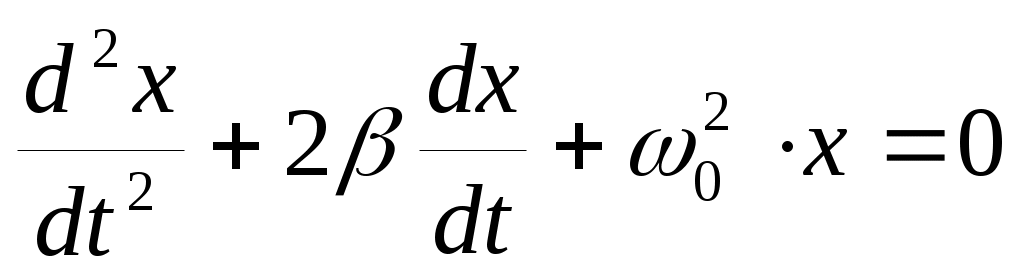 (8),
(8),
г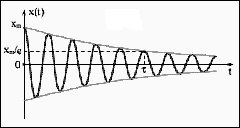
де β называется коэффициентом затухания колебаний. В случае слабого затухания (β – мало) решением такого дифференциального уравнения является функция : 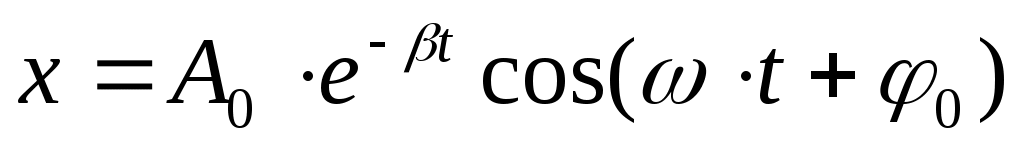 (9). В этом можно убедиться прямой подстановкой (9) в уравнение (8).
(9). В этом можно убедиться прямой подстановкой (9) в уравнение (8). 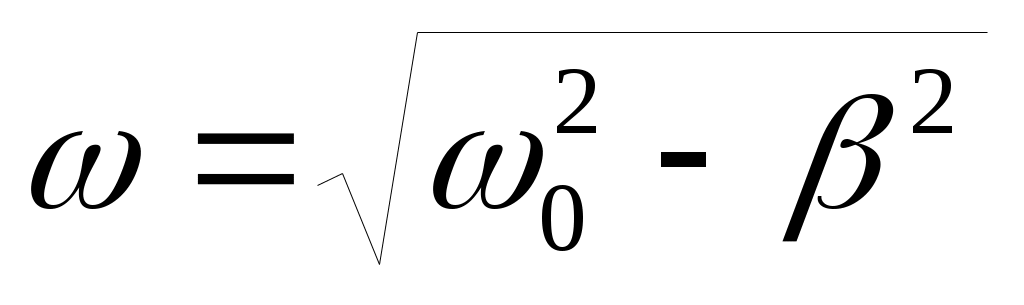 – частота колебаний системы с затуханием. A=A0·e-βt – амплитуда затухающих колебаний.
– частота колебаний системы с затуханием. A=A0·e-βt – амплитуда затухающих колебаний.
Таким образом, амплитуда колебаний убывает по экспоненциальному закону. Вместе с амплитудой убывает также и энергия колебаний W, т.к. W
A2.
Степень убывания амплитуды определяется коэффициентом затухания β. Время τ=1/β, за которое амплитуда колебаний уменьшается в е=2.7183 раз, называют постоянной времени затухания колебаний.
Скорость уменьшения амплитуды за период характеризует величина θ, называемая логарифмическим декрементом затухания. По определению:
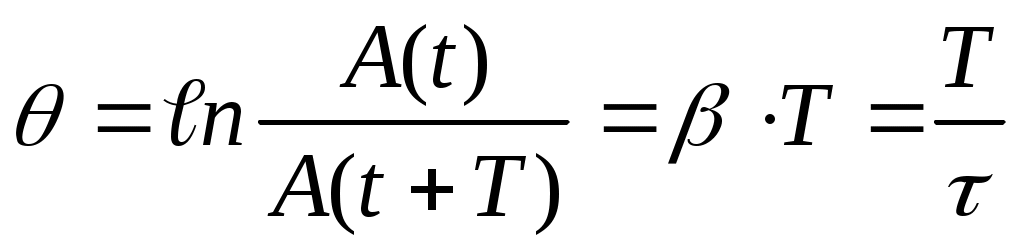 (10).
(10).
Скорость убывания энергии в системе с затуханием характеризует добротность Q:
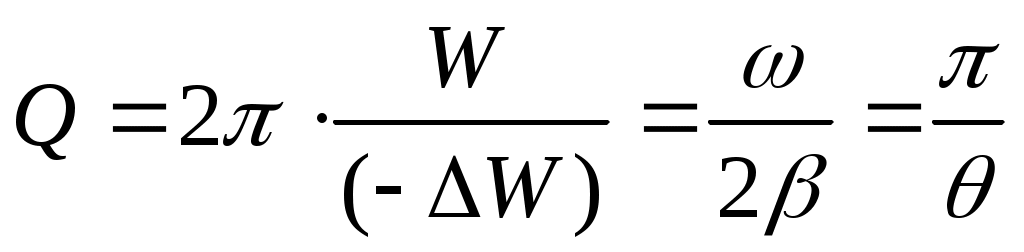 (11),
(11),
где W – энергия, запасенная в системе, (–ΔW)– энергия, теряемая системой за период. Добротность показывает, во сколько раз энергия, запасенная в системе, больше энергии, теряемой за период. Добротность в (11) выражена через параметры системы и логарифмический декремент затухания θ, с учетом того, что W
A
Свободные гармонические незатухающие колебания.
 Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: Его решением является гармоническая функция:
в чем легко убедиться, подставив (4) в (3).
В (4) xm , ω0 и φ0 – постоянные величины. xm– амплитуда – величина, указывающая максимальное значение координаты х при отклонении от положения равновесия, ω0 – собственная частота, аргумент косинуса
Частота колебаний зависит только от свойств колеблющейся системы, но не от амплитуды, а амплитуда и начальная фаза колебаний определяются начальными условиями ее движения, выводящими систему из состояния покоя.
Скорость колеблющейся частицы равна:
Ускорение частицы при таком движении:
Складывая кинетическую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы:
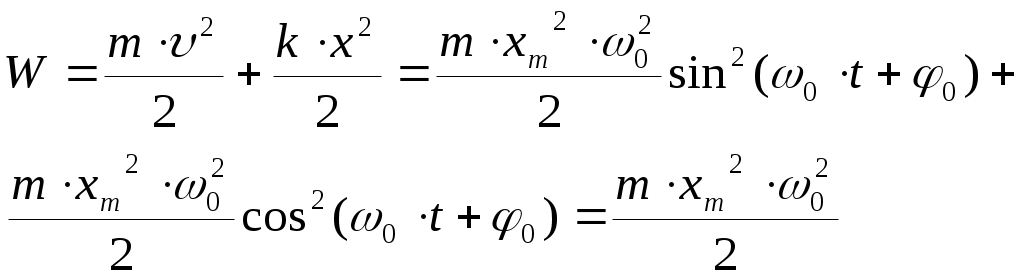 (7).
(7).Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потенциальная энергии изменяются со временем, как sin2(ω0·t+φ0) и cos2(ω0·t+φ0) , так что когда одна из них увеличивается, другая – уменьшается, т.е. процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения частицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x , действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса).
Примечание: В механике обычно рассматривают колебания : – математического маятника с периодом
– физического маятника с периодом
– пружинного маятника с периодом
2. Свободные затухающие колебания
При наличии силы трения (r ≠0) и отсутствии внешней периодической силы (F0 =0) уравнение движения имеет вид:
г

де β называется коэффициентом затухания колебаний. В случае слабого затухания (β – мало) решением такого дифференциального уравнения является функция :
Таким образом, амплитуда колебаний убывает по экспоненциальному закону. Вместе с амплитудой убывает также и энергия колебаний W, т.к. W
2.
В случае сильного затухания (
3. Вынужденные колебания. Резонанс.
Для того чтобы возбудить в системе незатухающие колебания, необходимо компенсировать потери энергии, обусловленные трением (сопротивлением). Такая компенсация может производиться внешними по отношению к колебательной системе источниками энергии. Простейшим случаем является воздействие на систему переменной внешней силы F(t). Под влиянием этой силы в системе возникнут колебания, происходящие в такт с изменением силы; эти колебания называются вынужденными.
Дифференциальное уравнение вынужденных колебаний имеет вид (2):
Это уравнение является линейным неоднородным дифференциальным уравнением 2 порядка; его общее решение представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения есть решение уравнения колебаний с затуханием, рассмотренное ранее. Рассмотрим частное решение неоднородного уравнения: x =A·cos(Ωt –φ ) (13), описывающее установившиеся колебания с частотой Ω вынуждающей силы.
Величины амплитуды Aи сдвига фазы φ по отношению к фазе вынуждающей силы зависят от соотношения между собственной частотой ω0 системы и Ω, а также от затухания, действующего в системе:
П
 ри некоторой частоте Ω
ри некоторой частоте Ω
0вынуждающей силы амплитуда вынужденных колебаний достигает максимума. Это явление называется резонансом (резонансом смещения). На рис. изображены резонансные кривые для трех значений коэффициента затухания β. Частота ωрез = Ω0 называется резонансной частотой. Ее значение можно найти, исследовав на минимум подкоренное выражение для A в формуле (14):
Амплитуда при резонансе получается подстановкой Ω0 в выражение для амплитуды:
-
-
1.7. МЕХАНИЧЕСКИЕ ВОЛНЫ.
Явление распространения колебаний в пространстве называется волновым движением или волной.
Уравнение волны выражает зависимость смещения Ψ колеблющейся точки, участвующей в волновом процессе, от ее координаты х и времени t.
Волна называется продольной, если колебания частиц происходят вдоль линии распространения волны; если колебания частиц перпендикулярны к направлению распространения волны, то волна называется поперечной.
Геометрическое место точек, до которых к некоторому моменту времени дошло колебание, называется фронтом волны. Можно также в среде выделить геометрическое место точек, колеблющихся в одинаковых фазах. Эта совокупность точек образует поверхность одинаковых фаз или волновую поверхность. Форма фронта волны определяет тип волн, например, у сферической волны фронт представляет собой сферу.
Скорость распространения волны есть скорость распространения данной фазы (волновой поверхности). Ее называют фазовой скоростью υ волны.
Расстояние, на которое определенная фаза колебания распространяется за один период Т колебания, называется