а b c



Түзу шексіз. Сондықтан біз суретте түзудің бөлігін ғана сызып көрсете аламыз. Түзудің символы болып, ұшындағы нүктелері ерекшеленбей сызылған түзудің бөлігі алынады.
Үстелдің бетін , терезе әйнегінің бетін, тақтаның бетін жазықтықтар деп қарастыруға болады. Бірақ оларда жазықтықтардың бөліктері ғана, Кез-к елген жазықтықты барлық жағына шексіз созуға болады.
а
№1. Бір оқушы тақтаға орындайды.

а түзуін сызып оның бойына К, L, М нүктелерін белгілеңдер.Осы нүктелер арқылы түзуді белгілеп жазыңдар.

Шешуі:



K a, L a,M a
№ 6-сабақ: Кесінді. Кесіндінің ұзындығы

---

Мақсаты: Кесінді оның ұзындығын табуға арналған есептер шығаруға дағдыландыру. Кесіндінің геометриялық фигура екендігін және оны қандай әріптермен белгілейтінін үйрету. Біліктерін сараланған есептер шығару арқылы логикалық оймен іске асыра білу. 

Қысқаша мазмұны:

Екі нүктемен шектелген түзудің бөлігін кесінді деп атайды.Нүктелердің өзі кесіндінің басы және ұшы деп аталады.Кесіндіні өлшеу дегеніміз- оның ұзындықтарын табу.

Кесінді деген не? а түзуінде төрт A, B, C және D нүктелерін салайық:



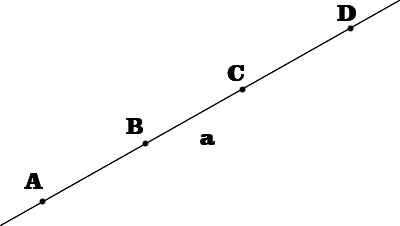
B  нүктесі  A  және  C нүктелерінің арасында жатыр. Ал  D нүктесі A және C нүктелерінің арасында жатпайды.

AC кесіндісі деп A және C нүктелерінің арасында жатқан барлық нүктелердің жиынтығын атаймыз. Бұндай нүктелер шексіз көп.A және C нүктелері кесіндінің ұштары деп аталады.

AС кесіндісің екі AB және BC кесінділеріне бөлуге болады. BC кесіндісі деген не? Бұны қалай түсінесіз? Жауабын түсіндіру.

Кесіндінің негізгі қасиеті

Түзуде жатқан үш нүктенің тек біреуі ғана қалған екеуінің арасында жатады.

Мысалы жоғарыдағы суреттегі A, B, C нүктелерінің тек біреуі ғана қалған екеуінің арасында жатыр, бұл B нүктесі:

№ 7- сабақтың тақырыбы: Сәуле. Бұрыш

Мақсаты: Сәулені, бұрыштың өлшем бірлігімен, бұрышты өлшейтін аспаппен және оны қолдану алгоритмімен таныстыру. Бұрыштарды өлшеу машықтарын қалыптастыру. Коммуникативтік машықтарды қалыптастыру, ұқыптылыққа тәрбиелеу.

Негізгі сұрақтар:

1. 
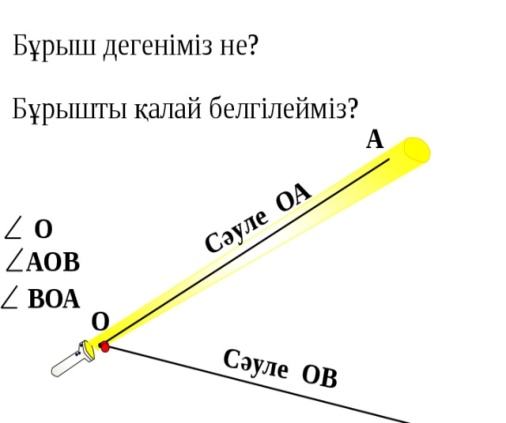
   Сәуле, сәуленің басы, толықтауыш сәулелер, сәуленің белгіленуі.
   
2. 
   Бұрыш, бұрыштың қабырғалары, төбелері, бұрыштың белгілену тәртібі, түрлері.
   

---

№8-9 сабақтың тақырыбы: Бұрыштың түрлері.

Мақсаты: Бұрыштардың түрлерін анықтауға, бір-бірінен ажыратуға дағдыландыру. Үшбұрышты сызғышты пайдаланып, тікбұрышты салуға дағдыландыру.

Қағаз бетіне бұрыш саламыз да, оны қиып аламыз. Бұрыш моделі бойынша оқушы бұрыштың төбелері мен қабырғаларын айтады.

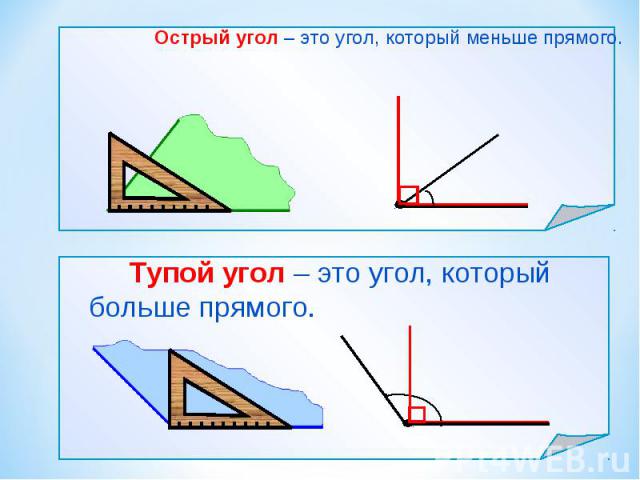
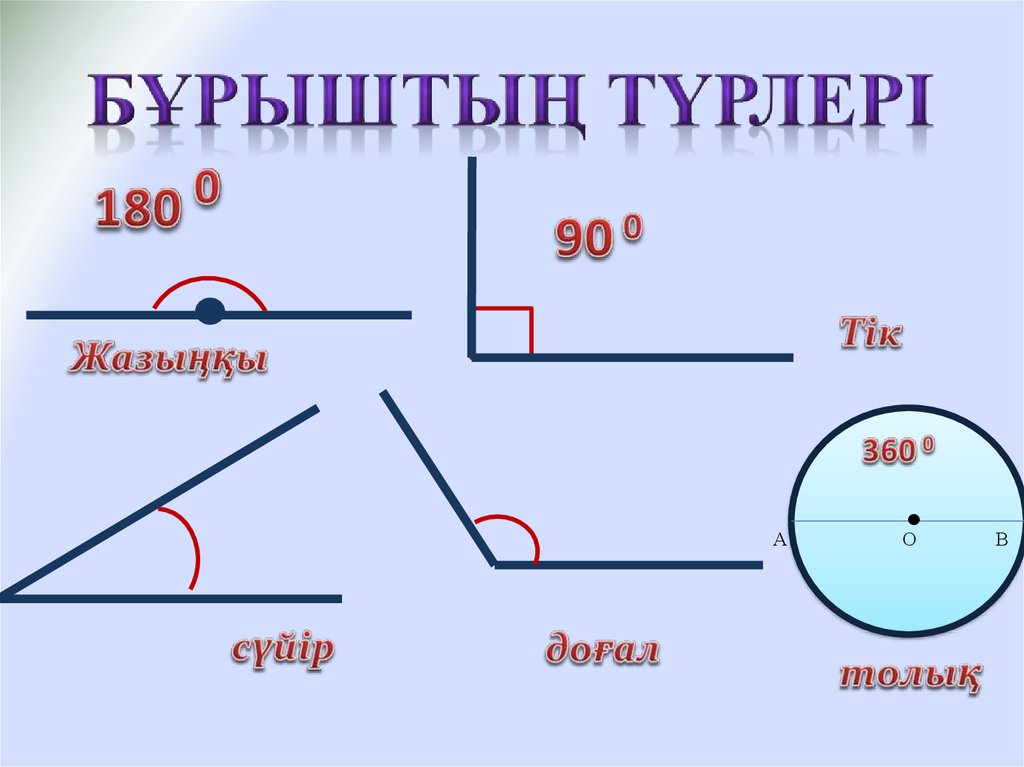
Тік бұрыштың градустық өлшемі 90⁰-қа тең.Тік бұрыштан кіші бұрыш сүйір бұрыш деп аталады. Тік бұрыштан үлкен, жазыңқы бұрыштан кіші бұрыш доғал бұрыш деп аталады.Қабырғалары түзу құрайтын бұрыштар жазыңқы бұрыш деп аталады. Жазыңқы бұрыш 180⁰-қа тең.

Бұрыш–бір  нүктеден шыққан әр түрлі екі сәуледен құралған геометриялық фигура. Сәулелер бұрыштың қабырғалары, ал олардың ортақ нүктесі бұрыштың төбесі деп аталады. Егер екі бұрыштың сәйкес қабырғалары  мен төбелерін беттестірген кезде дәл келсе, онда мұндай бұрыштар тең (конгруэнтті) бұрыштар делінеді. Егер екі бұрыштың төбесі мен бір қабырғасы ортақ болып, ал қалған екі қабырғасы түзу құраса, онда мұндай бұрыштар сыбайлас бұрыштар деп аталады. Жалпы айтқанда, төбесі мен бір қабырғасы ортақ бұрыштар іргелес (жапсарлас) бұрыштар делінеді. Егер бір бұрыштың қабырғалары бұрыш төбесінен бастап екінші бұрыштың қабырғаларының созындылары болса, онда ондай бұрыштар вертикаль бұрыштар деп аталады. Вертикаль бұрыштар өзара тең болады.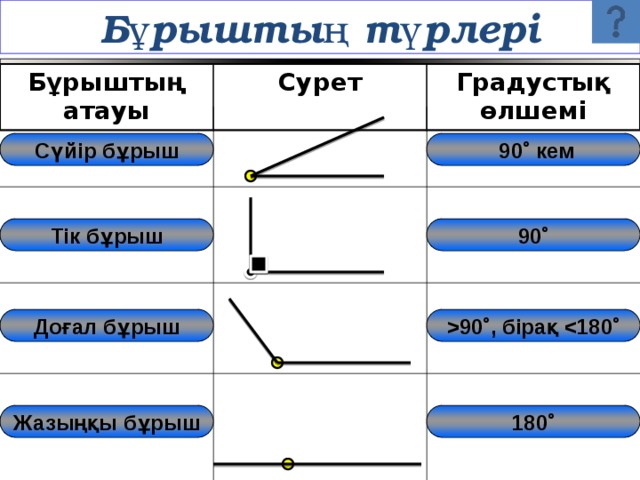

• 
  Егер бұрыштың қабырғалары түзу құраса онда мұндай бұрыш жазық бұрыш делінеді.
  
• 
  Өзінің сыбайлас бұрышына тең бұрыш тік бұрыш деп аталады.
  
• 
  Тік бұрыштан кіші бұрыш сүйір бұрыш,
  
• 
  Тік бұрыштан үлкен, жазық бұрыштан кіші бұрыш доғал бұрыш деп аталады.
  

№ 10-сабақтың тақырыбы: Бұрыштарды өлшеу. Транспортир.Үшбұрышты сызғыш.

Мақсаты: Бұрыштарды салыстыру бір-бірінен ажыратуға дағдыландыру.

Бұрыштарды өлшеу үшін транспортир қолданылады. Транспортир шкаласы жарты шеңбер бойына орналастырылған. Осы жарты шеңбердің центрі транспортирде кішкене сызықшамен белгіленген.

---

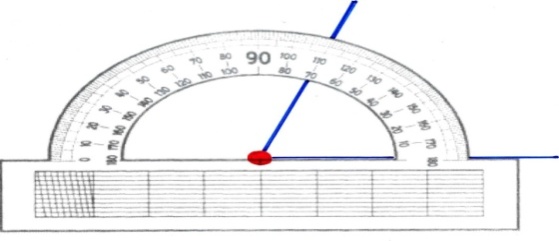
Транспортирдің сызықшалары ( штрихтары) жарты шеңберді 180 бөлікке бөледі. Осы жарты шеңбердің центрінен жүргізілген сәулелер әрқайсысы жазыңқы бұрыштың 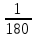бөлігіне тең 180 бұрыш жасайды. Мұндай бұрыштарды градустар деп атайды. Жазыңқы бұрыштың 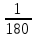бөлігіне тең бұрышты градус деп атайды. Градусты 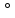таңбасымен белгілейді. Тең бұрыштардың градустық өлшеуіштері де тең болады, үлкен бұрыштың градустық өлшеуіші –үлкен , кіші бұрыштың градустық өлшеуіші кіші болады. Транспортирді бұрыштарды салу үшін де қолданады.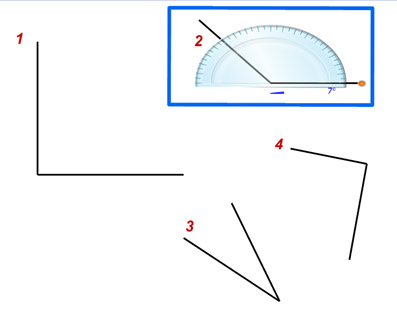



Бұрыштарды өлшеу алгоритмін енгіземіз (а суреті).

1. 
   Транспортирді центрі бұрыштың төбесі О нүктесімен сәйкес келетіндей етіп қоямыз.
   
2. 
   ОВ сәулесі нольдік белгіден (санақ басынан) өтеді.
   
3. 
   ОА сәулесі 60⁰ белгісінен өтіп тұр.
   
4. 
   Бұрыш АОВ=60⁰.
   

№11-сабақтың тақырыбы: Бұрыштарды салыстыру

Мақсаты: Бұрыштарды салыстыру тәсілдерімен оқушыларды таныстыру.

Жағымды психологиялық ахуал.

Егер екі бұрыштың градустық өлшемдері бірдей болса, онда бұл бұрыштарды тең бұрыштар деп атайды. Айналадағы заттардан бұрышты табу, шама бойынша бұрыштарды салыстыру. Балаларды бұрышпен бірге оның ішкі облысы жөнінде түсінік қалыптастыру үшін алғашқы кезеңдерде бұрыштардың қызық модельдерімен бірге «қозғалмалы бұрыш» моделі қолданылады. Әрбір оқушыға пластилин немесе шеге арқылы бекітілген екі таяқшадан тұратын осындай модель жасау тапсырылады. Осындай модель көмегімен бұрыштың өлшемі оның қабырғаларының ұзындықтарына тәуелді емес, қабырғалардың бір- біріне қатысты өзара орналасуына байланысты- қабырғалары неғұрлым жақын болса, бұрыш аз, ал қабырғалары арасы қашық болса, бұрыш үлкен болатынын байқайды.

№12 -сабақ: Сынық сызық

Мақсаты: Оқушыларға сынық сызық, көпбұрыш жайлы түсінік беру. Сынық сызықтың ұзындығын табу үшін оның буындарының ұзындықтарын қосу керектігін ұғындыру.

---

Егер сынықтың буындары өзара қиылыспайтын болса, ол жай сынық деп аталады. Сынық сызықтың ұзындығын табу үшін оның буындарының ұзындықтарын қосу керек. Сынықтың ұзындығы оның ұштарын қосатын кесіндінің ұзындығынан кем болмайды.

Көпбұрыш – кез-келген тұйық сынық сызық. Сынық сызықтың әр бөлігі – қабырға, әр ұшы- төбесі болады. Көпбұрыштың барлық қабырғасының қосындысы оның периметрі болады. Егер сынық сызық қарапайым болса, онда көпбұрыш қарапайым көпбұрыш деп, ал күрделі болса, жұлдыз тәрізді көпбұрыш деп аталады. Көпбұрыш жазықтықты бірнеше облысқа бөледі. Қарапайым көпбұрыш жазықтықты біреуінде түзу толығынан жататын, ал екіншісінде толық жатпайтын екі облысқа бөледі. Біріншісін көпбұрыштың сыртқы облысы, екіншісін ішкі облысы дейді. Көпбұрыш осы облыстардың шекарасы болады. Көпбұрыш пен оның ішкі облысын біріктірсек, екі өлшемді көпбұрыш шығады. Егер көпбұрыштың төбелері кез келген қабырғасы арқылы жүргізілген түзудің бір жағында жатса, онда оны дөңес көпбұрыш дейді. Төбесі арқылы өтетін қабырғалардың ішкі облыс жағынан жасайтын бұрышын көпбұрыштың ішкі бұрышы дейді. Көпбұрыштардың атауы олардың қабырғаларының санына байланысты болады.Мысалы, бесбұрышта – бес, ал алтыбұрышта алты қабырға бар. Үлкен сандағы қабырғалары бар көпбұрыштар біршама сирек кездеседі. Олардың атаулары ұзақ, мысалы, онбірбұрыш, онүшбұрыш. Көпбұрыштың қабырғалары неғұрлым көп болса, ол соғұрлым шеңберге көбірек ұқсайды. Анықтамалардың біріне сәйкес, шеңбер дегеніміз – сансыз көп қабырғалары бар көпбұрыш.

Көпбұрыштар табиғатта біршама сирек кездеседі. Дегенмен сендер олардың кейбіреуін көруің мүмкін. Алманы қақ ортасынан кесіп бөл де, дәндеріне қара. Олар бесбұрыш құрайды. Теңіз жұлдызы мен теңіз кірпісінің денелері бес бөліктен тұрады, оларды шеңберге жатқызуға болады.


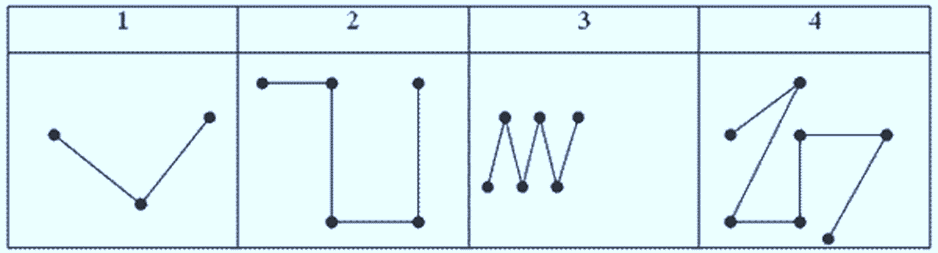
Сынықтың ұзындығын табу үшін...

Буындарының ұзындықтарын қосу керек



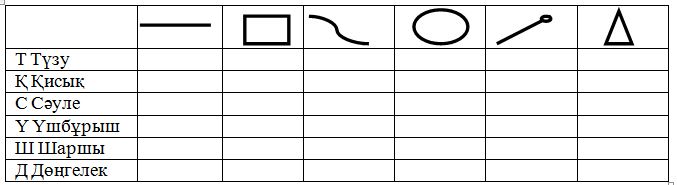
№13-сабақтың тақырыбы: Көпбұрыш.

Мақсаты: Оқушыларға сынық сызық, көпбұрыш жайлы түсінік беру Сынық сызықтың ұзындығын табу үшін оның буындарының ұзындықтарын қосу керектігін ұғындыру.

Көпбұрыштың атауы қабырғаларының санына байланысты болады. Мысалы, бес бұрышта бес, ал алты бұрышта алты қабырға бар. Көпбұрыштың қабырғалары неғұрлым көп болса, соғұрлым шеңберге ұқсайды.

---

Смотрите также файлы

• Отчет по итогам 20202021 учебного года.docx

• Контрольная работа 2 По обществознанию за i полугодие 1.doc

• Практическая работа 4 Изучение строения Солнца, его атмосферы и влияние солнечной активности на Землю Цель работы.docx

• Дисциплина Экономическаятеория.docx

• Задания на формирование предметных результатов.docx