Сызбаны аяқта. Жайылмалы алты бұрыш жаса


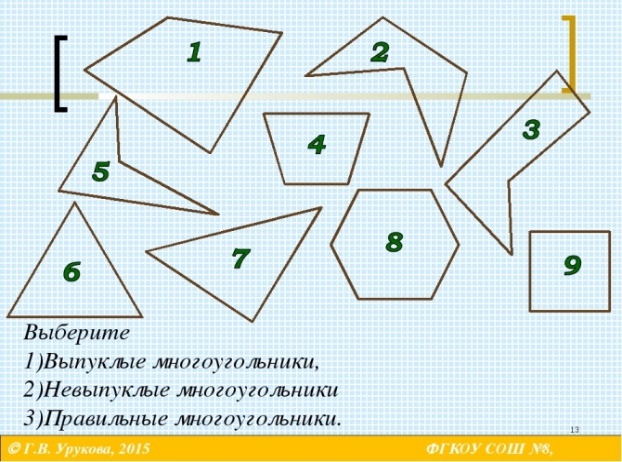
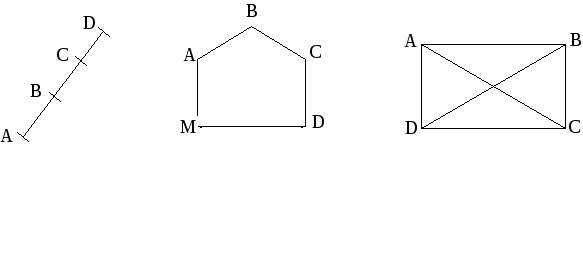
Көпбұрыштың элементтерін бөліп көрсете отырып, оқушылар көпбұрыштардың қабырғалары кесінділер екенін тағайындайды. Кесінділерді бөліп көрсетуге берілген жаттығуларды, олрға оқушылардың шамасы келетіндей болу үшін, біртіндеп күрделендіру қажет. Мысалы, балалар көре және көрсете білуі үшін оларды мынадай жеңілірек тапсырмалар орындауға үйретк керек.Оқушылар екішші сыныпта кесінділерді әріптермен белгілеумен танысқанда жазбаша жаттығулар беріледі, бұл жаттығулар басқа бір кесіндінің бөлігі болып табылатын кесінділерді, сондай – ақ басқа кесінділерден тұратын кесінділерді бөліп көрсете білуді пысықтайды. Мысалы, барлық кесінділерді жазып көрсету, болса Онүктесінде жатқан кесінділерді жазып көрсету, тең кесінділердің сызғыштың көмегімен өлшеу және жазып көрсету ұсынады. 

Біртіндеп оқушылар кесінді бірнеше көпбұрыштың ортақ қабыррасы бола алатан түсінеді, осыған сүйеніп II және III сыныптарда , жаңа фигура пайда болатындай етіп, көпбұрыштардың ішіне кесінділер салу жаттығуларын орындайды; мысалы, бесбұрыштың ішінен кесінді жүргізу керек, ол кесіндінің бойымен қиғанда үшбұрыш және төртбұрыш немесе екі төртбұрыш, үшбұрыш және алтыбұрыш шығатын болсын. Оқушылар тапсырмаларды дәптерлеріне жазады, содан кейін әр есептің түрлі шешуі анықталып, тақтада көрсетіледі.



№ 14-15 сабақтың тақырыбы: Фигураларды салу есептері

Мақсаты: Оқушыларға салу есептерінің қыр-сырын меңгерту:

Ең қарапайым салу есептері өте ерте заманда жер танаптарын өлшеу және әр түрлі құрылыстарды салу жұмыстарын орындағанда пайда болған. Алғашқы мұндай есептер тобына мынадай есептер жатады: берілген кесіндіге тең кесінді салу, кесінділерді және бұрыштарды тең екі бөлікке бөлу, берілген нүкте арқылы берілген түзуге перпендикуляр жүргізу. Бұл есептердің шешуі гректерден бұрынғы дәуірдің өзінде-ақ белгілі болатын.

Біздің эрамызға дейінгі VII ғасырдан III ғасырға дейінгі уақыт аралығында грек ғалымдары геометрия саласында

---

, жекелеп айтқанда салу есептері жөнінде аса көп материал жинап, оларды өңдеді.Бұл жерде бір жағдайды атап ескерту қажет: салу жұмысын орындағанда тек сызғыш пен циркуль пайдаланып, басқа аспаптар қолданылмағанда ғана мұндай салуды ежелгі грек ғалымдары геометриялық салу деп есептеген. Ал егер салу жұмысын орындағанда басқа аспаптар, мысалы чертеждік үшбұрыш, бөліктері бар сызғыш қолданылса, онда мұндай шешуді геометриялық шешу деп есептемеген.

Ерте заманнан бізге келіп жеткен деректерге қарағанда, б.э. дейінгі VI ғасырда өмір сүрген Пифагордың өзі дұрыс бесбұрышты және онбұрышты салу тәсілдерін жіне кейбір күрделірек салу есептерін тапқан. Салу есептерін шешу тәсілдерін жасау ісіне Платон (б.э. дейінгі V ғасыр) және оның шәкірттері үлкен үлес қосқан. Платон заманынан бері салу есептерін шешудің мынадай төрт кезеңі ажыратылып қарастырылатын болды: 1) анализ (талдау), 2) салуды орындау, 3) дәлелдеу және 4) зерттеу.

Кесіндіні қақ бөлудің біздің оқулықтарда көрсетілген тәсілі Прокл (410-485ж.) комментариінде баяндалған, оның пікірінше, бұл тәсілді атақты грек математигі Аполлоний (б.э. дейінгі III ғасыр) тапқан.



Е вклидтің атақты «Бастамаларында» салу есептерін қарастыруға үлкен орын берілген.Евклид қандай да бір фигураның бар болатындығын дәлелдей отырып, ол фигураны тек сызғыш пен циркульды қолданып қалай салуға болатындығын көрсетіп отырған. Оның 13 кітабында көптеген салу есептері қарастырылған.

Евклид«Бастамаларының» бірінші кітабында үшбұрыштарды салу тақырыбы енгізілген. Оның төртінші кітабында басқа мәселелермен бірге, дұрыс төртбұрыштарды, бесбұрышты, алтыбұрышты және он бес бұрышты салу мәселелері қарастырылған. Әсіресе бұрышты тең үш бөлікке бөлу (бұрыш трисекциясы) туралы есепке көп еңбек сарп болған.Алайда бұл есепті шешуге арналған барлық еңбек зая кетті. Бұл есепті тек сызғыш пен циркульді қолданып шешуге болмайтындығы қазіргі уақытта дәлелденді.

Тапсырма ретінде ұсыну: төртбұрыш сызу. Оның төбелері мен қабырғаларын көрсету. Диагональдарын жүргізу. Өзара бірдей екі сүйір бұрыш сызу. Тік бұрыш салу және оның бұрышын белгілеп көрсету.

---

№16-сабақ: Шеңбер және дөңгелек

Мақсаты: Шеңбер және дөңгелек,олардың бөліктері туралы түсінік беру

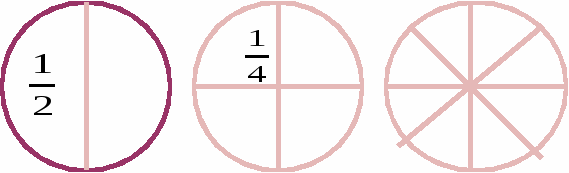
Дәптерге О нүктесін белгілеп және одан бірдей ұзындықтағы кесінділер сызып, О нүктесінен бірдей қашықтықтағы нүктелерді аламыз. Егер барлығын осындай нүктелермен белгілесек, шеңбер аламыз. Мұні циркульдың көмегімен жасауға болады. Шеңбердің кез келген нүктесін шеңбердің центрімен қосатын кесіндіні радиус деп атайды. Шеңбердің центрі арқылы өтетін және шеңбердің екі нүктесін қосатын кесіндіні диаметр дейміз. Егер шеңбер бойымен қағаздан фигураны қырқып аланған қағазды дөңгелекдейміз. Шеңбер тек дөңгелектің шекарасы ғана

Берілген шеңберлерді бөлшекте және боя


1. Шеңбер дегеніміз не?

2. Шеңбердің диаметрі дегеніміз не?

3. Шеңбер мен дөңгелектің қандай ерекшелігі бар?

№17- сабақтың тақырыбы: Тік төртбұрыш.Тік төртбұрыштың ауданы.

Мақсаты: Тік төртбұрыш оның ауданын табуға берілген есептер шығару,тіктөртбұрыштың ауданын табу ережесімен таныстыру.

Төртбұрыш деп үш нүктесі бір түзудің бойында жатпайтын төрт нүктеден және оларды қосатын кесінділерден тұратын тұйық фигураны атайды.Мысалы.



 Тік төртбұрыш деп барлық бұрыштары тік (90⁰ градусқа тең) болатын төртбұрыштарды атаймыз:



Тік төртбұрыштың ауданын табу үшін, оның ұзындығын еніне көбейту керек. Тік төртбұрыштың ауданын S әрпімен, ұзындығын а әрпімен , енін b әрпімен белгілейік. Сонда тік төртбұрыштың ауданының формуласы мынадай болады: S=ab

№18- сабақтың тақырыбы: Шаршы. Шаршының ауданы.

Мақсаты: шаршының ауданын табу ережесімен таныстыру.

Шаршы – барлық қабырғалары тең тік төртбұрыш.Шаршының ең жақын тегі – тік төртбұрыш.Шаршының ұзындығы мен ені тең, оның ауданын мына формула бойынша есептейді: S=a

---

^.а

 Егер шаршының қабырғасының ұзындығы а-ға тең болса, онда оның ауданы  а²-қа тең болады.

№19-20 сабақтың тақырыбы: Үшбұрыш.Үшбұрыштың элементтері.

---

Мақсаты: Оқушыларды үшбұрыш фигурасымен таныстыру.

Үшбұрыш – ең қарапайым түзу сызықты тұйық фигура, ол – қасиеттерін адам өте ерте кездің өзінде-ақ танып білген фигуралардың бірі, өйткені бұл фигура практикалық өмірде әрдайым кеңінен қолданылып отырған. Әр түрлі құрылыс бөліктерін және олардың детальдарын бір-біріне берік бекіту үшін құрылыс өнерінде үшбұрыштың қатаңдық қасиеті атам заманнан бері үнемі қолданылып келеді. Үшбұрыштардың кескіндері және үшбұрышқа берілген есептер папирустарда, үнділердің ескілікті кітаптарында және басқа да документтерде кездеседі. Ежелгі Грецияда үшбұрыштар жөніндегі ілім б.э. дейінгі VII ғасырда Фалес ұйымдастырған иониялық мектепте және Пифагор мектебінде дамыды.Үшбұрыш бір қабырғасы және онымен іргелес екі бұрышы арқылы анықталатынын Фалес сол кезде-ақ дәлелдеген болатын. Мұнан кейін үшбұрыштар жөніндегі ілім Евклид «Бастамаларының» бірінші кітабында толық баяндалды. Бұл кітаптың беташарында келтірілген «анықтамалардың» ішінде мынадай анықтамалар да берілген: «Үш қабырғалы фигуралар ішіндегі тең қабырғалы үшбұрыш дегеніміз тең үш қабырғасы бар фигура, тең бүйірлі дегеніміз – тек екі қабырғасы тең фигура, әр қабырғалы дегеніміз – тең емес үш қабырғасы бар фигура. Үшбұрыш туралы ұғым тарихы, сірә, былайша дамыған болар: әуелі тек дұрыс үшбұрыштар, сонан кейін тең бүйірлі үшбұрыштар, ең ақырында әр қабырғалы үшбұрыштар қарастырылған.


Үшбұрыштың элементтері

Мақсаты: Үшбұрыштың элементтерімен оқушыларды таныстыру

Үшбұрыштың үш төбесі, үш қабырғасы, үш бұрышы бар екен. Олар үшбұрыштың элементтері деп аталады. ВС=а, СА=в, АВ=с.Үшбұрыштың бұрышы деп аталады.

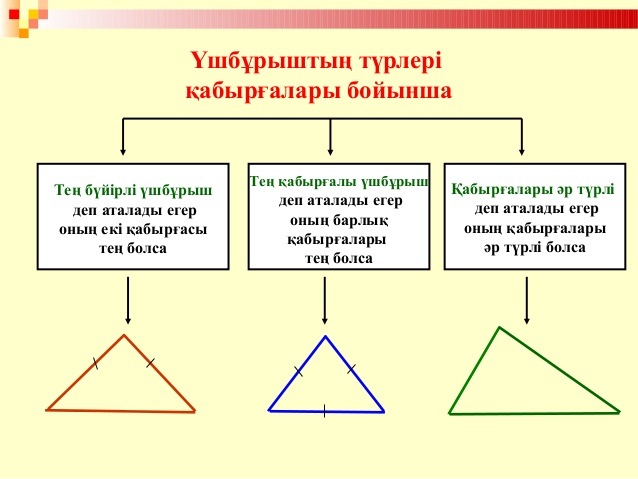
Үшбұрыш қабырғаларының үзындықтарына байланысты –үш топқа бөлінеді.

Олар: 1.Қабырғаларының ұзындықтары әр түрлі болатын әр түрлі қабырғалы үшбұрыш;

2.Екі қабырғасы тең болатын теңбүйірлі үшбұрыш

( өзара тең екі қабырғасы оның бүйір қабырғалары, ал үшіншісі – табаны деп аталады)

Үш қабырғасы тең болатын теңқабырғалы үшбұрыш деп аталады.

---

Смотрите также файлы

• Отчет по итогам 20202021 учебного года.docx

• Контрольная работа 2 По обществознанию за i полугодие 1.doc

• Практическая работа 4 Изучение строения Солнца, его атмосферы и влияние солнечной активности на Землю Цель работы.docx

• Дисциплина Экономическаятеория.docx

• Задания на формирование предметных результатов.docx