---

КОНТРОЛЬНЫЕ ВОПРОСЫ

3. 
   Чем дискретные случайные величины отличаются от непрерывных?
   
4. 
   Перечислите способы задания дискретной случайной величины.
   

ЛИТЕРАТУРА

1. 
   Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007.
   

Практическая работа №7

РЕШЕНИЕ ЗАДАЧ НА ЗАПИСЬ РАСПРЕДЕЛЕНИЙ

ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
ЦЕЛЬ РАБОТЫ: научиться строить биноминальные и геометрические распределения дискретных случайных величин.

Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять вероятность событий с использованием элементов комбинаторики.

Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетной документации, принимать участие в разработке проектной документации на модификацию информационной системы; ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

1. 
   Биноминальное распределение имеет место, когда производится n независимых испытаний, в каждом из которых событие может либо появится, либо не появиться.
   

Вероятность наступления события во всех испытаниях постоянна и равна р, следовательно вероятность ненаступления равна q = 1 - р.

Биноминальным распределение определяется формулой Бернулли:



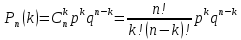
Пример 1.Построить закон распределения случайной величины Х – количества домов, данных в эксплуатацию в срок, из 3 строящихся. Вероятность сдачи в эксплуатацию в срок для каждого дома одинакова и равна 0,9.

Решение

---

1. 
   Возможные значения случайной величины Х: х₀=0, х₁=1, х₂=2 или х₃=3.
   
2. 
   Число испытаний (общее число строящихся домов):n= 3.
   

Вероятность наступления события A в одном опыте (построить каждый дом в срок)

p = 0,9.

3. 
   Вероятности возможных значений p_i: определяем с помощью формулы Бернулли:
   

р₀ = Р(х=0) = р₃(0) = С₃⁰р⁰q³= 1*0,9⁰*0,1³ = 0,001

p₁ = Р(х=1) = р₃(1) = С₃¹р¹q²= 3*0,9¹*0,1²= 0,027;

p₂ = Р(х=2) = р₃(2) = С₃²р²q¹= 3*0,9²*0,1¹= 0,243;

p₃ = Р(х=3) = р₃(3) = С₃³р³q⁰= 1*0,9³*0,1⁰= 0,729.

Полученные значения помогают сформировать ряд распределения.

Х	0	1	2	3
р	0,001	0,027	0,243	0,729

2. 
   Распределение Пуассона – имеет место, когда производится большое количество испытаний, но вероятность появления события мала.
   

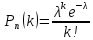, где  = np.

Пример 2. Завод отправил на базу 4000 доброкачественных изделий. Вероятность того, что в пути изделие проверится, равно 0,0002. Найти закон распределения числа проверенных изделий (при подсчете используйте таблицу распределения Пуассона). Вариантов случайной величины Х – числа проверенных изделий должно быть столько, чтобы сумма их вероятностей была близка к 1.

Решение

1. 
    = np = 4000*0,0002 = 0,8
   
2. 
   Возможные значения случайной величины Х:
   

х₀=0, х₁=1, х₂=2, х₃=3, х₄ = 4 и т.д. до х₄₀₀₀ = 4000.

3. 
   По таблице распределения Пуассона получим:
   

P(x=0) = 0,449329

P(x=1) = 0,359463

P(x=2) = 0,143785

P(x=3) = 0,038343

P(x=4) = 0,007669

P(x=5) = 0,001227

4. 
   Закон распределения:
   

Х	0	1	2	3	4	5	…	4000
Р	0,449329	0,359463	0,143785	0,038343	0,007669	0,001227	…	0

---

 0,999816  1

3. 
   Геометрическое распределение – имеет место, когда производятся независимые испытания, в каждом из которых вероятность появления события равна р. Испытания заканчиваются, как только появляется событие А.
   

Пример 3. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдаются патроны до тех пор, пока он не попадет. Требуется составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку.

Решение

1. 
   Возможные значения случайной величины Х: х₁= 1, х₂ = 2, х₃ = 3, … х_k=k и т.д.
   
2. 
   Вероятности возможных значений:
   

p₁ = p = 0,8

p₂ = qp = 0,8*0,2 = 0,16

p₃ = q²p = 0,8*0,2² = 0,032 и т.д.

p_k = q^kp = 0,8*0,2^k-1

Х	1	2	3	…	k	…
р	0,8	0,16	0,032	…	0,8*0,2k-1	…

4. Гипергеометрическое распределение

Рассмотрим задачу. Пусть в партии из Nизделий имеется М стандартных. Из партии случайно отбирают n изделий с одинаковой вероятностью, причем отобранное изделие не возвращают обратно (поэтому формула Бернулли не работает). Найти вероятность, что среди nотобранных изделий ровно m стандартных.


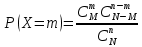
Пример 4. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.

Решение

N = 10 – число деталей в партии;

M = 8 – число стандартных деталей;

n = 2 – числоотобранных деталей;

m – число стандартных деталей среди отобранных.

1. 
   Возможные значения случайной величины Х – числа стандартных деталей среди отобранных деталей: х₁ = 0, х₂ = 1, х₃ = 2.
   
2. 
   Вероятности возможных значений:
   

Р₀(х=0) =

---

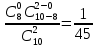
Р₁(х=1) =
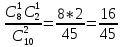
Р₂(х=1) =

3. 
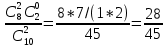
   Закон распределения:
   

Х	0	1	2
Р	1/45	16/45	28/45

ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ

	I вариант	II вариант
1.	Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Чему равна вероятность, что откажет менее двух приборов в опыте? Построить многоугольник распределения.	По мишени проводится три выстрела с вероятностью попадания 0,8. Найти закон распределения случайной величины Х – число попаданий в мишень. Чему равна вероятность, что произведено более одного попадания? Построить многоугольник распределения.
2.	Учебник издан тиражом 10000 экземпляров.Вероятность того, что учебник сброшюрован неправильно,равна 0,0001. Найти закон распределения числа бракованных книг (при подсчете используйте таблицу распределения Пуассона) Вариантов случайной величины Х - количества бракованных книг должно быть столько, чтобы сумма их вероятностей была близка к 1.	Устройство состоит из 1000 элементов, работающихнезависимо один от другого. Вероятность отказалюбого элемента в течение определенного времени равна 0,002. Найтизакон распределения числа отказавших элементов (при подсчете используйте таблицу распределения Пуассона) Вариантов случайной величины Х – числа отказавших элементов должно быть столько, чтобы сумма их вероятностей была близка к 1.
3.	Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р = 0,6.Требуется: а) составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.	Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р = 0,9.Требуется: а) составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.
4.	В партии из семи деталей имеется три стандартных. Наудачу отобраны три детали. составить закон распределения дискретной случайной величины Х – числа стандартных деталей среди отобранных. найти наивероятнейшее число стандартных деталей среди отобранных.	В партии из восьми деталей имеется пять стандартных. Наудачу отобраны три детали. составить закон распределения дискретной случайной величины Х – числа стандартных деталей среди отобранных. найти наивероятнейшее число стандартных деталей среди отобранных.

---

Смотрите также файлы

• перпендикулярные прямые.docx

• Разработка урока в рамках формирования универсальных учебных действий (на примере темы Буквы Ш,ш, обозначающие согласный звук (ш, ) по учебному предмету русский язык (обучение грамоте).docx

• Добрый вечер, Алексей!.pdf

• Занятие для обучающихся 89 классов по теме день конституции.pdf

• Теоретические основы доступа информации как проблема региональной журналистики 5.doc