Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.01.2024

Просмотров: 1008

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


xi
2
3
4
5

ni
14
19
5
2

Wi
0,35
0,475
0,125
0,05

Si
0,35
0,825
0,95
1

г) Построим полигон частот, отложив по оси абсцисс значения xi, а по оси ординат - ni. Аналогично построим полигон относительных частот.

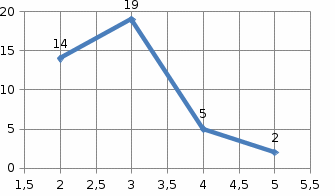
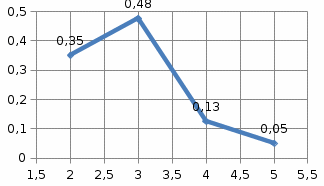
Пример 2. На школьниках 1-го «А» класса было проведено исследование для выяснения того, сколько весит портфель первоклассника. В результате взвешиваний был получен следующий статистический ряд (масса каждого портфеля в кг): 2,1; 2,45; 1,9; 2,6; 3,1; 1,95; 3,4; 4,3; 1,15; 2,7; 2,2; 3,2; 2,4; 2,2; 1,8; 1,5; 2,4; 2,25; 2,6; 1,75.

а) постройте статистический ряд в виде интервальной таблицы частот, определите относительные частоты на каждом интервале.

б) постройте гистограмму частот и относительных частот.
Решение

а) Для построения статистического ряда данных в виде интервальной таблицы частот разобьем все значения выборки на равные промежутки по 1 кг и подсчитаем число попаданий в каждый из них. Для нахождения относительных частот используем формулу: Wi = ni/n. В нашем примере n = 20.

xi
1-2
2-3
3-4
4-5

ni
6
10
3
1

Wi
0,3
0,5
0,15
0,05


б) Для построения гистограммы частот определим для каждого интервала его длину h и плотность частоты (ni/h).

h = 1 (определяется как разность xi интервала); n1/h=6/1=6; n2/h=10/1=10; n3/h=3/1=3; n4/h=1/1=1.


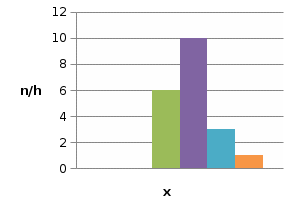
1
2
3
5
4

Аналогично строится гистограмма относительных частот.


ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ

I вариант

Задание 1. Дан числовой ряд, представляющий итоговые оценки по математике студентов 1 курса:

3 4 5 4 4 3 5 4 4 3 5 4 5 3 3 4 4 4 5 3 3 5 5 4 5.

а) построить для него вариационный ряд; б) построить статистическое распределение для частот и относительных частот; в) дополнить статистическое распределение накопленными частотами;

г) построить полигон частот и относительных частот.
Задание 2. В отделе мужской обуви универмага в течение дня производился учет стоимости проданной обуви. Были получены следующие результаты (в рублях):

1200, 1110, 2300, 890, 320, 1200, 560, 1340, 1400, 1050, 1050, 4700, 3200, 2900, 2100, 2450, 890, 1110, 1200, 1200, 2300, 1050, 1400, 1200, 890, 320, 1320, 890, 1100, 1050

а) Представьте эти данные в виде интервальной таблицы абсолютных и относительных частот, разбив диапазон цен от 0 до 5000 рублей на интервалы длиной по 1000 рублей.

б) постройте гистограмму частот и относительных частот.
II вариант

Задание 1. Дана случайная выборка из 25-ти учеников 8-го класса с данными об их росте: 166 165 163 166 168 165 168 170 165 165 165 165 164 168 165 164 161 166 166 167 164 163 168 167 167.

а) построить для него вариационный ряд; б) построить статистическое распределение для частот и относительных частот; в) дополнить статистическое распределение накопленными частотами;

г) построить полигон частот и относительных частот.
Задание 2. Перед вами выборка, полученная по результатам изучения обменного курса доллара в 20-ти обменных пунктах города: 26,45; 26,4; 26,41; 26,45; 26,66; 26,53; 26,55; 26,44; 26,8; 26,67; 26,77; 26,43; 26,7; 26,6; 26,68; 26,58; 26,55; 26,54; 26,57; 26,59

а) Разбейте весь интервал от 26,4 до 26,9 на пять интервалов, сгруппируйте данные и постройте по ним интервальную таблицу частот.

б) постройте гистограмму частот и относительных частот.

КОНТРОЛЬНЫЕ ВОПРОСЫ


  1. В чем суть выборочного метода? Чем отличается выборочная совокупность от генеральной?

ЛИТЕРАТУРА

  1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.

Практическая работа №13

ОПРЕДЕЛЕНИЕ ЧИСЛОВЫХ ХАРАКТЕРИСТИК ВЫБОРКИ.

ВЫЧИСЛЕНИЕ ТОЧЕЧНОЙ ОЦЕНКИ
Цель работы: научиться определять числовые характеристики выборок и определять точечные оценки.

Для выполнения работы необходимо знать виды числовых характеристик выборок и формулы для их определения, виды точечных оценок; необходимо уметь определять числовые характеристики выборок и точечные оценки.

Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Пусть выборка задана в виде таблицы частот.

xi
x1
x2
…
xk

ni
n1
n1
…
nk

Wi
W1
W2
…
Wk

Для нахождения числовых характеристик используются следующие формулы:

  1. Среднее: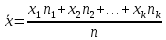 . Для интервальной таблицы в качестве варианты х берется середина интервала.

  2. Мода (модальный интервал) – значение варианты х с большей частотой.

  3. Медиана – значение варианты х, находящейся в середине ряда.

    1. Если вариационный ряд содержит нечетное количество чисел, то нужно взять число, которое находится ровно посередине. Если же ряд содержит четное количество чисел, то нужно взять два средних числа и найти их полусумму.

    2. При нахождении медианы по таблице частот нужно найти первое значение накопленной частоты, превосходящее 0,5, и выбрать соответствующее ему значение числового ряда. Если ряд имеет четное число слагаемых, тогда ровно посредине вариационного ряда будут находиться два значения: то, для которого накопленная частота равна 0,5, и следующее за ним. Для вычисления медианы нужно взять их полусумму.

    3. Для вычисления медианы по интервальной таблице частот используют пропорциональное деление отрезка, на котором происходит «перевал» накопленной частоты через 0,5.

Если границы интервала обозначить за хнач и хкон, накопленные частоты на этих границах за Sнач и Sкон , то медиана d вычисляется по формуле:



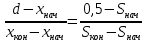
  1. Дисперсия: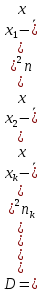 или D = 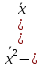. Для интервальной таблицы в качестве варианты х берется середина интервала.



  1. Среднее квадратическое отклонение: .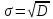

Точечной называется статистическая оценка, которая определяется одним числом Θ* = f(x1, x2, … xn), где x1, x2, … xn – результаты n наблюдений над признаком Х.

    1. Несмещенной называется точечная оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

    2. Смещенной называется точечная оценка, математическое ожидание которой не равно оцениваемому параметру.

Несмещенной оценкой генеральной средней является выборочная средняя:



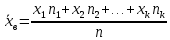
Смещенной оценкой генеральной дисперсии является выборочная дисперсия:



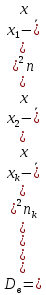
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия:


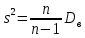
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
I вариант


  1. Для выборки 7; 3; 3; 6; 4; 5; 1; 2; 1; 3 определить среднее, моду и медиану.



  1. Дано статистическое распределение выборки:

xi
0,1
0,5
0,6
0,8

ni
5
15
20
10

Определить среднее, моду, медиану, дисперсию и среднее квадратическое отклонение.

  1. В таблице приведены результаты измерения роста случайно отобранных 100 студентов:

Рост

154-158
158-162
162-166
166-170
170-174
174-178
178-182

Число студентов
10
14
26
28
12
8
2

Определите среднее, моду, медиану и дисперсию роста обследованных студентов.


  1. Из генеральной совокупности извлечена выборка объемом n = 50. Найти несмещенную оценку генеральной средней.

xi
2
5
7
10

ni
16
12
8
14



  1. По выборке объема n = 51 найдена смещенная оценка Dв = 5 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.


II вариант


  1. Для выборки 1; 2; 3; 4; 5; 5; 9; 6; 4 определить среднее, моду и медиану.



  1. Дано статистическое распределение выборки:

xi
18,4
18,6
19,3
19,6

ni
5
10
20
15

Определить среднее, моду, медиану, дисперсию и среднее квадратическое отклонение.


  1. В таблице приведены данные о росте участников легкоатлетических соревнований:

Рост

160-165
165-170
170-175
175-180
180-185
185-190

Число участников
5
12
19
25
10
7

Определите среднее, моду, медиану и дисперсию роста обследованных студентов.


  1. Из генеральной совокупности извлечена выборка объемом n = 60. Найти несмещенную оценку генеральной средней.

xi
1
3
6
26

ni
8
40
10
2

Смотрите также файлы