Файл: Вдовин Суркова Валентинов Теория систем и системный анализ.pdf

240

Рис. 2.11. Таблица исходных и расчетных данных



241

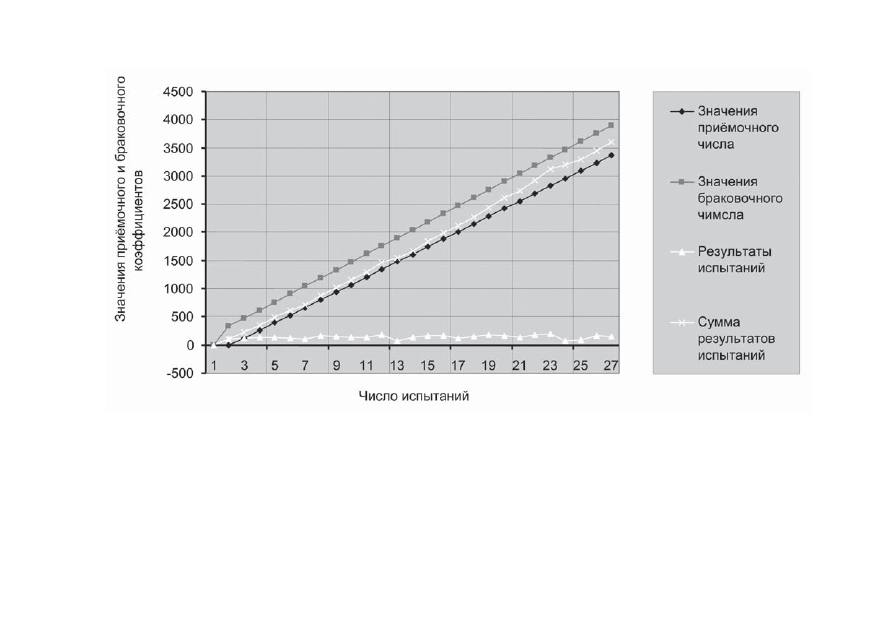
Рис. 2.12. Экспертиза системы по среднему значению выбранного параметра

242

8.2.4. Экспертиза качества системы по дисперсии выбранного 
параметра

Подобная задача возникает в тех случаях, когда про-

цессы, необходимо оценивать по среднему квадратическому 
отклонению 

  выбранного параметра х (известного или не-

известного)  от его среднего значения 

. Так, если качество 

продукции (процесса) считается тем выше, чем меньше 

 

то можно определить такую величину 

´,что изделие будет 

считаться нестандартным, если 

´ и удовлетворительным 

(отвечающим техническим требованиям), если 

´. Так как  

неизвестно, то задача состоит в определении способа проверки 
гипотезы, что 

´.

 Математическая формулировка задачи. Имеется случайная 

величина х, распределенная по нормальному закону. Требуется 
проверить гипотезу о том, что 

´ при условии, что вероятность 

классифицировать исследуемую партию изделий как неудо-
влетворительную не должна превышать величины 

, когда 

0

, 

а вероятность признать партию доброкачественной не должна 
превышать заданной величины 

, когда 



. Допускаемый риск 

определяется числами 

















 и .

Методика оценки качества системы по дисперсии выбран-

ного параметра.

1. Рассчитываются значения приемочного и браковочного 

чисел:

2

1

0

2

2

0

2

1

2

1

2

0

m

1

1

ln

m

1

1

1

ln

2

a

V

V

V

V

V

V

D

E

;

2

1

0

2

2

0

2

1

2

1

2

0

m

1

1

ln

m

1

1

1

ln

2

r

V

V

V

V

V

V

D

E

.

243

2. Проверяются условия и принимается решение о преиму-

ществе одной системы над другой:

• на m-м испытании вычисляется сумма 

¦

T

m

1

i

2

i

)

x

(

;

•проверяется условие 

¦

m

r

m

m

a

,

если 

m 

m

 — принимается гипотеза Н

0

;

если 

m r

m

 — принимается гипотеза Н

1

.

Пример. Проверить, удовлетворяет ли принимаемая пар-

тия промышленной продукции (контрольно-измерительные 
приборы) требованиям в отношении точности измерения за-
данного параметра. Предельные значения средних квадра-
тических отклонений ошибок измерения этих параметров 
и допустимые риски в приемке партии составляют



0

 = 1 м, 



1

 = 2 м, 

 =  = 0,05. Задачу решим в редакторе “Excel”.

Решение.
1. Подготавливается и заполняется таблица (рис. 2.13).
2. Строится график (рис. 2.14).
3. Делается вывод о приемке партии промышленной про-

дукции. Для условий данного примера партия промышленной 
продукции принимается.

8.3. Методы экспертных оценок, 

используемые при проведении

 сложных экспертиз

Теория экспертных оценок строится на различных методах 

организации работы специалистов-экспертов. 

Основными методами организации сложных экспертиз 

являются:

•метод парных сравнений;

•метод ранжировки мнений;

•метод шкальных оценок.

244

Рис. 2.13. Таблица исходных и расчетных данных