Файл: Вдовин Суркова Валентинов Теория систем и системный анализ.pdf
Добавлен: 12.02.2019
Просмотров: 22680
Скачиваний: 342
394
395
Таблица 3.4
x
1
x
2
x
3
x
4
x
i
10
20
15
30
i
ɯ
V
2
4
3
4
Коэффициенты корреляции: r
1,3
= r
2,3
= r
1,4
= r
2,4
= 0,8.
В этот же момент времени были получены фактические
значения показателей x
1
(Ф)
= 8, x
2
(Ф)
= 22.
Выполнить пассивную коррекцию результатов моделиро-
вания.
1. x
1
(Ф)
= 8, x
2
(Ф)
= 22.
2. Вычисляются уточненные значения параметра х
3
:
;
4
,
17
)
10
8
(
2
3
8
,
0
15
)
x
x
(
r
x
x
1
)
Ɏ
(
1
x
x
13
3
)
3
,
1
(
3
1
3
V
V
.
8
,
13
)
20
–
22
(
4
3
8
,
0
–
15
)
x
–
x
(
r
–
x
x
2
)
Ɏ
(
2
x
x
23
3
)
3
,
2
(
3
2
3
V
V
3. Вычисляются уточненные значения параметра х
4
:
;
2
,
33
)
10
8
(
2
4
8
,
0
30
)
x
x
(
r
x
x
1
)
Ɏ
(
1
x
x
14
4
)
4
,
1
(
4
1
4
V
V
.
4
,
28
)
20
22
(
4
4
8
,
0
30
)
x
x
(
r
x
x
2
)
Ɏ
(
2
x
x
24
4
)
4
,
2
(
4
2
4
V
V
4. Оцениваются значения комбинированного прогноза па-
раметров х
3
и х
4
.
х
3
=(17,4+13,8)/2=15,6; х
4
=(33,2+28,4)/2=30,8.
Рассмотрим один из подходов построения корректируемых
моделей, работающих в реальном масштабе времени.
Если эти модели предназначены для оценки текущих зна-
чений показателей системы, то механизм коррекции может быть
следующим
1
:
1
Здесь рассмотрена модель взаимодействия двух систем (Н) и (П), каж-
дая из которых состоит из определенного количества элементов. Для количе-
ственной оценки состояния систем использован метод динамики моментов.
1. Для вычисления показателей состояния системы (m
i
(п)
и
m
i
(н)
) разработана и используется ее модель, например, на основе
дифференциальных уравнений:
;
,t
R
m
dt
dm
ɧ
n
1
i
)
ɧ
(
j
i
)
ɧ
(
i
j
i
)
ɧ
(
)
ɧ
(
ij
)
ɩ
(
i
¦
F
[
O
,
,
t
R
m
dt
dm
)
ɩ
(
ij
)
ɩ
(
i
)
ɩ
(
ij
n
1
i
(ɩ)
ij
)
ɧ
(
i
ɩ
F
[
O
¦
,
где
)
,
t
(
R
),
,
t
(
R
)
ɩ
(
ij
)
ɧ
(
ij
F
F
— совокупность параметров, харак-
теризующая условия функционирования системы;
)
ɧ
(
ij
)
ɩ
(
ij
ȟ
,
ȟ
, — управления системы;
)
ɩ
(
ij
)
ɧ
(
ij
,
O
O
— интенсивности воздействия i-го элемента на j-й
элемент каждой из подсистем.
n
н
, n
п
— количество элементов подсистем (Н) и (П) соот-
ветственно;
Ввиду наличия методических погрешностей модели теку-
щие численности вычисляются с ошибками.
Для количественной оценки этих ошибок с помощью этой же
модели оцениваются К
i,j
, D
i
, Г
i,j
(К
i,j
— корреляционный момент,
D
i
— дисперсия, Г
i,j
— первый смешанный начальный момент).
2. В начальный момент времени
)
ɩ
(
i
m
= m
iɮ
(ɩ)
;
)
ɧ
(
i
m
= m
iɮ
(ɧ)
;
,
0
;
0
D
;
0
K
0
t
j
i
0
t
i
0
t
j
i
*
где m
iф
(п)
,
m
iф
(н)
— фактические значения текущих значений
взаимодействующих элементов системы.
3. В момент ввода корректирующих данных (пассивная
коррекция):
>
@
0
m
–
m
k
t
t
)
ɧ
(
ip
)
ɧ
(
ɮ
i
;
>
@
0
m
–
m
k
t
t
)
ɩ
(
ip
)
ɩ
(
ɮ
i
;
0
D
k
t
t
)
ɧ
(
i
;
0
D
k
t
t
)
ɩ
(
i
;
,
0
m
m
–
k
t
t
)
ɩ
(
i
)
ɧ
(
i
j
i
*
396
397
где m
ip
(н)
, m
ip
(п)
— расчетные значения численностей в момент
коррекции системы.
После коррекции (для корректируемых параметров) ликви-
дируются ошибки их определения, но не устраняются причины
их возникновения.
Для устранения этих причин в моменты времени, следую-
щие за моментом коррекции, в дифференциальных уравнени-
ях для оценки численностей необходимо учитывать условные
управления.
4. Вычисление и учет условных управлений. При решении
этой задачи принято следующие основные допущения: проме-
жуток времени между двумя последовательными коррекциями
незначителен; моделируемый процесс на интервале коррекции
имеет линейный характер.
Условные управления в этом случае могут быть получены
в результате решения следующей системы уравнений:
0
)
m
–
m
(
–
t
,t
R
m
)
(
1
)
ɩ
(
i
2
)
ɩ
(
ɮ
i
k
n
1
i
)
ɧ
(
j
i
)
ɧ
(
i
)
ɧ
(
j
i
)
ɧ
(
j
i
)
ɧ
(
ij
ɧ
'
F
[
'
[
O
¦
0
)
m
–
m
(
–
t
,t
R
m
)
(
1
)
ɧ
(
i
2
)
ɧ
(
iɮ
k
)
ɩ
(
ij
)
ɩ
(
i
)
ɩ
(
ij
)
ɩ
(
ij
n
1
j
)
ɩ
(
ij
ɩ
'
F
[
'
[
O
¦
,
где
)
ɩ
(
ij
)
ɧ
(
ij
,
[
'
[
'
— условные управления;
t
k
— момент коррекции системы;
t
k
— промежуток времени между двумя последователь-
ными моментами коррекции системы.
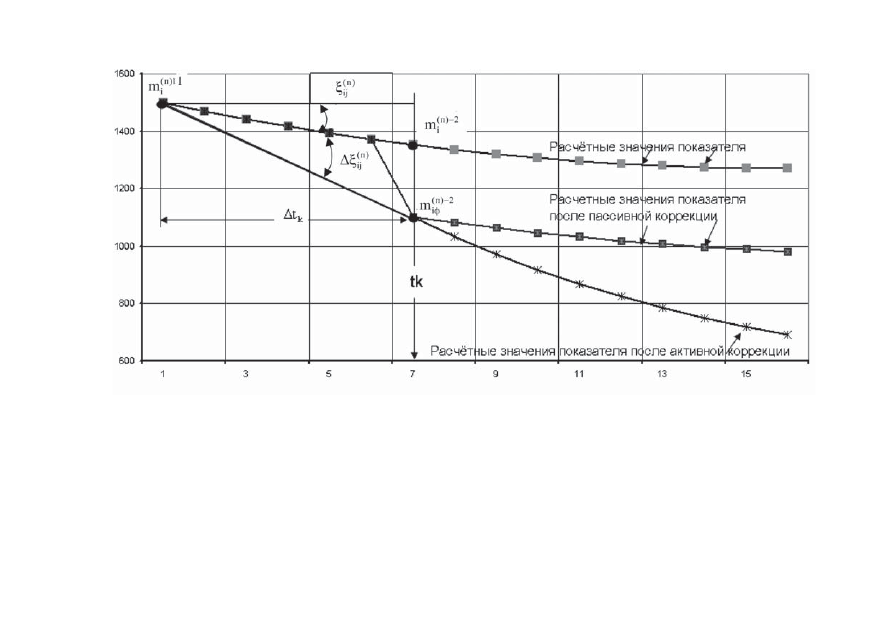
Индексы (1) и (2) определяют значения параметров процесса
на границах промежутка времени между двумя последователь-
ными моментами коррекции системы (рис. 3.9).
Пример. С целью оценивания и прогнозирования показате-
лей функционирования системы (рис. 3.10) используется мате-
матическая модель. Процесс функционирования описывается
с помощью дифференциальных уравнений, позволяющих на
заданный интервал прогнозирования определить значения этих
показателей. В ходе моделирования процесса есть возможность
получить фактические показатели процесса и выполнить кор-
Рис. 3.9.
Определению условных управлений системы
396
397
где m
ip
(н)
, m
ip
(п)
— расчетные значения численностей в момент
коррекции системы.
После коррекции (для корректируемых параметров) ликви-
дируются ошибки их определения, но не устраняются причины
их возникновения.
Для устранения этих причин в моменты времени, следую-
щие за моментом коррекции, в дифференциальных уравнени-
ях для оценки численностей необходимо учитывать условные
управления.
4. Вычисление и учет условных управлений. При решении
этой задачи принято следующие основные допущения: проме-
жуток времени между двумя последовательными коррекциями
незначителен; моделируемый процесс на интервале коррекции
имеет линейный характер.
Условные управления в этом случае могут быть получены
в результате решения следующей системы уравнений:
0
)
m
–
m(
–
t
,t
R
m)
(
1)
ɩ(
i
2)
ɩ(
ɮi
k
n
1
i
)ɧ
(
ji
)ɧ
(
i
)ɧ
(
ji
)ɧ
(
ji
)ɧ
(
ij
ɧ
'
F
['
[
O
¦
0
)
m
–
m(
–
t
,t
R
m)
(
1)
ɧ(
i
2)
ɧ(
iɮ
k
)ɩ
(
ij
)ɩ
(
i
)ɩ
(
ij
)ɩ
(
ij
n
1
j
)ɩ
(
ij
ɩ
'
F
['
[
O
¦
,
где
)ɩ
(
ij
)ɧ
(
ij
,
[
'
[
'
— условные управления;
t
k
— момент коррекции системы;
t
k
— промежуток времени между двумя последователь-
ными моментами коррекции системы.
Индексы (1) и (2) определяют значения параметров процесса
на границах промежутка времени между двумя последователь-
ными моментами коррекции системы (рис. 3.9).
Пример.
С целью оценивания и прогнозирования показате-
лей функционирования системы (рис. 3.10) используется мате-
матическая модель. Процесс функционирования описывается
с помощью дифференциальных уравнений, позволяющих на
заданный интервал прогнозирования определить значения этих
показателей. В ходе моделирования процесса есть возможность
получить фактические показатели процесса и выполнить кор-
Рис. 3.9. Определению условных управлений системы
398
399
рекцию модели. Для условий моделирования, приведенных в
табл. 3.5, выполнить пассивную и активную коррекцию моде-
лируемого процесса с целью повышения точности оценивания
показателей на заданный интервал прогнозирования.
ɉɨɞɫɢɫɬɟɦɚ (ɇ)
ɉɨɞɫɢɫɬɟɦɚ(ɉ)
ɩɧ
O
ɧɩ
O
m
(ɩ)
m
(ɧ)
Рис. 3.10. Графическое изображение корректируемой системы
В простейшем случае так может быть изображена модель
взаимодействующих и конкурирующих предприятий с экономи-
ческим потенциалом каждого m
(н)
и m
(п)
. Каждое из предприятий
воздействует на другое физическими, информационными и
другими свойствами, ослабляя экономический потенциал кон-
курента с интенсивностями
пн
,
нп
(условно на одну единицу в
единицу времени — 1/сут.).
Таблица 3.5
Подсисте-
мы
Началь-
ное со-
стояние
(m)
Расчетное
состояние
в момент
коррекции
(m
р
)
Факти-
ческое
состоя-
ние в
момент
коррек-
ции (m
ф
)
Интен-
сив-
ность
воздей-
ствия
(
)
Время
коррек-
ции си-
стемы,
сут.
Ин-
тервал
прогно-
зирова-
ния, сут.
Подсисте-
ма (Н)
1000
570,28
650
0,03
6
14
Подсисте-
ма (П)
1500
1352,9
1100
0,05
Решение
1. Решается система дифференциальных уравнений (рис. 3.11)
и строятся графические зависимости, характеризующие со-
стояние системы (рис. 3.12).
текущие значения показателей, характеризующих со-
стояние системы:
)
ɩ
(
ɧɩ
)
ɧ
(
m
dt
dm
O
;
)
ɧ
(
ɩɧ
)
ɩ
(
m
dt
dm
O
;
дисперсии определения ошибок показателей, характери-
зующих состояние системы:
)
ɩ
(
ɧɩ
ɧ
m
dt
dD
O
;
)
ɧ
(
ɩɧ
ɩ
m
dt
dD
O
.
2. Вычисляется управление (интенсивности воздействий),
переводящее систему в фактическое состояние в момент кор-
рекции.
6
1100
1000
650
–
t
m
m
m
–
Ȝ
ɤɨɪ
(ɩ)
ɮ
)
ɧ
(
o
(ɧ)
ɮ
(ɧ)
ɮ
= 0,053;
6
650
1500
–
1100
–
t
m
m
m
–
Ȝ
ɤɨɪ
(ɧ)
ɮ
(ɩ)
ɪ
(ɩ)
ɮ
(ɩ)
ɮ
= 0,102
6
1352,9
1000
570,28
–
t
m
m
m
–
Ȝ
ɤɨɪ
(ɩ)
p
(ɧ)
0
(ɧ)
ɪ
(ɧ)
ɪ
= 0,0529;
ɤɨɪ
(ɧ)
p
(ɩ)
0
(ɩ)
ɪ
(ɩ)
(ɪ)
t
m
m
m
–
Ȝ
= –
6
28
,
570
1500
9
,
1352
= 0,0429.
Дисперсии определения ошибок показателей функциони-
рования подсистем (П) и (Н) в момент коррекции системы равны
нулю, т. е. D
п
*
=D
н
*
=0.
3. Строятся зависимости, характеризующие состояние
системы после выполнения коррекции модели. (вводятся пока-
затели состояния и условные управления).
4. Оцениваются значения показателей, характеризующие
состояние системы на 14-е сутки ее функционирования:
при отсутствии коррекции системы:
m
(н)
=47,5, m
(п)
=1271,6;
D
н
=952, D
п
=228;
при пассивной коррекции системы:
)
ɧ
(
ɮ
m
=232,78,
)
ɩ
(
ɮ
m
=988,73;
при активной коррекции системы:
)
ɧ
(
ɮ
m
=265,58;
)
ɩ
(
ɮ
m
=718,1;
D
н
=326, D
п
=315.
398
399
рекцию модели. Для условий моделирования, приведенных в
табл. 3.5, выполнить пассивную и активную коррекцию моде-
лируемого процесса с целью повышения точности оценивания
показателей на заданный интервал прогнозирования.
ɉɨɞɫɢɫɬɟɦɚ (ɇ)
ɉɨɞɫɢɫɬɟɦɚ(ɉ)
ɩɧ
O
ɧɩ
O
m
(ɩ)
m
(ɧ)
Рис. 3.10. Графическое изображение корректируемой системы
В простейшем случае так может быть изображена модель
взаимодействующих и конкурирующих предприятий с экономи-
ческим потенциалом каждого m
(н)
и m
(п)
. Каждое из предприятий
воздействует на другое физическими, информационными и
другими свойствами, ослабляя экономический потенциал кон-
курента с интенсивностями
пн
,
нп
(условно на одну единицу в
единицу времени — 1/сут.).
Таблица 3.5
Подсисте-
мы
Началь-
ное со-
стояние
(m)
Расчетное
состояние
в момент
коррекции
(m
р
)
Факти-
ческое
состоя-
ние в
момент
коррек-
ции (m
ф
)
Интен-
сив-
ность
воздей-
ствия
(
)
Время
коррек-
ции си-
стемы,
сут.
Ин-
тервал
прогно-
зирова-
ния, сут.
Подсисте-
ма (Н)
1000
570,28
650
0,03
6
14
Подсисте-
ма (П)
1500
1352,9
1100
0,05
Решение
1. Решается система дифференциальных уравнений (рис. 3.11)
и строятся графические зависимости, характеризующие со-
стояние системы (рис. 3.12).
текущие значения показателей, характеризующих со-
стояние системы:
)
ɩ
(
ɧɩ
)
ɧ
(
m
dt
dm
O
;
)
ɧ
(
ɩɧ
)
ɩ
(
m
dt
dm
O
;
дисперсии определения ошибок показателей, характери-
зующих состояние системы:
)
ɩ
(
ɧɩ
ɧ
m
dt
dD
O
;
)
ɧ
(
ɩɧ
ɩ
m
dt
dD
O
.
2. Вычисляется управление (интенсивности воздействий),
переводящее систему в фактическое состояние в момент кор-
рекции.
6
1100
1000
650
–
t
m
m
m
–
Ȝ
ɤɨɪ
(ɩ)
ɮ
)
ɧ
(
o
(ɧ)
ɮ
(ɧ)
ɮ
= 0,053;
6
650
1500
–
1100
–
t
m
m
m
–
Ȝ
ɤɨɪ
(ɧ)
ɮ
(ɩ)
ɪ
(ɩ)
ɮ
(ɩ)
ɮ
= 0,102
6
1352,9
1000
570,28
–
t
m
m
m
–
Ȝ
ɤɨɪ
(ɩ)
p
(ɧ)
0
(ɧ)
ɪ
(ɧ)
ɪ
= 0,0529;
ɤɨɪ
(ɧ)
p
(ɩ)
0
(ɩ)
ɪ
(ɩ)
(ɪ)
t
m
m
m
–
Ȝ
= –
6
28
,
570
1500
9
,
1352
= 0,0429.
Дисперсии определения ошибок показателей функциони-
рования подсистем (П) и (Н) в момент коррекции системы равны
нулю, т. е. D
п
*
=D
н
*
=0.
3. Строятся зависимости, характеризующие состояние
системы после выполнения коррекции модели. (вводятся пока-
затели состояния и условные управления).
4. Оцениваются значения показателей, характеризующие
состояние системы на 14-е сутки ее функционирования:
при отсутствии коррекции системы:
m
(н)
=47,5, m
(п)
=1271,6;
D
н
=952, D
п
=228;
при пассивной коррекции системы:
)
ɧ
(
ɮ
m
=232,78,
)
ɩ
(
ɮ
m
=988,73;
при активной коррекции системы:
)
ɧ
(
ɮ
m
=265,58;
)
ɩ
(
ɮ
m
=718,1;
D
н
=326, D
п
=315.