Файл: Образовательное учреждение высшего образования уфимский университет науки и технологий.docx
Добавлен: 12.01.2024
Просмотров: 134
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Они представляют собой совокупности пар рациональных сплайнов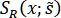 
и 
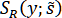. В качестве параметра будем брать по-прежнему суммарную длину хорд. Каждый из сплайнов 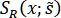и 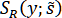представляется на участке между точками 
в виде
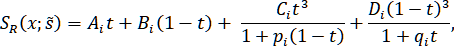
где – заданные числа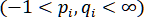
. Величины целесообразно выбирать одинаковыми для обоих сплайнов.
Параметрический рациональный сплайн при
,
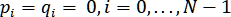превращается в параметрический кубический сплайн.
В пределе при
,
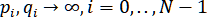имеем параметрический сплайн первой степени.
Выбором величин обычно удаётся при относительно малом числе узлов интерполяции обеспечить и высокую точность приближения, и хорошие качественные характеристики. Например, выбирая их достаточно большими, можно полностью устранить осцилляции.
Ряд важных результатов теории и практики сплайнов связан со свойствами матриц с диагональным преобладанием.
Так, квадратная матрица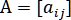
порядка называется матрицей с диагональным преобладанием, если выполняются условия
Многие задачи теории сплайнов приводят к решению систем линейных уравнений с ленточными матрицами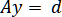
.
Величина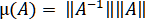
называется мерой (числом) обусловленности системы или матрицы. Системы уравнений и матрицы с небольшими значениями мер обусловленности принято всегда называть хорошо обусловленными.
Если – матрица с диагональным преобладанием, то воспользуемся оценкой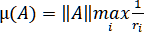
, где определяется из (2.4.1).
Если величина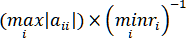
невелика, то – хорошо
обусловленная матрица.
Применим метод прогонки для решения систем уравнений с трёхдиагональными матрицами.
Пусть имеется система
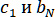отличны от нуля.
Будем искать в виде
. (2.4.2)
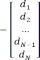
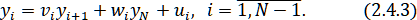
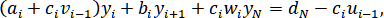Подставив выражение для из (2.4.3) в -e уравнение системы, получаем
где
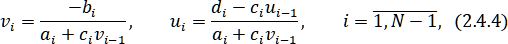
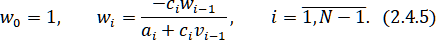
Теперь выразим все через в виде
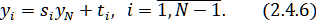
Подставляя выражение для в (2.4.3), получаем
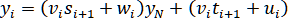
Сравнивая это соотношение с (2.4.6), находим рекуррентные формулы для величин
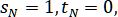
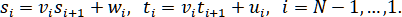(2.4.7)
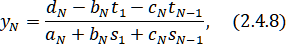
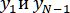Подставляя из (6.6) в последнее уравнение системы (2.4.2), находим
после чего решение вычисляется по формулам (2.4.6). Всего необходимо выполнить арифметических операций: сложений, умножений и делений.
При решении серии систем с одинаковой матрицей предварительно следует вычислить и запомнить независящие от правой части величины: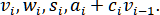
Тогда для решения каждой из систем потребуется арифметических операций.
Алгоритм называется корректным, если все действия, необходимые для его реализации, выполнимы. Исследование корректности алгоритма прогонки сводится к выяснению условий, при которых знаменатели в формулах (2.4.4), (2.4.5), (2.4.8) не равны нулю.
Будем называть алгоритм устойчивым, если выполняются неравенства
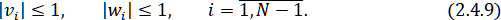
В этом случае при счете по формулам (2.4.4), (2.4.5) – (2.4.7) не происходит прогрессивного накопления погрешностей округления за счет операций умножения.
Убедимся в корректности и устойчивости системы.
Установим неравенства
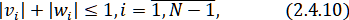
из которых вытекают неравенства (2.4.9). Имеем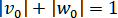
. Тогда предположим, что (2.4.10) выполняется при .
Тогда
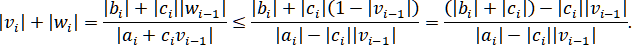
Так как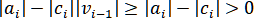
и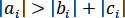 
, то отсюда следует, что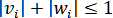 
. Неравенства (2.4.10) доказаны. Также установлено, что знаменатель в формулах (2.4.4), (2.4.5) отличен от нуля. Кроме того, из
(2.4.7) вытекает, что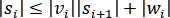
. Также знаменатель в формуле (2.4.8) не обращается в нуль, так как
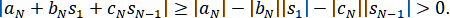
По разработанной программе были получены результаты, представленные на рисунках.
Рисунок 3.1. Рисунок 3.2.
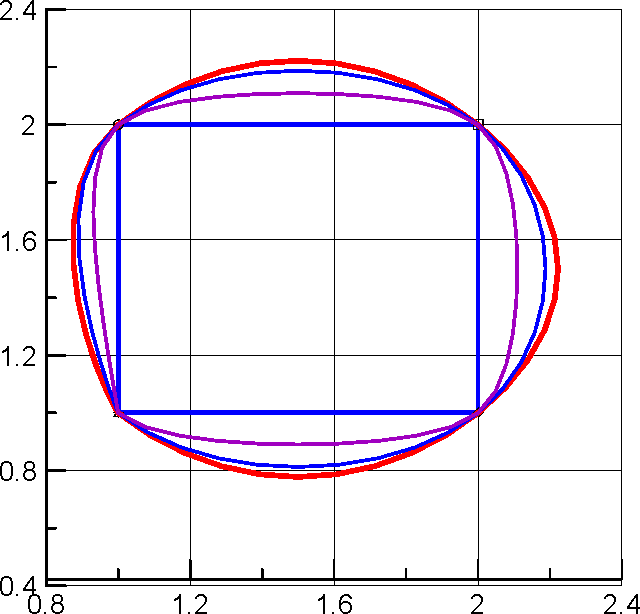
N = 7, 1 – линейный сплайн, 2 – кубический, 3 – рациональный
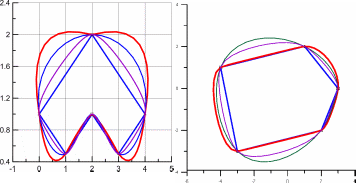
Рисунок 3.3.
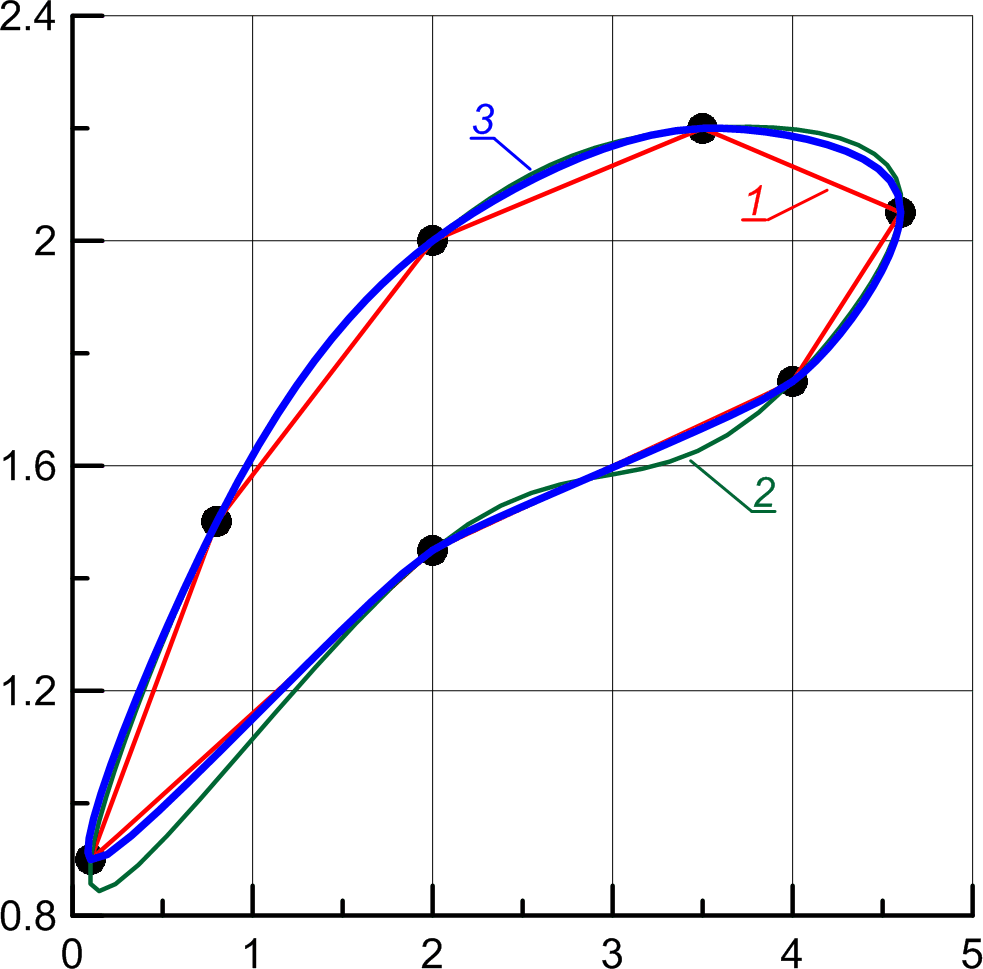
. 1– линейный сплайн; 2– кубический сплайн; 3– рациональный сплайн (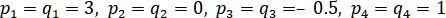
).
Рисунок 3.4.
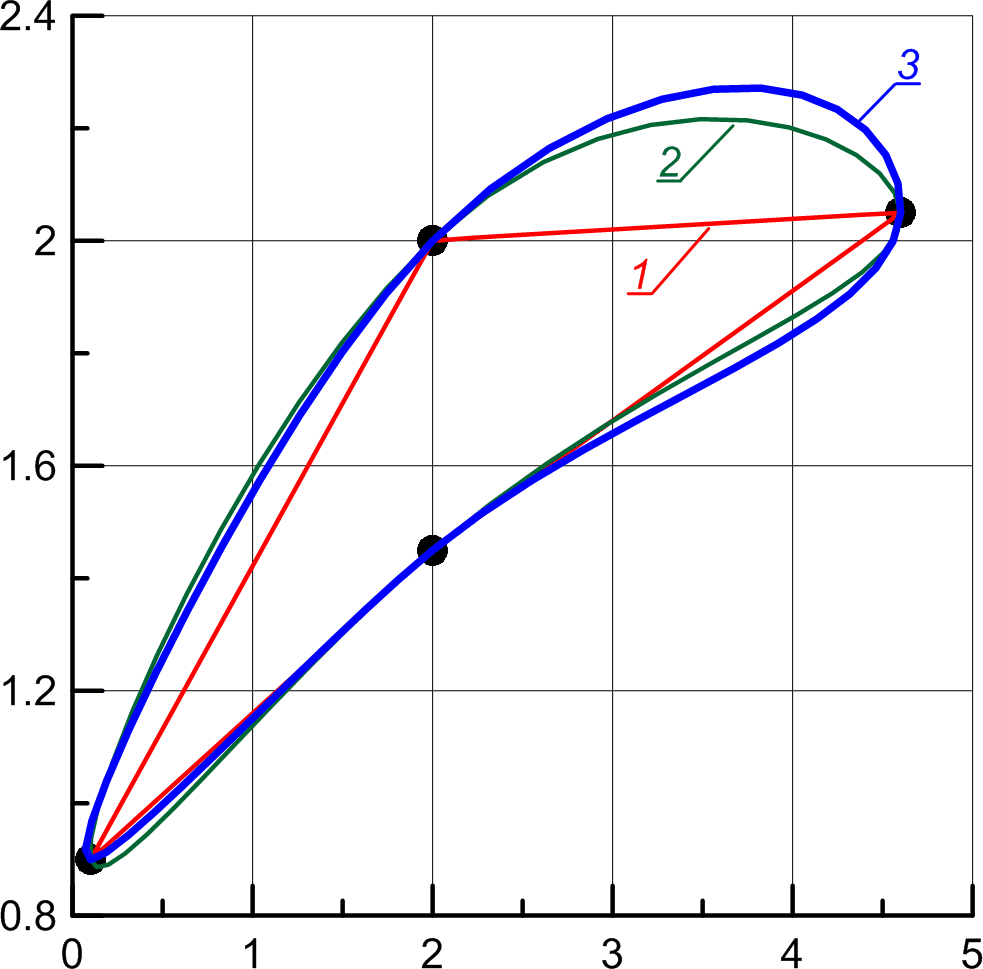
Рисунок 3.
и . В качестве параметра будем брать по-прежнему суммарную длину хорд. Каждый из сплайнов и представляется на участке между точками в виде где – заданные числа
. Величины целесообразно выбирать одинаковыми для обоих сплайнов.Параметрический рациональный сплайн при
,превращается в параметрический кубический сплайн.
В пределе при
,имеем параметрический сплайн первой степени.
Выбором величин обычно удаётся при относительно малом числе узлов интерполяции обеспечить и высокую точность приближения, и хорошие качественные характеристики. Например, выбирая их достаточно большими, можно полностью устранить осцилляции.
-
Метод прогонки
Ряд важных результатов теории и практики сплайнов связан со свойствами матриц с диагональным преобладанием.
Так, квадратная матрица
порядка называется матрицей с диагональным преобладанием, если выполняются условия
Многие задачи теории сплайнов приводят к решению систем линейных уравнений с ленточными матрицами
.Величина
называется мерой (числом) обусловленности системы или матрицы. Системы уравнений и матрицы с небольшими значениями мер обусловленности принято всегда называть хорошо обусловленными.Если – матрица с диагональным преобладанием, то воспользуемся оценкой
, где определяется из (2.4.1).Если величина
невелика, то – хорошообусловленная матрица.
Применим метод прогонки для решения систем уравнений с трёхдиагональными матрицами.
Пусть имеется система
отличны от нуля.Будем искать в виде
. (2.4.2)
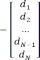
Подставив выражение для из (2.4.3) в -e уравнение системы, получаемгде
Теперь выразим все через в виде
Подставляя выражение для в (2.4.3), получаем
Сравнивая это соотношение с (2.4.6), находим рекуррентные формулы для величин
(2.4.7) Подставляя из (6.6) в последнее уравнение системы (2.4.2), находимпосле чего решение вычисляется по формулам (2.4.6). Всего необходимо выполнить арифметических операций: сложений, умножений и делений.
При решении серии систем с одинаковой матрицей предварительно следует вычислить и запомнить независящие от правой части величины:
Тогда для решения каждой из систем потребуется арифметических операций.Алгоритм называется корректным, если все действия, необходимые для его реализации, выполнимы. Исследование корректности алгоритма прогонки сводится к выяснению условий, при которых знаменатели в формулах (2.4.4), (2.4.5), (2.4.8) не равны нулю.
Будем называть алгоритм устойчивым, если выполняются неравенства
В этом случае при счете по формулам (2.4.4), (2.4.5) – (2.4.7) не происходит прогрессивного накопления погрешностей округления за счет операций умножения.
Убедимся в корректности и устойчивости системы.
Установим неравенства
из которых вытекают неравенства (2.4.9). Имеем
. Тогда предположим, что (2.4.10) выполняется при .Тогда
Так как
и , то отсюда следует, что
. Неравенства (2.4.10) доказаны. Также установлено, что знаменатель в формулах (2.4.4), (2.4.5) отличен от нуля. Кроме того, из
(2.4.7) вытекает, что
. Также знаменатель в формуле (2.4.8) не обращается в нуль, так как - 1 2 3 4
РЕЗУЛЬТАТЫ РАСЧЁТОВ
По разработанной программе были получены результаты, представленные на рисунках.
Рисунок 3.1. Рисунок 3.2.
N = 7, 1 – линейный сплайн, 2 – кубический, 3 – рациональный
Рисунок 3.3.
. 1– линейный сплайн; 2– кубический сплайн; 3– рациональный сплайн (
).Рисунок 3.4.
Рисунок 3.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
-
Бабенко К.И. Основы численного анализа. М.: Наука, 1986. 744 с. -
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 2006. 636 с. -
Бахвалов Н.С., Кобельков Г.М., Кузнецов В.И. Современные проблемы вычислительной математики и математического моделирования: в 2 т. М: Наука, 2005. 343 с., 405 с. -
Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. М.: Мир, 1984. 490 с. -
Болотнов А.М. Методы граничных элементов в расчетах электрических полей электрохимических систем. Уфа: РИО БашГУ, 2002. 144 с. -
Болотнов А.М. Разработка программных приложений в среде BlackBox: Учебное пособие. СПб.: Издательство "Лань", 2018. 144 с. -
Бреббия К., Телес Ж., Вроубель Л. Методы граничных элементов. М.: Мир. 1987. 524 с. -
Верлань А.Ф., Сизиков В.С. Интегральные уравнения: методы, алгоритмы, программы. Справочное пособие. Киев: Наукова Думка, 1986. 543 с. -
Вержбицкий В. М. Основы численных методов: Учебник для вузов. М.: Высш. шк., 2002. 840 с. -
Воеводин В.В. Ошибки округления и устойчивость в прямых методах линейной алгебры. М.: Изд-во МГУ, 1969. 153 с. -
Волков Е.А. Численные методы. М: Наука, 1987. 248 с. -
Голованов, Н.Н. Геометрическое моделирование. М.: Изд-во физико- математической литературы, 2002. 472 с. -
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967. 368 с. -
Завьялов Ю.С., Квасов Б.И., Мирошниченко В.П. Методы сплайн- функций. М.: Наука, 1980. 352 с. -
Ильин В.П. Численные методы решения задач электрофизики. М.: Наука, 1985. 334 с. -
Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир, 2001. 575 с. -
Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М.: ВШ. 2004. 480 с. -
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1989. 624 с.