Файл: Образовательное учреждение высшего образования уфимский университет науки и технологий.docx
Добавлен: 12.01.2024
Просмотров: 132
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СПЛАЙНЫ ПЕРВОЙ СТЕПЕНИ, КУБИЧЕСКИЕ И РАЦИОНАЛЬНЫЕ СПЛАЙНЫ
-
Определение сплайна
Сплайн представляет собой функцию, область определения которой разбита на конечное количество отрезков, на любом из которых сплайн схож с неким алгебраическим полиномом. Наибольшая степень из выбранных полиномов называется степенью сплайна. Гладкость сплайна – максимальный порядок непрерывной производной. Разница между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Так, постоянная ломаная – это сплайн степени 1 и дефекта 1.
Пусть на участке отрезка [а, b] дано разбиение :
В данном случае для целочисленного через
Как следует из работы Бахвалова Н.С. Численные методы, «Широкое
распространение сплайнов во многом вызвано тем, что они являются в определённом смысле наиболее гладкими функциями среди функций, принимающих заданные значения. Сплайны степени выше первой в случае гладкой хорошо
приближают не только саму функцию, но и её производные».
а) на каждом отрезке
б)
Определение кусочно-непрерывной функции остаётся целесообразным на всей вещественной оси, при условии, что
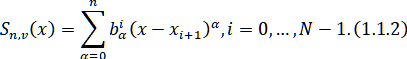
В этой связи на полуоси
используется формула (1.1.1).
Из этого следует, что сплайн
, непрерывна справа, т. е.
Множество сплайнов, соответствующих определению, обозначим через
«Использование обычных операций сложения элементов из
Несложным примером сплайна считается единичная функция Хевисайда:
Также с ней связана и усечённая степенная функция:
Функции и являются «сплайнами
соответственно нулевой степени и степени n дефекта 1 с единственным узлом в нулевой точке» (рисунок 1.1).
Мы будем рассматривать также усечённые степенные функции
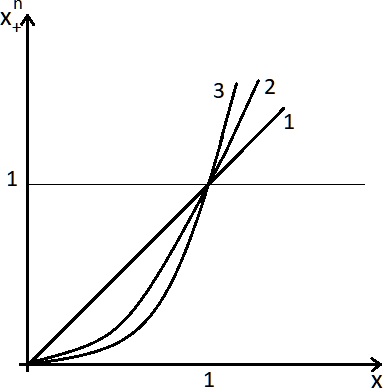
Сплайн нулевой степени и степени n дефекта 1 Рисунок 1.1
Пусть – заданная на отрезке
Если выполняется только часть из двух данных условий, то такой сплайн называется локальным интерполяционным сплайном.
-
Сплайн первой степени
Сплайны первой степени
Пусть в узлах сетки заданы значения
, которая определяется на
отрезке
определяется с помощью условий:
Можно представить его геометрически: получим линии, похожие на ломаные, проходящие через точки ( ) , где (рисунок 1.2).
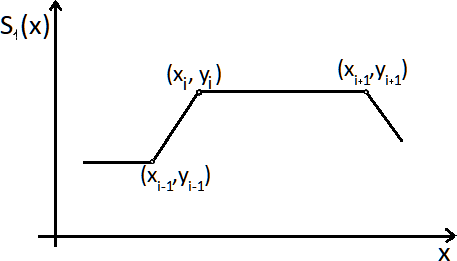
Интерполяционный линейный сплайн.
Рисунок 1.2
или
Если величина задана с погрешностью, не превосходящей ε, то значения
-
Определение кубических сплайнов
Возьмём отрезок
Интерполяционным кубическим сплайном