Файл: Образовательное учреждение высшего образования уфимский университет науки и технологий.docx
Добавлен: 12.01.2024
Просмотров: 137
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
I:
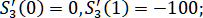
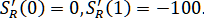
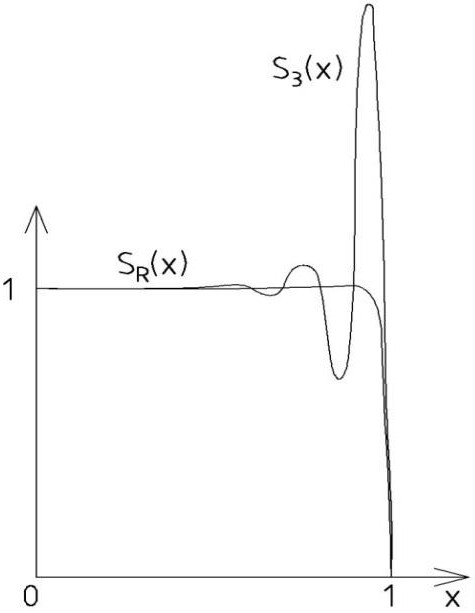
Графики интерполяционных сплайнов.
Рисунок 1.3 Сплайн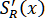 составлялся с параметрами:
составлялся с параметрами:
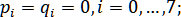
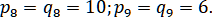
Удобным способом приближения кривых является параметрическое задание их координат в виде двух функций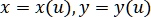 некоторого параметра .
некоторого параметра .
При интерполяции кривой, заданной параметрически, естественно ввести
разбиение на промежутке изменения параметра :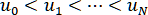 , следующим шагом требуется вычислить соответствующие значения координат точек на кривой,
, следующим шагом требуется вычислить соответствующие значения координат точек на кривой, 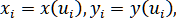 и построить для функций
и построить для функций 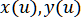 интерполяционные сплайны
интерполяционные сплайны 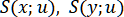 . Совокупность этих двух сплайнов называют интерполяционным параметрическим сплайном. В зависимости от вида функций
. Совокупность этих двух сплайнов называют интерполяционным параметрическим сплайном. В зависимости от вида функций 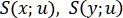 будем говорить о параметрических сплайнах первой степени, эрмитовых параметрических сплайнах.
будем говорить о параметрических сплайнах первой степени, эрмитовых параметрических сплайнах.
Для расчёта погрешности приближения кривой параметрическим сплайном воспользуемся величиной
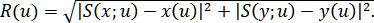 (2.1)
(2.1)
При выполнении определённых требований к гладкости функций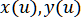 можно оценить выражения
можно оценить выражения 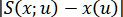
,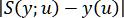 по какой-либо норме, например, пространства С. Тогда
по какой-либо норме, например, пространства С. Тогда
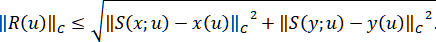 (2.2)
(2.2)
Главной особенностью задач о приближении кривых является то, что заданы бывают только упорядоченные массивы точек на них, а информация о способе параметризации, которая необходима для построения сплайнов, отсутствует. Построение интерполяционных параметрических сплайнов для пространственных кривых можно осуществить и аналогичным образом. Разница лишь в том, что приходится оперировать с совокупностью трёх сплайнов одной переменной [14].
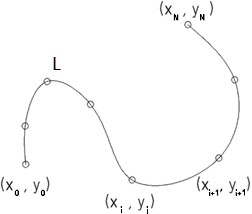 Предположим, что на некоторой кривой L задана последовательность точек
Предположим, что на некоторой кривой L задана последовательность точек 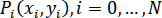 (рисунок 2.1). Введём на ней естественную параметризацию
(рисунок 2.1). Введём на ней естественную параметризацию 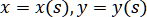 , взяв в качестве параметра длину дуги s кривой, которая отсчитывается от точки . Узлу будет соответствовать значение параметра .
, взяв в качестве параметра длину дуги s кривой, которая отсчитывается от точки . Узлу будет соответствовать значение параметра .
Рисунок 2.1
Рассмотрим интерполяционный параметрический сплайн первой степени.
На промежутке между точками и он задается соотношениями
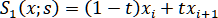 , (2.1.1)
, (2.1.1)
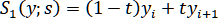 , где
, где 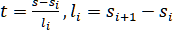
.
Геометрически параметрический сплайн первой степени представляет собой ломаную, которая состоит из отрезков прямых, соединяющих точки .
Из формулы (2.1.1) следует, что
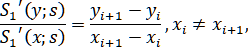
которое используют для приближенного нахождения наклона касательной к кривой L между точками и . Если , то отсюда следует, что данное звено сплайна будет расположено параллельно оси .
Интерполяционным параметрическим кубическим сплайном именуется совокупность двух кубических сплайнов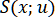 ,
, 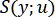 класса , интерполирующих соответственно координаты точек
класса , интерполирующих соответственно координаты точек 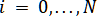 , кривой на сетке :
, кривой на сетке :  [14]. Для того, чтобы однозначно определить каждый из этих сплайнов, зададим краевые условия. Если кривая незамкнутая, то применим условие типа IV, а если замкнутая – соответственно используем краевое условие типа III.
[14]. Для того, чтобы однозначно определить каждый из этих сплайнов, зададим краевые условия. Если кривая незамкнутая, то применим условие типа IV, а если замкнутая – соответственно используем краевое условие типа III.
В качестве параметра будем использовать суммарную длину хорд .
Запишем сплайн в виде
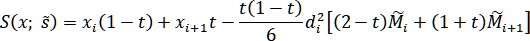
где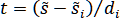 , = .
, = .
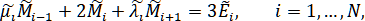 Выпишем систему
Выпишем систему
для нахождения величины для периодических сплайнов
где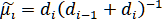 ,
, 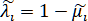 ,
,
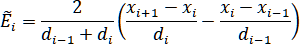
Аналогичные формулы имеют место и для сплайна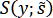 .
.
Погрешность интерполяции параметрическим кубическим сплайном определим формулой
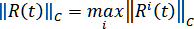 ,
,
где положим
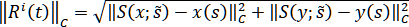 .
.
Сравнение сплайнов и интерполируемых функций делается при
одинаковых значениях параметра . Получим оценки погрешности интерполяции.
Наряду со сплайном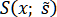 используем и сплайн
используем и сплайн 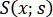 , построенный с использованием параметризации по длине дуги:
, построенный с использованием параметризации по длине дуги:
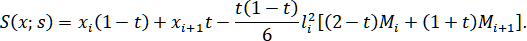
здесь вычисляются из системы
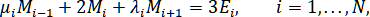
где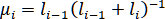 ,
, 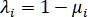 ,
,
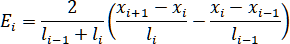
Среди всех сплайнов, используемых при аппроксимации кривых, наиболее универсальными свойствами обладают параметрические рациональные сплайны.

Графики интерполяционных сплайнов.
Рисунок 1.3 Сплайн
- 1 2 3 4
ПАРАМЕТРИЧЕСКИЕ СПЛАЙНЫ
Удобным способом приближения кривых является параметрическое задание их координат в виде двух функций
При интерполяции кривой, заданной параметрически, естественно ввести
разбиение на промежутке изменения параметра :
Для расчёта погрешности приближения кривой параметрическим сплайном воспользуемся величиной
При выполнении определённых требований к гладкости функций
,
Главной особенностью задач о приближении кривых является то, что заданы бывают только упорядоченные массивы точек на них, а информация о способе параметризации, которая необходима для построения сплайнов, отсутствует. Построение интерполяционных параметрических сплайнов для пространственных кривых можно осуществить и аналогичным образом. Разница лишь в том, что приходится оперировать с совокупностью трёх сплайнов одной переменной [14].
-
Интерполяция кривых локальными сплайнами
 Предположим, что на некоторой кривой L задана последовательность точек
Предположим, что на некоторой кривой L задана последовательность точек Рисунок 2.1
Рассмотрим интерполяционный параметрический сплайн первой степени.
На промежутке между точками и он задается соотношениями
.
Геометрически параметрический сплайн первой степени представляет собой ломаную, которая состоит из отрезков прямых, соединяющих точки .
Из формулы (2.1.1) следует, что
которое используют для приближенного нахождения наклона касательной к кривой L между точками и . Если , то отсюда следует, что данное звено сплайна будет расположено параллельно оси .
-
Интерполяционный параметрический кубический сплайн
Интерполяционным параметрическим кубическим сплайном именуется совокупность двух кубических сплайнов
В качестве параметра будем использовать суммарную длину хорд .
Запишем сплайн в виде
где
для нахождения величины для периодических сплайнов
где
Аналогичные формулы имеют место и для сплайна
Погрешность интерполяции параметрическим кубическим сплайном определим формулой
где положим
Сравнение сплайнов и интерполируемых функций делается при
одинаковых значениях параметра . Получим оценки погрешности интерполяции.
Наряду со сплайном
здесь вычисляются из системы
где
-
Интерполяционный параметрический рациональный сплайн
Среди всех сплайнов, используемых при аппроксимации кривых, наиболее универсальными свойствами обладают параметрические рациональные сплайны.