Файл: Образовательное учреждение высшего образования уфимский университет науки и технологий.docx
Добавлен: 12.01.2024
Просмотров: 139
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
сплайн, необходимо использовать краевые условия. Рассмотрим четыре типа краевых условий:
I.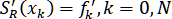 .
.
II.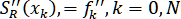 .
.
III. Условия периодичности: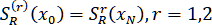 .
.
IV.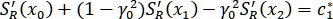 ,
,
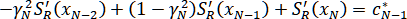 ,
,
где ,
,  ,
,
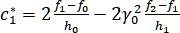 ,
, 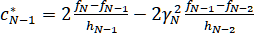 .
.
Можно заметить, что первые три типа условий одинаковы по форме и содержанию с подобными условиями для кубических сплайнов. Содержание условий типа IV раскроем в алгоритме.
1.6 Алгоритм построения интерполяционного рационального сплайна
Из условий интерполяции получим
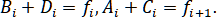
Подставив эти выражения для , в (1.5.1), получим
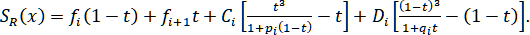 (1.5.3)
(1.5.3)
Сплайн (1.5.3) непрерывен в узлах сетки и удовлетворяет условиям (1.5.2). Определим коэффициенты так, чтобы были непрерывны его первая и вторая производные.
Если
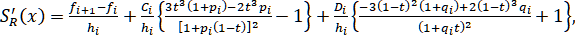 (1.5.4)
(1.5.4)
то
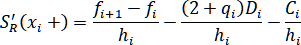
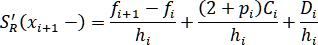
Обозначив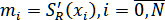 , получим
, получим
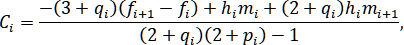
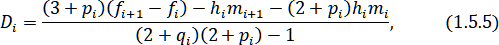
Формулы (1.5.5) являются следствием непрерывности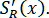 Из (1.5.4)
Из (1.5.4)
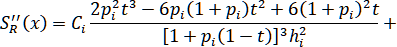
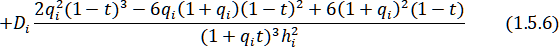
Значит,
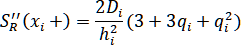
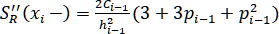 ,
,
и условие непрерывности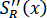 в точке имеет вид
в точке имеет вид
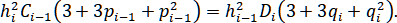
Подставляя сюда и из (1.5.5), получим
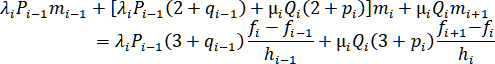
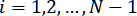 ,
,
где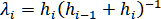 ,
, 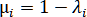 ,
,
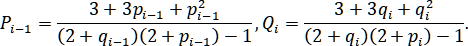
Выпишем системы уравнений относительно неизвестных для каждого вида краевых условий.
Типы I и II.
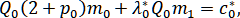
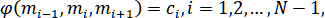
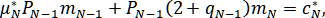
где для типа I:
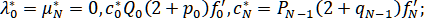
для типа II:
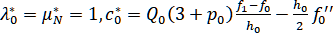 ,
,
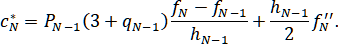
Тип III:
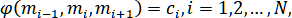
причём
(1.5.7)
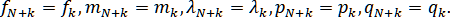
Тип IV:
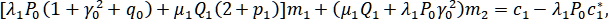
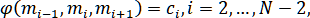
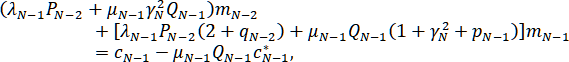
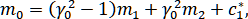
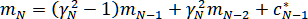 .
.
Матрицы всех полученных систем с диагональным преобладанием. Это открывает перспективы для их решения с помощью метода прогонки и гарантирует существование и единственность интерполяционного рационального сплайна при любом типе краевых условий. После вычисления значений
при любом типе краевых условий. После вычисления значений 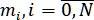 , по формулам (1.5.5) определяются коэффициенты Вычисление сплайна и его 1-ой и 2-ой производных находится с помощью формул (1.5.3), (1.5.4), (1.5.6). В довершении дадим формулу для вычисления 3-ей производной
, по формулам (1.5.5) определяются коэффициенты Вычисление сплайна и его 1-ой и 2-ой производных находится с помощью формул (1.5.3), (1.5.4), (1.5.6). В довершении дадим формулу для вычисления 3-ей производной
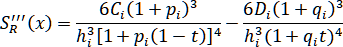
При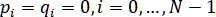 , рациональный сплайн станет кубическим.
, рациональный сплайн станет кубическим.
1.7. Периодический случай
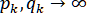 Можно говорить, что сплайн первой степени также является частным случаем рационального сплайна. Проанализируем поведение
Можно говорить, что сплайн первой степени также является частным случаем рационального сплайна. Проанализируем поведение 
на некотором промежутке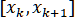 в случае, если ,
в случае, если , 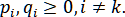 Сетку считаем фиксированной.
Сетку считаем фиксированной.
Теорема. Если A – матрица с диагональным преобладанием, то справедлива оценка
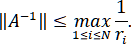
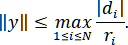 Следствие. Если матрица системы с диагональным преобладанием, то
Следствие. Если матрица системы с диагональным преобладанием, то
Используя данное следствие, из системы (1.5.7) получаем
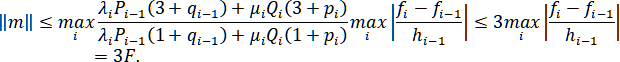
Из (1.5.5) получим
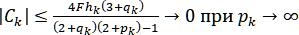 ,
,
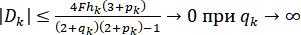 .
.
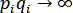 Используя формулу (1.5.3), найдём при
Используя формулу (1.5.3), найдём при 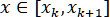
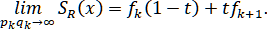
В частности, если для всех одновременно , то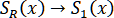 , т.е. сплайн первой степени является предельным случаем рационального сплайна.
, т.е. сплайн первой степени является предельным случаем рационального сплайна.
Рациональные сплайны обладают свойствами наиболее часто встреча- ющихся на практике – сплайнов первой степени и кубических. Кубические сплайны показывают, чаще всего, высокую точность приближения гладких функций. Но при этом не всегда получается удовлетворить требованиям качественного характера. К примеру, если интерполируемая функция выпукла, то в некоторых случаях необходимо, чтобы и сплайн был выпуклым. Кубический
сплайн удовлетворяет этому требованию далеко не
всегда. Сплайн же первой степени в данной ситуации тоже будет выпуклым, но не всегда возможно получить необходимую точность приближения. Кроме всего прочего, сплайн первой степени не является гладкой функцией. Значимые проблемы могут возникнуть при приближении функции с большими градиентами. Использование в данном случае как кубических сплайнов, так и сплайнов первой степени, обычно связано с большим количеством узлов интерполяции.
При использовании рациональных сплайнов путем надлежащего выбора свободных параметров , практически всегда удаётся одновременно удовлетворить требованиям и количественного и качественного характера, в том числе при интерполяции функций с большими градиентами. Данное обстоятельство делает рациональные сплайны фактически универсальным средством приближения функций.
Рассмотрим интерполяцию функции
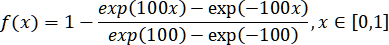
на сетке с узлами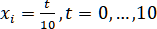 в качестве численного примера, демонстрирующего возможности рациональных сплайнов.
в качестве численного примера, демонстрирующего возможности рациональных сплайнов.
На рисунке 1.3 изображены графики интерполяционных сплайнов – кубического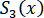 и рационального
и рационального  . Оба сплайна удовлетворяют граничным условиям типа
. Оба сплайна удовлетворяют граничным условиям типа
I.
II.
III. Условия периодичности:
IV.
где
Можно заметить, что первые три типа условий одинаковы по форме и содержанию с подобными условиями для кубических сплайнов. Содержание условий типа IV раскроем в алгоритме.
1.6 Алгоритм построения интерполяционного рационального сплайна
Из условий интерполяции получим
Подставив эти выражения для , в (1.5.1), получим
Сплайн (1.5.3) непрерывен в узлах сетки и удовлетворяет условиям (1.5.2). Определим коэффициенты так, чтобы были непрерывны его первая и вторая производные.
Если
то
Обозначив
Формулы (1.5.5) являются следствием непрерывности
Значит,
и условие непрерывности
Подставляя сюда и из (1.5.5), получим
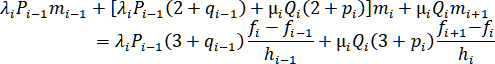
где
Выпишем системы уравнений относительно неизвестных для каждого вида краевых условий.
Типы I и II.
где для типа I:
для типа II:
Тип III:
причём
(1.5.7)
Тип IV:
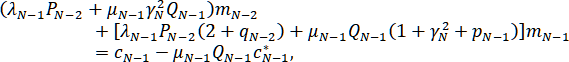
Матрицы всех полученных систем с диагональным преобладанием. Это открывает перспективы для их решения с помощью метода прогонки и гарантирует существование и единственность интерполяционного рационального сплайна
При
1.7. Периодический случай
на некотором промежутке
Теорема. Если A – матрица с диагональным преобладанием, то справедлива оценка
Используя данное следствие, из системы (1.5.7) получаем
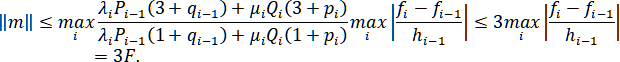
Из (1.5.5) получим
В частности, если для всех одновременно , то
Рациональные сплайны обладают свойствами наиболее часто встреча- ющихся на практике – сплайнов первой степени и кубических. Кубические сплайны показывают, чаще всего, высокую точность приближения гладких функций. Но при этом не всегда получается удовлетворить требованиям качественного характера. К примеру, если интерполируемая функция выпукла, то в некоторых случаях необходимо, чтобы и сплайн был выпуклым. Кубический
сплайн удовлетворяет этому требованию далеко не
всегда. Сплайн же первой степени в данной ситуации тоже будет выпуклым, но не всегда возможно получить необходимую точность приближения. Кроме всего прочего, сплайн первой степени не является гладкой функцией. Значимые проблемы могут возникнуть при приближении функции с большими градиентами. Использование в данном случае как кубических сплайнов, так и сплайнов первой степени, обычно связано с большим количеством узлов интерполяции.
При использовании рациональных сплайнов путем надлежащего выбора свободных параметров , практически всегда удаётся одновременно удовлетворить требованиям и количественного и качественного характера, в том числе при интерполяции функций с большими градиентами. Данное обстоятельство делает рациональные сплайны фактически универсальным средством приближения функций.
Рассмотрим интерполяцию функции
на сетке с узлами
На рисунке 1.3 изображены графики интерполяционных сплайнов – кубического