ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 413
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
FPM-04 универсальды маятнигі
Қысқаша теориялық мағлұмат
Жерге қатысты еркін түсу үдеуі жер шарыныңәр түрлі нүктелерінде әртүрлі. Сондықтан жер шарыныңәр түрлі нүктелерінде еркін түсу үдеуін анықтау бір жағынан жердің формасына нұсқау берсе екінші жағынан жер шарыныңқұрылымыныңәр түрлі жерлерінің бір текті еместігін бұзуға негізделеді.
Еркін түсу үдеуін анықтаудың дәл әдістерінің бірі маятниктердің тербелісін зерттеуге негізделген.
Физикада маятник деп қозғалмайтын оске қатысты ауырлық күшініңәсерінен тербелмелі қозғалыс жасайтын қатты денені айтады. Математикалық және физикалық маятниктер бар. Математикалық маятник деп салмақсыз және өте жіңішке созылмайтын жіпке ілінген массасы бір нүктеге жинақталған денеден тұратын идеал системаны айтады. Ұзын жіңішке жіпке ілінген өлшемі кішкентай ауыр шарикті математикалық маятник деп қарастыруға болады (1-сурет). С ауырлық центірінен жоғары орналасқан О нүктесі арқылы өтетін горизанталь оське бекітілген қатты денені физикалық маятник деп атайды. (2-сурет)
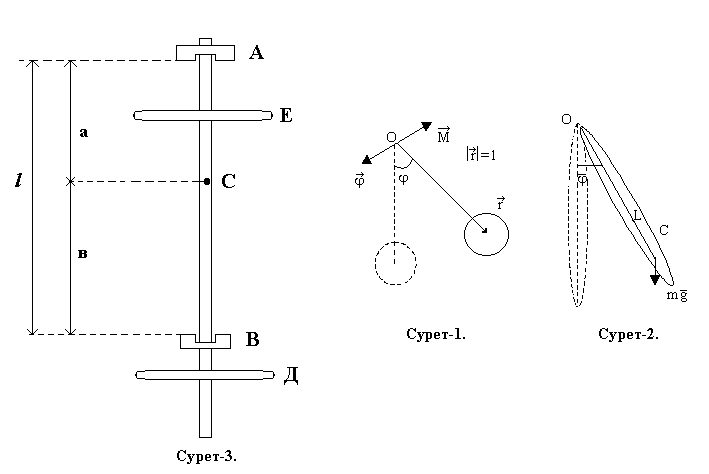
Осы маятниктердің қозғалыс динамикасын қарастырайық. Маятникті тепе-теңдіктен φ бұрышқа ауытқытқанда О нүктесіне қатысты айналдырушы ауырлық күшінің М моменті пайда болады. Осы берілген жағдайда денеге тек ауырлық күш моменті ғана әсер етеді, ал остің реакция күш моменті нөлге тең. Ауырлық күш моментінің қосындысы mg тең әсерлі күш моментіне тең екендігі белгілі және осы шарт кезінде ауырлық центіріне қарай ығысады. Бір текті өрісте ауырлық центірі дененің масса центірімен сәйкес келеді. Анықтама бойынша F күшінің О нүктесіне қатысты моменті
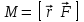
Мұндағы rО нүктесінен күш түсірілген жерге дейін жүргізілген радиус вектор. Қозғалмайтын оске қатысты дененің қозғалыс теңдеуі бұл айналмалы қозғалыс динамикасының негізгі теңдеуі болып табылады, және төмендегі түрде беріледі.
Айналмалы қозғалыс тыңнегізгі теңдеуі:
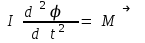(1) немесе M = I · ε (1!)
Мұндағы J – дененің айналыс осіне қатысты инерция моменті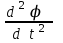
бұрыштық үдеуі.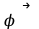
векторы айналыс осі бойынша жататын модулі 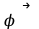-ге тең, бағыты бұрғы ережесі бойынша анықталған вектор. Векторды көбейту ережесі бойынша қарастырып отырған қозғалыс жағдайында ауырлық күшінің моменті 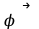векторынақарама-қарсы бағытталған. (1) дифференциалды теңдеуді шешу үшін 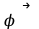үшін векторлық формадан скаляр түрге келтірейік. Ол үшін координата осін айналыс осі бойынша 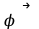- векторымен бағыттап, 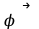және
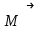векторларының осы оске проекциясын ескеріп, (1) теңдеуді проекциясы бойынша жазсақ, төмендегі түрге келеді:
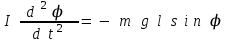(2)
жәнеM=[ rmg ] = lmgsinφ мұндағы ℓ= | r|,мұндағы (-) таңбасы М-нің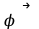 -ға қарама – қарсы бағытталғандығын білдіреді. Егер тепе-теңдіктен ауытқыту шамасы аз болғанда, яғни sinj»j онда (2) теңдеу былай жазылады.
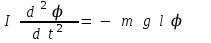(3)
немесе
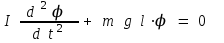(4)
(4) теңдеудің екі жағын І-ға бөліп, гармониялық тербелісті сипаттайтын теңдеу аламыз:
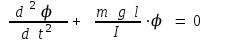(5)
Бұл дифференциалды теңдеудің жалпы шешімі:
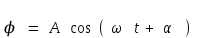(6)
Түрінде болады. Бұл жердеА, α – бастапқы шарттардан анықталатын тұрақтылар, ал
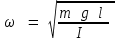- тербелістің циклдік жиілігі, ал біз тербеліс периоды мен циклдік жиілік арасында мынадай байланыс бар екенін білеміз, w=2p/T онда қарастырып отырған гармониялық тербеліс периоды мынаған тең:
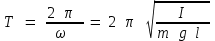(7)
осы (7) теңдеуді пайдаланып еркін түсу удеуін анықтайтын өрнекті жазуға болады:
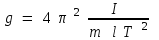(8)
Осылайша маятниктің тербеліс периодын және инерция моментін біле отырып, еркін түсу удеуін анықтауға болады, ал математикалық маятниктің инерция моменті
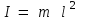
Олай болса, математикалық маятниктің көмегімен еркін түсу үдеуі төмендегі (9) өрнекпен сипатталады:
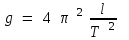(9)
(9) формуланы пайдаланып математикалық маятниктің тербелісін зерттеп, яғни тербеліс периодын өлшеп еркін түсу удеуін анықтауға болады.
Физикалық маятниктің көмегімен еркін түсу үдеуін анықтауға өзіндік қиындықтар болады.
Бұл жұмыста қарапайым физикалық маятник болып есептелетін айналмалы маятниктің көмегімен еркін түсу үдеуін анықтау қарастырылды. Айналмалы маятник (3-сурет) ұзынцилиндірілікбіліктентұрады. БіліккеекіА, В, қозғалмалыпризмалар және Е, Д ауырдискілерорнатылған. МаятниктіңА және Впризмалараралығыlболсын. А және Впризмаларарқылыөтетіностергеқатыстымаятниктіңтербеліспериодтарын ТА және ТВдейміз. (7) формулаға сәйкес.
(10)
бұл жерде -IA, IBА және В призмалары арқылы өтетін маятниктің инерция моменттері.
(10) теңдеудіңәрайсысын квадраттап, біріншісін а -ға, екіншісін в -ға көбейтіп, бірінен екіншісін алсақ мына өрнек шығады.
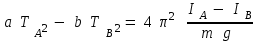(11)
IA, IB инерция моменттерін Штейнер теоремасы бойынша анықтаймыз, яғни
(12)
мұндағы айналмалы маятниктің ауырлық центрі арқылы өтетін оське қатысты инерция моменті (12) өрнектерді (11)-ге апарып қойсақ, онда еркін түсу үдеуі төмендегідей болады:
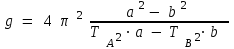(13)
Егер Е және Д дискілерін жылжыта отырып ТА=ТВ=Т орындалатындай етіп орналастырсақ, онда бұл жағдай үшін (13) формула мына түрге келген болар еді.
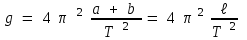(14)
Осы соңғы (14) өрнек айналмалы маятник үшін еркін түсу үдеуін анықтайтын жұмыс формуласы болып табылады.
Қондырғының түсіндірмесі
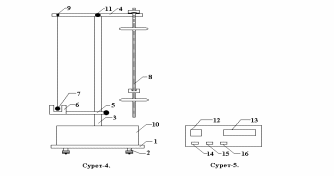
Универсал FPM – 04 маятниктің жалпы түрі 4-суретте көрсетілген. (1)- негіз (2) орнықтылық бұрандалары. (3) негізгі тіктеуіш (4) жоғарғы және (5) төменгі кронштейндер, (6) фотоэлектрлік санағыш орналасқан. (4) кронштейннің бір жағында (7) математикалық ал екінші жағында (8) айналмалы маятник орналасқан. Математикалық маятниктіңұзындығын (9) бұранда арқылы өзгертуге, ал оның шамасын (3) тік тіреуіштегі шкала бойынша білуге болады. Айналмалы маятниктің болат стержні ( білігі) бірінен бірі 10 мм қашықтықта болатын дөңгелек кесінділермен бөлінген. Төменгі кронштейін фотоэлектрлік санағышпен бірге оңай қозғалады. 5-суретте милисекундомер көрсетілген, ондағы (12) таблода период, яғни тербеліс саны, (13) таблода толық уақыт көрсетіледі.
Математикалық маятник көмегімен еркін түсу үдеуін анықтау
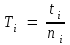
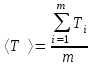
формуласымен есептейсіз, мұндағы m-тәжірибе саны
Бақылау сұрақтары
Әдебиеттер
№4 зертханалық жұмыс
Ауырлық күшінің үдеуін физикалық
маятниктің көмегімен анықтау
Жұмыстың мақсаты: Маятниктердің тербелісін зерттеу. Еркін түсу үдеуін анықтау.
Қажетті құрал-жабдықтар: FPM-04 универсальды маятнигі
Қысқаша теориялық мағлұмат
Жерге қатысты еркін түсу үдеуі жер шарыныңәр түрлі нүктелерінде әртүрлі. Сондықтан жер шарыныңәр түрлі нүктелерінде еркін түсу үдеуін анықтау бір жағынан жердің формасына нұсқау берсе екінші жағынан жер шарыныңқұрылымыныңәр түрлі жерлерінің бір текті еместігін бұзуға негізделеді.
Еркін түсу үдеуін анықтаудың дәл әдістерінің бірі маятниктердің тербелісін зерттеуге негізделген.
Физикада маятник деп қозғалмайтын оске қатысты ауырлық күшініңәсерінен тербелмелі қозғалыс жасайтын қатты денені айтады. Математикалық және физикалық маятниктер бар. Математикалық маятник деп салмақсыз және өте жіңішке созылмайтын жіпке ілінген массасы бір нүктеге жинақталған денеден тұратын идеал системаны айтады. Ұзын жіңішке жіпке ілінген өлшемі кішкентай ауыр шарикті математикалық маятник деп қарастыруға болады (1-сурет). С ауырлық центірінен жоғары орналасқан О нүктесі арқылы өтетін горизанталь оське бекітілген қатты денені физикалық маятник деп атайды. (2-сурет)
Осы маятниктердің қозғалыс динамикасын қарастырайық. Маятникті тепе-теңдіктен φ бұрышқа ауытқытқанда О нүктесіне қатысты айналдырушы ауырлық күшінің М моменті пайда болады. Осы берілген жағдайда денеге тек ауырлық күш моменті ғана әсер етеді, ал остің реакция күш моменті нөлге тең. Ауырлық күш моментінің қосындысы mg тең әсерлі күш моментіне тең екендігі белгілі және осы шарт кезінде ауырлық центіріне қарай ығысады. Бір текті өрісте ауырлық центірі дененің масса центірімен сәйкес келеді. Анықтама бойынша F күшінің О нүктесіне қатысты моменті
Мұндағы rО нүктесінен күш түсірілген жерге дейін жүргізілген радиус вектор. Қозғалмайтын оске қатысты дененің қозғалыс теңдеуі бұл айналмалы қозғалыс динамикасының негізгі теңдеуі болып табылады, және төмендегі түрде беріледі.
Айналмалы қозғалыс тыңнегізгі теңдеуі:
(1) немесе M = I · ε (1!)
Мұндағы J – дененің айналыс осіне қатысты инерция моменті
бұрыштық үдеуі. 
векторы айналыс осі бойынша жататын модулі -ге тең, бағыты бұрғы ережесі бойынша анықталған вектор. Векторды көбейту ережесі бойынша қарастырып отырған қозғалыс жағдайында ауырлық күшінің моменті
Қысқаша теориялық мағлұмат
Жерге қатысты еркін түсу үдеуі жер шарыныңәр түрлі нүктелерінде әртүрлі. Сондықтан жер шарыныңәр түрлі нүктелерінде еркін түсу үдеуін анықтау бір жағынан жердің формасына нұсқау берсе екінші жағынан жер шарыныңқұрылымыныңәр түрлі жерлерінің бір текті еместігін бұзуға негізделеді.
Еркін түсу үдеуін анықтаудың дәл әдістерінің бірі маятниктердің тербелісін зерттеуге негізделген.
Физикада маятник деп қозғалмайтын оске қатысты ауырлық күшініңәсерінен тербелмелі қозғалыс жасайтын қатты денені айтады. Математикалық және физикалық маятниктер бар. Математикалық маятник деп салмақсыз және өте жіңішке созылмайтын жіпке ілінген массасы бір нүктеге жинақталған денеден тұратын идеал системаны айтады. Ұзын жіңішке жіпке ілінген өлшемі кішкентай ауыр шарикті математикалық маятник деп қарастыруға болады (1-сурет). С ауырлық центірінен жоғары орналасқан О нүктесі арқылы өтетін горизанталь оське бекітілген қатты денені физикалық маятник деп атайды. (2-сурет)
Осы маятниктердің қозғалыс динамикасын қарастырайық. Маятникті тепе-теңдіктен φ бұрышқа ауытқытқанда О нүктесіне қатысты айналдырушы ауырлық күшінің М моменті пайда болады. Осы берілген жағдайда денеге тек ауырлық күш моменті ғана әсер етеді, ал остің реакция күш моменті нөлге тең. Ауырлық күш моментінің қосындысы mg тең әсерлі күш моментіне тең екендігі белгілі және осы шарт кезінде ауырлық центіріне қарай ығысады. Бір текті өрісте ауырлық центірі дененің масса центірімен сәйкес келеді. Анықтама бойынша F күшінің О нүктесіне қатысты моменті
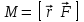
Мұндағы rО нүктесінен күш түсірілген жерге дейін жүргізілген радиус вектор. Қозғалмайтын оске қатысты дененің қозғалыс теңдеуі бұл айналмалы қозғалыс динамикасының негізгі теңдеуі болып табылады, және төмендегі түрде беріледі.
Айналмалы қозғалыс тыңнегізгі теңдеуі:
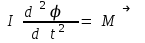(1) немесе M = I · ε (1!) Мұндағы J – дененің айналыс осіне қатысты инерция моменті
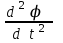
бұрыштық үдеуі.
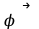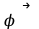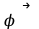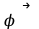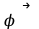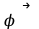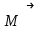векторы айналыс осі бойынша жататын модулі -ге тең, бағыты бұрғы ережесі бойынша анықталған вектор. Векторды көбейту ережесі бойынша қарастырып отырған қозғалыс жағдайында ауырлық күшінің моменті векторынақарама-қарсы бағытталған. (1) дифференциалды теңдеуді шешу үшін үшін векторлық формадан скаляр түрге келтірейік. Ол үшін координата осін айналыс осі бойынша - векторымен бағыттап, және векторларының осы оске проекциясын ескеріп, (1) теңдеуді проекциясы бойынша жазсақ, төмендегі түрге келеді: 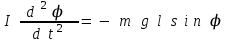(2)жәнеM=[ rmg ] = lmgsinφ мұндағы ℓ= | r|,мұндағы (-) таңбасы М-нің
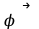-ға қарама – қарсы бағытталғандығын білдіреді. Егер тепе-теңдіктен ауытқыту шамасы аз болғанда, яғни sinj»j онда (2) теңдеу былай жазылады. 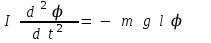(3)немесе
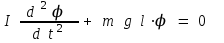(4)(4) теңдеудің екі жағын І-ға бөліп, гармониялық тербелісті сипаттайтын теңдеу аламыз:
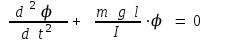(5)Бұл дифференциалды теңдеудің жалпы шешімі:
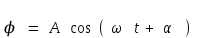(6)Түрінде болады. Бұл жердеА, α – бастапқы шарттардан анықталатын тұрақтылар, ал
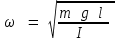- тербелістің циклдік жиілігі, ал біз тербеліс периоды мен циклдік жиілік арасында мынадай байланыс бар екенін білеміз, w=2p/T онда қарастырып отырған гармониялық тербеліс периоды мынаған тең: 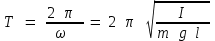(7)осы (7) теңдеуді пайдаланып еркін түсу удеуін анықтайтын өрнекті жазуға болады:
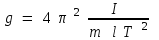(8)Осылайша маятниктің тербеліс периодын және инерция моментін біле отырып, еркін түсу удеуін анықтауға болады, ал математикалық маятниктің инерция моменті
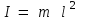
Олай болса, математикалық маятниктің көмегімен еркін түсу үдеуі төмендегі (9) өрнекпен сипатталады:
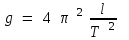(9)(9) формуланы пайдаланып математикалық маятниктің тербелісін зерттеп, яғни тербеліс периодын өлшеп еркін түсу удеуін анықтауға болады.
Физикалық маятниктің көмегімен еркін түсу үдеуін анықтауға өзіндік қиындықтар болады.
Бұл жұмыста қарапайым физикалық маятник болып есептелетін айналмалы маятниктің көмегімен еркін түсу үдеуін анықтау қарастырылды. Айналмалы маятник (3-сурет) ұзынцилиндірілікбіліктентұрады. БіліккеекіА, В, қозғалмалыпризмалар және Е, Д ауырдискілерорнатылған. МаятниктіңА және Впризмалараралығыlболсын. А және Впризмаларарқылыөтетіностергеқатыстымаятниктіңтербеліспериодтарын ТА және ТВдейміз. (7) формулаға сәйкес.
(10)бұл жерде -IA, IBА және В призмалары арқылы өтетін маятниктің инерция моменттері.
(10) теңдеудіңәрайсысын квадраттап, біріншісін а -ға, екіншісін в -ға көбейтіп, бірінен екіншісін алсақ мына өрнек шығады.
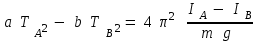(11) IA, IB инерция моменттерін Штейнер теоремасы бойынша анықтаймыз, яғни
(12)мұндағы айналмалы маятниктің ауырлық центрі арқылы өтетін оське қатысты инерция моменті (12) өрнектерді (11)-ге апарып қойсақ, онда еркін түсу үдеуі төмендегідей болады:
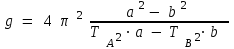(13)Егер Е және Д дискілерін жылжыта отырып ТА=ТВ=Т орындалатындай етіп орналастырсақ, онда бұл жағдай үшін (13) формула мына түрге келген болар еді.
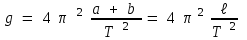(14)Осы соңғы (14) өрнек айналмалы маятник үшін еркін түсу үдеуін анықтайтын жұмыс формуласы болып табылады.
Қондырғының түсіндірмесі
Универсал FPM – 04 маятниктің жалпы түрі 4-суретте көрсетілген. (1)- негіз (2) орнықтылық бұрандалары. (3) негізгі тіктеуіш (4) жоғарғы және (5) төменгі кронштейндер, (6) фотоэлектрлік санағыш орналасқан. (4) кронштейннің бір жағында (7) математикалық ал екінші жағында (8) айналмалы маятник орналасқан. Математикалық маятниктіңұзындығын (9) бұранда арқылы өзгертуге, ал оның шамасын (3) тік тіреуіштегі шкала бойынша білуге болады. Айналмалы маятниктің болат стержні ( білігі) бірінен бірі 10 мм қашықтықта болатын дөңгелек кесінділермен бөлінген. Төменгі кронштейін фотоэлектрлік санағышпен бірге оңай қозғалады. 5-суретте милисекундомер көрсетілген, ондағы (12) таблода период, яғни тербеліс саны, (13) таблода толық уақыт көрсетіледі.
Математикалық маятник көмегімен еркін түсу үдеуін анықтау
-
Қондырғымен танысу, оны жұмысқа дайындау. -
Маятник 4-50 –қа тепе-теңдк жағдайдан ауытқыту және «сброс» клавишін басасыз. Маятниктің ұзындығы 50 см - ден асырмауыңыз қажет. -
(12) таблода 10 цифры жанғандакейін «стоп» клавишін басасыз. -
Таблицаға (13) таблодағы уақыттың (t) көрсетуін және осы уақытқа жасалған (n)тербеліс санын (12) таблоның көрсетуі бойынша жазасыз. -
«Сброс» клавишін басып, өлшеуді жаңадан бастайсыз. Тәжірибе 10 шақты рет қайталануы қажет. -
Әрбір өлшем үшін математикалық маятниктің тербеліс периодын төмендегі формула бойынша анықтаймыз:
-
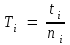
Тербеліс периодының орташа мәнін
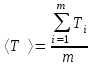
формуласымен есептейсіз, мұндағы m-тәжірибе саны
-
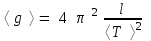осы жұмыс формуласы бойынша еркін түсу үдеуінің орташа мәнін анықтайсыз.
Бақылау сұрақтары
-
Еркін түсу үдеуі қандай факторларға тәуелді ? -
Математикалық және физикалық маятниктердің анықтамасы -
Штейнер теоремасын тұжырымда -
Математикалық маятниктің көмегімен еркін түсу үдеуін анықтайтын жұмыс формуласын қорытып шығар -
Физикалық маятниктердің көмегімен еркін түсу үдеуін анықтайтын жұмыс формуласын қорытып шығар
Әдебиеттер
-
И.В Савельев. Жалпы физика курсы, 1 том, М; Наука, 1977 -
Хайкин С.Э. Физические основы механики. М: Наука 1971 -
Сивухин Д.В. Общий курс физики Том 1 М: Механика, 1979 -
Китаева Л.П. Рекомендации по оценке погрешности для студентов І и ІІ курсов. Томск, 1983
№4 зертханалық жұмыс
Ауырлық күшінің үдеуін физикалық
маятниктің көмегімен анықтау
Жұмыстың мақсаты: Маятниктердің тербелісін зерттеу. Еркін түсу үдеуін анықтау.
Қажетті құрал-жабдықтар: FPM-04 универсальды маятнигі
Қысқаша теориялық мағлұмат
Жерге қатысты еркін түсу үдеуі жер шарыныңәр түрлі нүктелерінде әртүрлі. Сондықтан жер шарыныңәр түрлі нүктелерінде еркін түсу үдеуін анықтау бір жағынан жердің формасына нұсқау берсе екінші жағынан жер шарыныңқұрылымыныңәр түрлі жерлерінің бір текті еместігін бұзуға негізделеді.
Еркін түсу үдеуін анықтаудың дәл әдістерінің бірі маятниктердің тербелісін зерттеуге негізделген.
Физикада маятник деп қозғалмайтын оске қатысты ауырлық күшініңәсерінен тербелмелі қозғалыс жасайтын қатты денені айтады. Математикалық және физикалық маятниктер бар. Математикалық маятник деп салмақсыз және өте жіңішке созылмайтын жіпке ілінген массасы бір нүктеге жинақталған денеден тұратын идеал системаны айтады. Ұзын жіңішке жіпке ілінген өлшемі кішкентай ауыр шарикті математикалық маятник деп қарастыруға болады (1-сурет). С ауырлық центірінен жоғары орналасқан О нүктесі арқылы өтетін горизанталь оське бекітілген қатты денені физикалық маятник деп атайды. (2-сурет)
Осы маятниктердің қозғалыс динамикасын қарастырайық. Маятникті тепе-теңдіктен φ бұрышқа ауытқытқанда О нүктесіне қатысты айналдырушы ауырлық күшінің М моменті пайда болады. Осы берілген жағдайда денеге тек ауырлық күш моменті ғана әсер етеді, ал остің реакция күш моменті нөлге тең. Ауырлық күш моментінің қосындысы mg тең әсерлі күш моментіне тең екендігі белгілі және осы шарт кезінде ауырлық центіріне қарай ығысады. Бір текті өрісте ауырлық центірі дененің масса центірімен сәйкес келеді. Анықтама бойынша F күшінің О нүктесіне қатысты моменті
Мұндағы rО нүктесінен күш түсірілген жерге дейін жүргізілген радиус вектор. Қозғалмайтын оске қатысты дененің қозғалыс теңдеуі бұл айналмалы қозғалыс динамикасының негізгі теңдеуі болып табылады, және төмендегі түрде беріледі.
Айналмалы қозғалыс тыңнегізгі теңдеуі:
(1) немесе M = I · ε (1!) Мұндағы J – дененің айналыс осіне қатысты инерция моменті
бұрыштық үдеуі. векторы айналыс осі бойынша жататын модулі -ге тең, бағыты бұрғы ережесі бойынша анықталған вектор. Векторды көбейту ережесі бойынша қарастырып отырған қозғалыс жағдайында ауырлық күшінің моменті