ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 414
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
векторынақарама-қарсы бағытталған. (1) дифференциалды теңдеуді шешу үшін 
үшін векторлық формадан скаляр түрге келтірейік. Ол үшін координата осін айналыс осі бойынша - векторымен бағыттап, және
векторларының осы оске проекциясын ескеріп, (1) теңдеуді проекциясы бойынша жазсақ, төмендегі түрге келеді:
(2)
жәнеM=[ rmg ] = lmgsinφ мұндағы ℓ= | r|,мұндағы (-) таңбасы М-нің -ға қарама – қарсы бағытталғандығын білдіреді. Егер тепе-теңдіктен ауытқыту шамасы аз болғанда, яғни sinj»j онда (2) теңдеу былай жазылады.
(3)
немесе
(4)
(4) теңдеудің екі жағын І-ға бөліп, гармониялық тербелісті сипаттайтын теңдеу аламыз:
(5)
Бұл дифференциалды теңдеудің жалпы шешімі:
(6)
Түрінде болады. Бұл жердеА, α – бастапқы шарттардан анықталатын тұрақтылар, ал
- тербелістің циклдік жиілігі, ал біз тербеліс периоды мен циклдік жиілік арасында мынадай байланыс бар екенін білеміз, w=2p/T онда қарастырып отырған гармониялық тербеліс периоды мынаған тең:
(7)
осы (7) теңдеуді пайдаланып еркін түсу удеуін анықтайтын өрнекті жазуға болады:
(8)
Осылайша маятниктің тербеліс периодын және инерция моментін біле отырып, еркін түсу удеуін анықтауға болады, ал математикалық маятниктің инерция моменті
Олай болса, математикалық маятниктің көмегімен еркін түсу үдеуі төмендегі (9) өрнекпен сипатталады:
(9)
(9) формуланы пайдаланып математикалық маятниктің тербелісін зерттеп, яғни тербеліс периодын өлшеп еркін түсу удеуін анықтауға болады.
Физикалық маятниктің көмегімен еркін түсу үдеуін анықтауға өзіндік қиындықтар болады.
Бұл жұмыста қарапайым физикалық маятник болып есептелетін айналмалы маятниктің көмегімен еркін түсу үдеуін анықтау қарастырылды. Айналмалы маятник (3-сурет) ұзынцилиндірілікбіліктентұрады. БіліккеекіА, В, қозғалмалыпризмалар және Е, Д ауырдискілерорнатылған. МаятниктіңА және Впризмалараралығыlболсын. А және Впризмаларарқылыөтетіностергеқатыстымаятниктіңтербеліспериодтарын ТА және ТВдейміз. (7) формулаға сәйкес.
(10)
бұл жерде -IA, IBА және В призмалары арқылы өтетін маятниктің инерция моменттері.
(10) теңдеудіңәрайсысын квадраттап, біріншісін а -ға, екіншісін в -ға көбейтіп, бірінен екіншісін алсақ мына өрнек шығады.
(11)
IA, IB инерция моменттерін Штейнер теоремасы бойынша анықтаймыз, яғни
(12)
мұндағы айналмалы маятниктің ауырлық центрі арқылы өтетін оське қатысты инерция моменті (12) өрнектерді (11)-ге апарып қойсақ, онда еркін түсу үдеуі төмендегідей болады:
(13)
Егер Е және Д дискілерін жылжыта отырып ТА=ТВ=Т орындалатындай етіп орналастырсақ, онда бұл жағдай үшін (13) формула мына түрге келген болар еді.
(14)
Осы соңғы (14) өрнек айналмалы маятник үшін еркін түсу үдеуін анықтайтын жұмыс формуласы болып табылады.
Қондырғының түсіндірмесі
Универсал FPM – 04 маятниктің жалпы түрі 4-суретте көрсетілген. (1)- негіз (2) орнықтылық бұрандалары. (3) негізгі тіктеуіш (4) жоғарғы және (5) төменгі кронштейндер, (6) фотоэлектрлік санағыш орналасқан. (4) кронштейннің бір жағында (7) математикалық ал екінші жағында (8) айналмалы маятник орналасқан. Математикалық маятниктіңұзындығын (9) бұранда арқылы өзгертуге, ал оның шамасын (3) тік тіреуіштегі шкала бойынша білуге болады. Айналмалы маятниктің болат стержні ( білігі) бірінен бірі 10 мм қашықтықта болатын дөңгелек кесінділермен бөлінген. Төменгі кронштейін фотоэлектрлік санағышпен бірге оңай қозғалады. 5-суретте милисекундомер көрсетілген, ондағы (12) таблода период, яғни тербеліс саны, (13) таблода толық уақыт көрсетіледі.
Айналмалы маятниктің көмегімен еркін түсу үдеуін анықтау
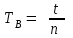
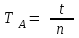-анықтау керек.
Бақылау сұрақтары
Әдебиеттер
№5 зертханалық жұмыс
Көлбеу маятниктің тербелісі бойынша домалау үйкеліс
коэффициентін анықтау
Жұмыстың мақсаты: Болат шардың Әртүрлі материалдардан жасалған жазық беттермен домалау үйкеліс коэффициентін тӘжірибемен анықтап, салыстырып талдау жасау.
Қажетті құрал-жабдықтар: FPM-04 Польша қондырғысы.
1 -сурет
R реакция күшінің нормаль құраушысының шамасы Rn=N, ал горизанталь құраушысы Rt= Fүйк домалау үйкеліс күшін береді.
Шар немесе цилиндр жазық бетпен үдеусіз қозғалса, моменттердің тепе-теңдік ережесі орындалуы қажет. Домалау үйкеліс күшінің О нүктесімен салыстырғандағы моменті Rn күшінің моментіне тең болады:
Fүйк r =Rn К (1)
М
ұндағы r –домалаған дененің радиусы, K - Rn күшінің иіні, деформацияланудан реакция күшінің Әсер ету нүктесінің ығысу аралығы. К – шамасын домалау үйкеліс күшінің коэффициенті деп атайды. Бұл жұмыста көлбеу маятник Әдісі қолданылып, шардың жазық бетпен домалау үйкеліс коэффициенті анықталады. Көлбеу маятник дегеніміз көлбеу бетке орналастырылған тербеліс жасай алатын математикалық маятник төмендегі 2-суретте көрсетілген.
2-сурет
Тепе – теңдік жағайдан j бұрышқа ауытқытылған осындай маятник шардың домалау үйкеліс Әсерінен өшетін тербеліс жасайды. Көлбеу маятник жағдайында ауырлық күшінің нормаль құраушысы:
N = mg cos b (2)
Домалау үйкеліс күші шардың жылдамдығына тӘуелді болмайды деп есептейміз ( Fүйк =const). Бұл жағдайда маятник амплитудасының кемуі арифметикалық прогрессия заңы бойынша өтеді.
Маятник n тербеліс жасап, С орнынан С1 орнына ауысқанда (3-сурет) оның энергиясының азаюы:
DЕ = mgDh
мұндағы Dh – шардың ауырлық центрінің биіктігінің өзгерісі.
Бұл энергия үйкеліс күштерінің маятниктің жүріп өткен жолдарында істеген жұмысына тең болады:
DЕ =DА + DА1 (3)
мұндағы DА=Fүйк S – домалау үйкеліс күшінің жұмысы, DА1-ортаның үйкеліс күшінің жұмысы, ол аз болғандықтан, оны ескермеуге болады.
Сондықтан:
mgDh = Fүйк S (4)
3-суреттен көрініп тұрғандай Dћ жӘне Dl шамалары арасындағы байланыс мына қатынаспен анықталады:
Dћ =Dlsin b (5)
(5), (1), (2) қатынастарды (4) теңдеуге апарып қойсақ:
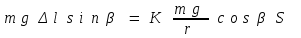(6)
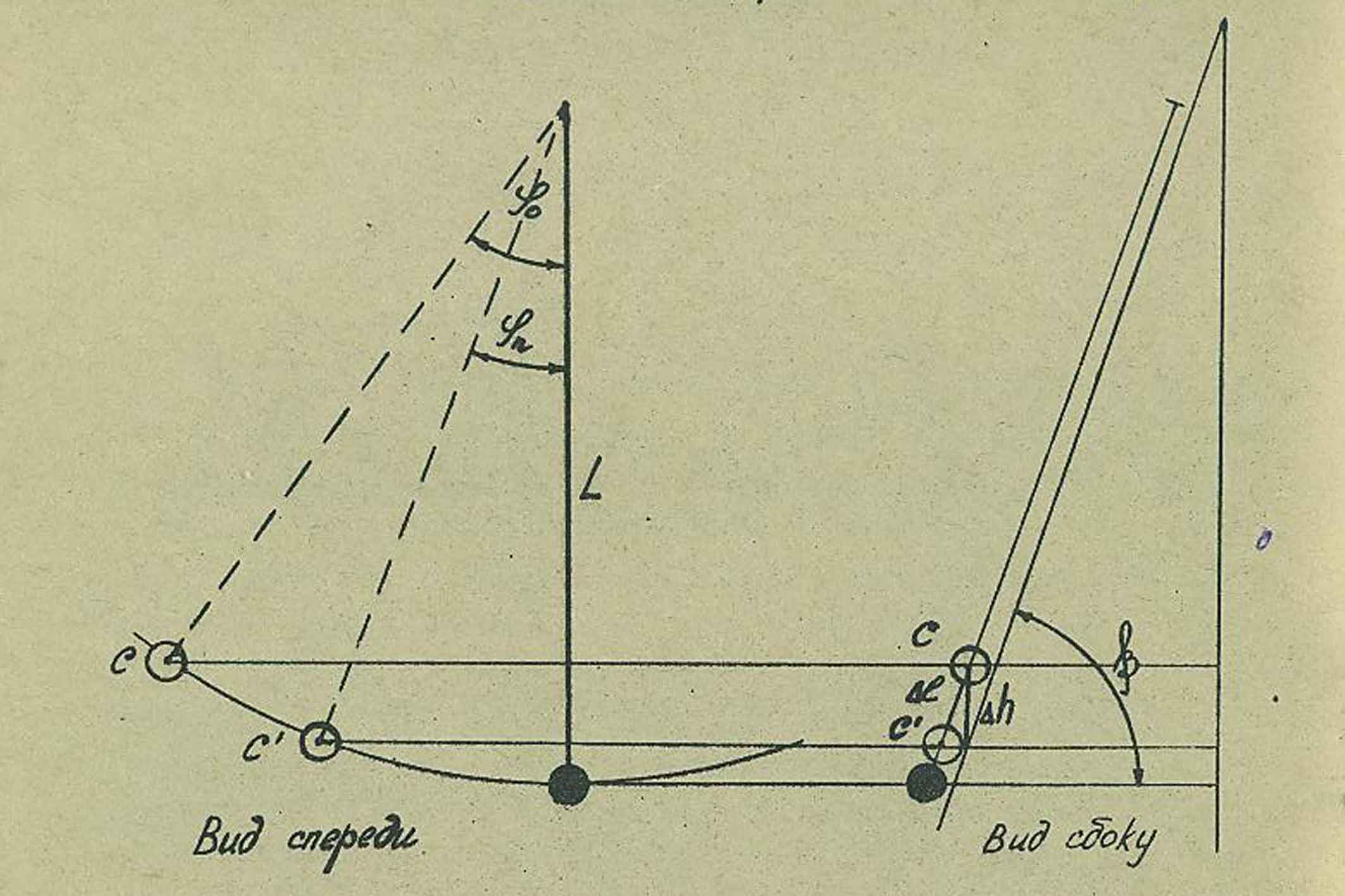
3- сурет
Маятниктің жүрген S жолын былайша есептейміз.
Бастапқы уақыт кезіндегі ауытқу бұрышы - j
0, n тербелістен кейінгі ауытқу бұрышы - jn, маятниктің ұзындығы – L болса (3-сурет), онда маятник шарының (ауырлық центрінің ) n тербеліс жасағанда, жүрген жолы :
S – маятник сызып өткен барлық доғалардың ұзындықтарының қосындысы. Доғаның ұзындығы оның радиусымен, олардың арасындағы бұрыштың көбейтіндісіне тең болады. Толық бір тербеліс кезінде маятник ұзындығы арифметикалық прогрессия бойынша кемитін, 4 рет доға сызып өтеді, сондықтан оның орташа мӘні:
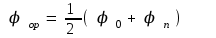(8)
(8), (7) ескеріп, (6) теңдеуден домалау үйкеліс коэффициентін анықтауға болады:
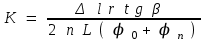(9)
3-суреттен көрінетіндей:
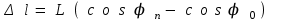
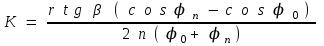(10)
Тәжірибеде ауытқу бұрыштарының мәні аз болғандықтан, үйкеліс коэффициентін есептеу үшін мына жуық формуланы қолданады:
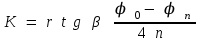(11)
Көлбеу бет прибордың негізімен мықтап бекітілген. Онда маятниктің тербеліс санын есептейтін фотоэлектрондық өлшеуіш бар. Беттің көлбеулік бұрышын жайлап өзгертуге болады. Маятниктің тепе-теңдік жағдайдан ауытқуы дәлдігі 30/ болатын шкала бойынша өлшенеді. Приборда бетімен шар домалайтын пластинаны оңай ауыстыруға болады. Өлшеу FPM қондырғысында жасалады.
үшін векторлық формадан скаляр түрге келтірейік. Ол үшін координата осін айналыс осі бойынша - векторымен бағыттап, және векторларының осы оске проекциясын ескеріп, (1) теңдеуді проекциясы бойынша жазсақ, төмендегі түрге келеді: (2)жәнеM=[ rmg ] = lmgsinφ мұндағы ℓ= | r|,мұндағы (-) таңбасы М-нің
-ға қарама – қарсы бағытталғандығын білдіреді. Егер тепе-теңдіктен ауытқыту шамасы аз болғанда, яғни sinj»j онда (2) теңдеу былай жазылады. (3)немесе
(4)(4) теңдеудің екі жағын І-ға бөліп, гармониялық тербелісті сипаттайтын теңдеу аламыз:
(5)Бұл дифференциалды теңдеудің жалпы шешімі:
(6)Түрінде болады. Бұл жердеА, α – бастапқы шарттардан анықталатын тұрақтылар, ал
- тербелістің циклдік жиілігі, ал біз тербеліс периоды мен циклдік жиілік арасында мынадай байланыс бар екенін білеміз, w=2p/T онда қарастырып отырған гармониялық тербеліс периоды мынаған тең: (7)осы (7) теңдеуді пайдаланып еркін түсу удеуін анықтайтын өрнекті жазуға болады:
(8)Осылайша маятниктің тербеліс периодын және инерция моментін біле отырып, еркін түсу удеуін анықтауға болады, ал математикалық маятниктің инерция моменті
Олай болса, математикалық маятниктің көмегімен еркін түсу үдеуі төмендегі (9) өрнекпен сипатталады:
(9)(9) формуланы пайдаланып математикалық маятниктің тербелісін зерттеп, яғни тербеліс периодын өлшеп еркін түсу удеуін анықтауға болады.
Физикалық маятниктің көмегімен еркін түсу үдеуін анықтауға өзіндік қиындықтар болады.
Бұл жұмыста қарапайым физикалық маятник болып есептелетін айналмалы маятниктің көмегімен еркін түсу үдеуін анықтау қарастырылды. Айналмалы маятник (3-сурет) ұзынцилиндірілікбіліктентұрады. БіліккеекіА, В, қозғалмалыпризмалар және Е, Д ауырдискілерорнатылған. МаятниктіңА және Впризмалараралығыlболсын. А және Впризмаларарқылыөтетіностергеқатыстымаятниктіңтербеліспериодтарын ТА және ТВдейміз. (7) формулаға сәйкес.
(10)бұл жерде -IA, IBА және В призмалары арқылы өтетін маятниктің инерция моменттері.
(10) теңдеудіңәрайсысын квадраттап, біріншісін а -ға, екіншісін в -ға көбейтіп, бірінен екіншісін алсақ мына өрнек шығады.
(11) IA, IB инерция моменттерін Штейнер теоремасы бойынша анықтаймыз, яғни
(12)мұндағы айналмалы маятниктің ауырлық центрі арқылы өтетін оське қатысты инерция моменті (12) өрнектерді (11)-ге апарып қойсақ, онда еркін түсу үдеуі төмендегідей болады:
(13)Егер Е және Д дискілерін жылжыта отырып ТА=ТВ=Т орындалатындай етіп орналастырсақ, онда бұл жағдай үшін (13) формула мына түрге келген болар еді.
(14)Осы соңғы (14) өрнек айналмалы маятник үшін еркін түсу үдеуін анықтайтын жұмыс формуласы болып табылады.
Қондырғының түсіндірмесі
Универсал FPM – 04 маятниктің жалпы түрі 4-суретте көрсетілген. (1)- негіз (2) орнықтылық бұрандалары. (3) негізгі тіктеуіш (4) жоғарғы және (5) төменгі кронштейндер, (6) фотоэлектрлік санағыш орналасқан. (4) кронштейннің бір жағында (7) математикалық ал екінші жағында (8) айналмалы маятник орналасқан. Математикалық маятниктіңұзындығын (9) бұранда арқылы өзгертуге, ал оның шамасын (3) тік тіреуіштегі шкала бойынша білуге болады. Айналмалы маятниктің болат стержні ( білігі) бірінен бірі 10 мм қашықтықта болатын дөңгелек кесінділермен бөлінген. Төменгі кронштейін фотоэлектрлік санағышпен бірге оңай қозғалады. 5-суретте милисекундомер көрсетілген, ондағы (12) таблода период, яғни тербеліс саны, (13) таблода толық уақыт көрсетіледі.
Айналмалы маятниктің көмегімен еркін түсу үдеуін анықтау
-
Айналмалы маятникті жұмысқа дайындау. -
Стерженнің шетіне жақын орналасқан Впризмасы арқылы маятникті жоғарғы кронштейнге орналастыруыңыз қажет. -
Төменгі кронштейнді фотоэлектрлік есептегішпен бірге маятниктің стержені тербеліс кезінде оның осін қиып өтетіндей етіп орналастырыңыз. -
Маятникті 4-50 –қа тепе-теңдік жағдайынан ауытқытыңыз. -
Сброс клавишін басуыңыз керек. -
10 тербеліс жасағаннан кейін «Стоп» клавишін басуыңыз керек. -
Тербеліс периодын есептеу:
-
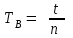
Маятникті А призмасы арқылы орналастыру. -
3,4,5,6-пункттреді қайталап
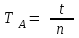-анықтау керек.-
Айналмалы маятниктің lұзындығын ТА=TВ=T жағдайы үшін призмалардың аралығын есептеп табасыз. -
(14) формула бойынша еркін түсу үдеуін есептеп, өлшеу қателігін бағалауыңыз керек.
Бақылау сұрақтары
-
Еркін түсу үдеуі қандай факторларға тәуелді ? -
Математикалық және физикалық маятниктердің анықтамасы -
Штейнер теоремасын тұжырымда -
Математикалық маятниктің көмегімен еркін түсу үдеуін анықтайтын жұмыс формуласын қорытып шығар -
Физикалық маятниктердің көмегімен еркін түсу үдеуін анықтайтын жұмыс формуласын қорытып шығар
Әдебиеттер
-
И.В Савельев. Жалпы физика курсы, 1 том, М; Наука, 1977 -
Хайкин С.Э. Физические основы механики. М: Наука 1971 -
Сивухин Д.В. Общий курс физики Том 1 М: Механика, 1979 -
Китаева Л.П. Рекомендации по оценке погрешности для студентов І и ІІ курсов. Томск, 1983
№5 зертханалық жұмыс
Көлбеу маятниктің тербелісі бойынша домалау үйкеліс
коэффициентін анықтау
Жұмыстың мақсаты: Болат шардың Әртүрлі материалдардан жасалған жазық беттермен домалау үйкеліс коэффициентін тӘжірибемен анықтап, салыстырып талдау жасау.
Қажетті құрал-жабдықтар: FPM-04 Польша қондырғысы.
Қысқаша теориялық мағлұмат
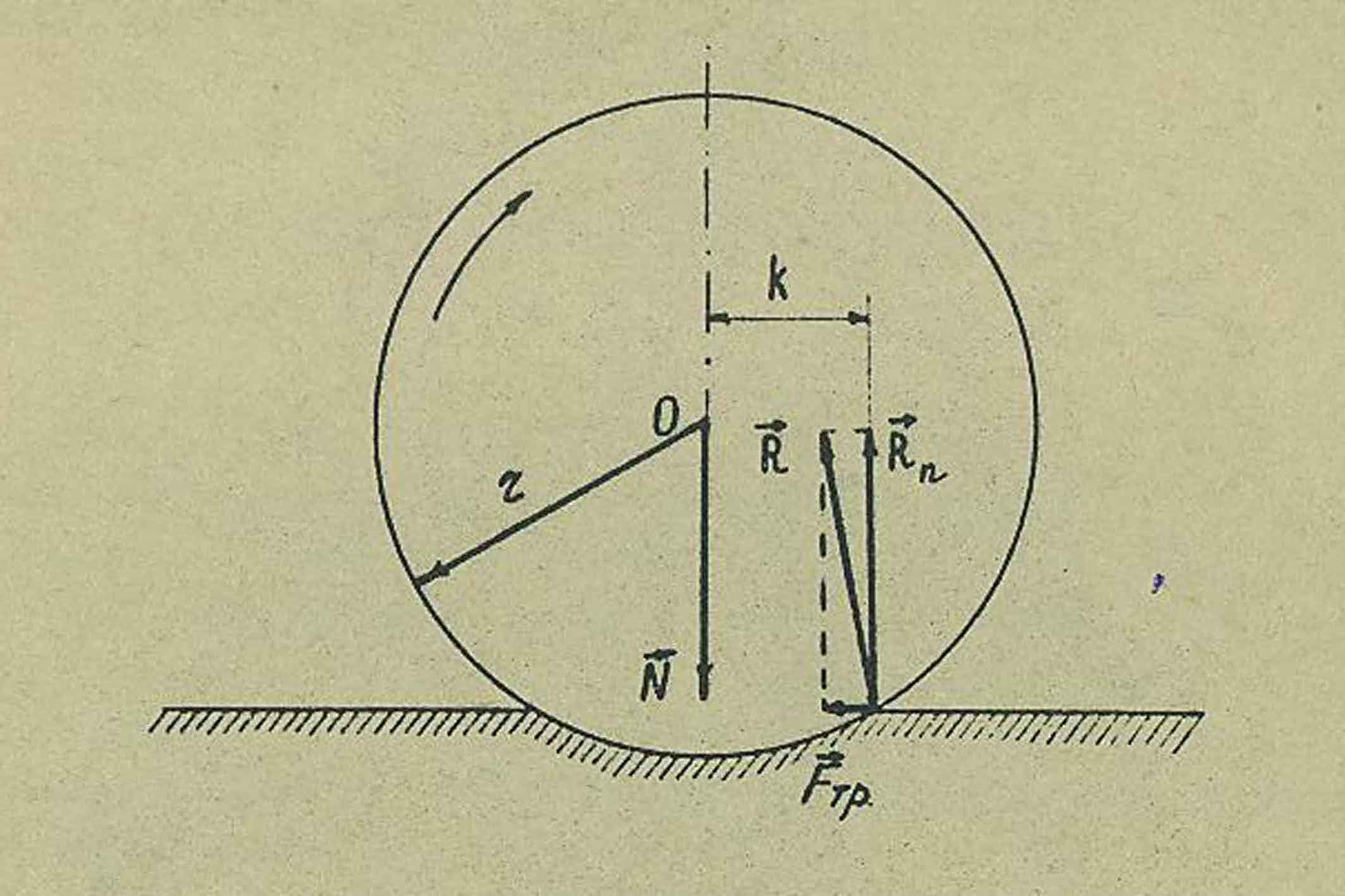
Шар немесе цилиндр формалы денелер жазық бетпен домалаған кезде бетпен дененің тиіскен жерлері деформацияланады. Деформация кезіндегі денелердің молекулаларының Әсерлесуі нӘтижесінде үйкеліс пайда болады. Деформацияның пайда болуынан жазық беттің реакция күшінің R Әсер сызығы нормаль қысым күшінің N Әсер сызығымене дӘл келмейді.
1 -сурет
R реакция күшінің нормаль құраушысының шамасы Rn=N, ал горизанталь құраушысы Rt= Fүйк домалау үйкеліс күшін береді.
Шар немесе цилиндр жазық бетпен үдеусіз қозғалса, моменттердің тепе-теңдік ережесі орындалуы қажет. Домалау үйкеліс күшінің О нүктесімен салыстырғандағы моменті Rn күшінің моментіне тең болады:
Fүйк r =Rn К (1)
М
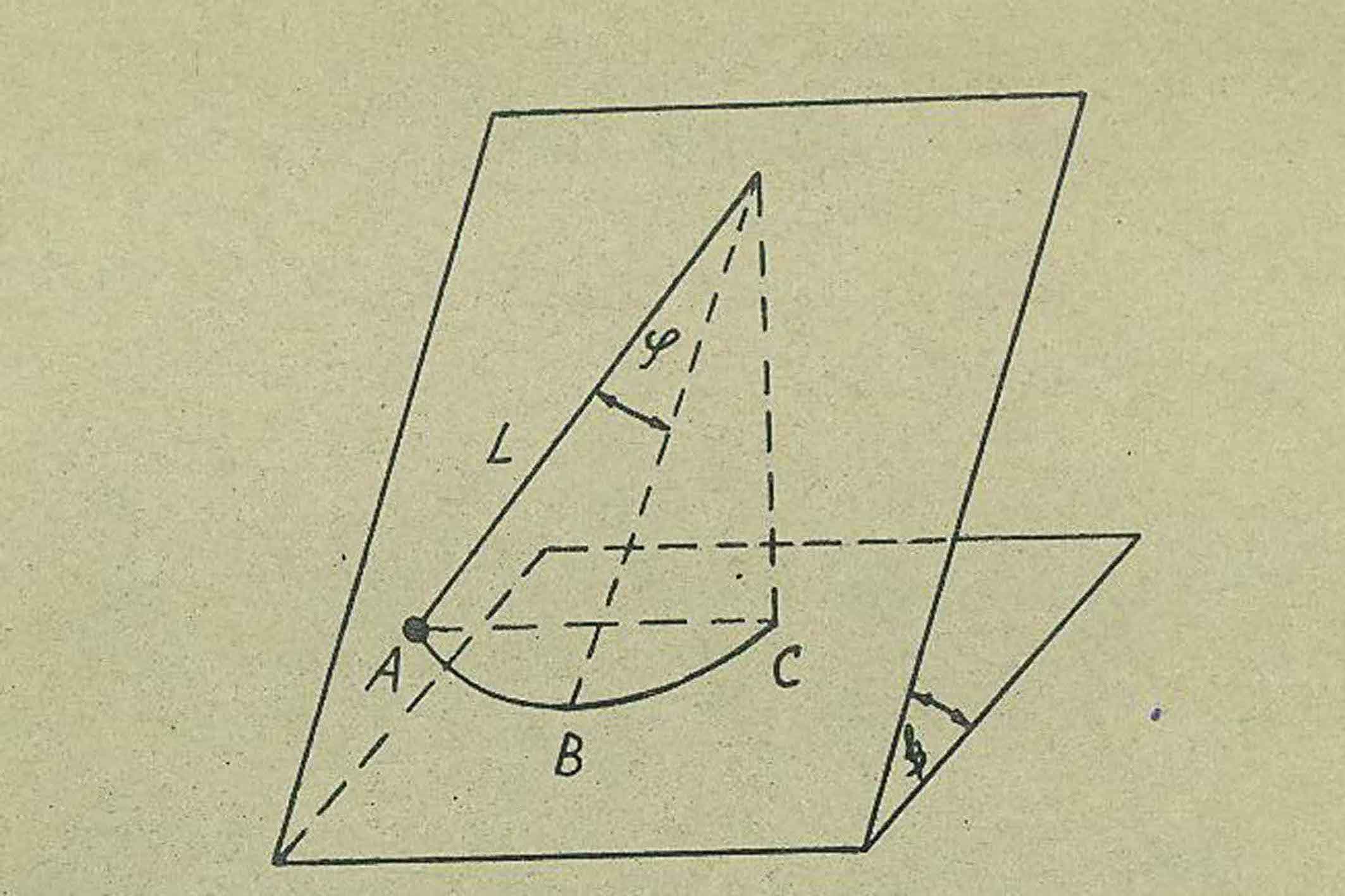
ұндағы r –домалаған дененің радиусы, K - Rn күшінің иіні, деформацияланудан реакция күшінің Әсер ету нүктесінің ығысу аралығы. К – шамасын домалау үйкеліс күшінің коэффициенті деп атайды. Бұл жұмыста көлбеу маятник Әдісі қолданылып, шардың жазық бетпен домалау үйкеліс коэффициенті анықталады. Көлбеу маятник дегеніміз көлбеу бетке орналастырылған тербеліс жасай алатын математикалық маятник төмендегі 2-суретте көрсетілген.
2-сурет
Тепе – теңдік жағайдан j бұрышқа ауытқытылған осындай маятник шардың домалау үйкеліс Әсерінен өшетін тербеліс жасайды. Көлбеу маятник жағдайында ауырлық күшінің нормаль құраушысы:
N = mg cos b (2)
Домалау үйкеліс күші шардың жылдамдығына тӘуелді болмайды деп есептейміз ( Fүйк =const). Бұл жағдайда маятник амплитудасының кемуі арифметикалық прогрессия заңы бойынша өтеді.
Маятник n тербеліс жасап, С орнынан С1 орнына ауысқанда (3-сурет) оның энергиясының азаюы:
DЕ = mgDh
мұндағы Dh – шардың ауырлық центрінің биіктігінің өзгерісі.
Бұл энергия үйкеліс күштерінің маятниктің жүріп өткен жолдарында істеген жұмысына тең болады:
DЕ =DА + DА1 (3)
мұндағы DА=Fүйк S – домалау үйкеліс күшінің жұмысы, DА1-ортаның үйкеліс күшінің жұмысы, ол аз болғандықтан, оны ескермеуге болады.
Сондықтан:
mgDh = Fүйк S (4)
3-суреттен көрініп тұрғандай Dћ жӘне Dl шамалары арасындағы байланыс мына қатынаспен анықталады:
Dћ =Dlsin b (5)
(5), (1), (2) қатынастарды (4) теңдеуге апарып қойсақ:
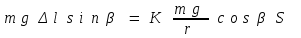(6) 3- сурет
Маятниктің жүрген S жолын былайша есептейміз.
Бастапқы уақыт кезіндегі ауытқу бұрышы - j
0, n тербелістен кейінгі ауытқу бұрышы - jn, маятниктің ұзындығы – L болса (3-сурет), онда маятник шарының (ауырлық центрінің ) n тербеліс жасағанда, жүрген жолы :
S=4nLjор (7)
S – маятник сызып өткен барлық доғалардың ұзындықтарының қосындысы. Доғаның ұзындығы оның радиусымен, олардың арасындағы бұрыштың көбейтіндісіне тең болады. Толық бір тербеліс кезінде маятник ұзындығы арифметикалық прогрессия бойынша кемитін, 4 рет доға сызып өтеді, сондықтан оның орташа мӘні:
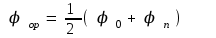(8)(8), (7) ескеріп, (6) теңдеуден домалау үйкеліс коэффициентін анықтауға болады:
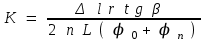(9)3-суреттен көрінетіндей:
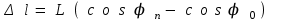
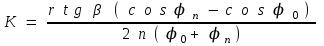(10)Тәжірибеде ауытқу бұрыштарының мәні аз болғандықтан, үйкеліс коэффициентін есептеу үшін мына жуық формуланы қолданады:
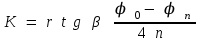(11)Көлбеу бет прибордың негізімен мықтап бекітілген. Онда маятниктің тербеліс санын есептейтін фотоэлектрондық өлшеуіш бар. Беттің көлбеулік бұрышын жайлап өзгертуге болады. Маятниктің тепе-теңдік жағдайдан ауытқуы дәлдігі 30/ болатын шкала бойынша өлшенеді. Приборда бетімен шар домалайтын пластинаны оңай ауыстыруға болады. Өлшеу FPM қондырғысында жасалады.