Файл: Методические указания к выполнению контрольной работы для студентов заочной формы обучения.docx

Продолжение табл. 2

1	2	3	4	5	6	7	8
12	6	55	4,5	62	31	80	2,5
13	7	56	1,4	63	32	81	1,5
14	7	56	2,5	64	32	81	2,3
15	8	57	1,5	65	33	82	1,2
16	8	57	2,3	66	33	82	3,4
17	9	58	1,2	67	34	83	1,3
18	9	58	3,4	68	34	83	4,5
19	10	59	1,3	69	35	84	1,4
20	10	59	4,5	70	35	84	2,5
21	11	60	1,4	71	36	85	1,5
22	11	60	2,5	72	36	85	2,3
23	12	61	1,5	73	37	86	1,2
24	12	61	2,3	74	37	86	3,4
25	13	62	1,2	75	38	87	1,3
26	13	62	3,4	76	38	87	4,5
27	14	63	1,3	77	39	88	1,4
28	14	63	4,5	78	39	88	2,5
29	15	64	1,4	79	40	89	1,5
30	15	64	2,5	80	40	89	2,3
31	16	65	1,5	81	41	90	1,2
32	16	65	2,3	82	41	90	3,4
33	17	66	1,2	83	42	91	1,3
34	17	66	3,4	84	42	91	4,5
35	18	67	1,3	85	43	92	1,4
36	18	67	4,5	86	43	92	2,5
37	19	68	1,4	87	44	93	1,5
38	19	68	2,5	88	44	93	2,3
39	20	69	1,5	89	45	94	1,2
40	20	69	2,3	90	45	94	3,4
41	21	70	1,2	91	46	95	1,3
42	21	70	3,4	92	46	95	4,5
43	22	71	1,3	93	47	96	1,4
44	22	71	4,5	94	47	96	2,5
45	23	72	1,4	95	48	97	1,5
46	23	72	2,5	96	48	97	2,3
47	24	73	1,5	97	49	98	1,2
48	24	73	2,3	98	49	98	3,4

---

Окончание табл. 2

1	2	3	4	5	6	7	8
49	25	74	1,2	99	50	99	1,3
50	25	74	3,4	0	50	99	4,5

МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, который в свою очередь включает 2 круга вопросов: отбор факторов и выбор уравнения регрессии.

Отбор факторов обычно осуществляется в два этапа:

1) теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;

2) количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции):

r_y,yr_y,x1r_yx2 .... r_y,xm

r_x1,yr_x1,x2r_x2x2 .... r_x2,xm

......

r_xm,yr_xm,x1r_xm,x2 .... r_xm,xm

где r_y,xj– линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками yи хj j=1;m, m -число факторов.

r_xj,xk– линейный парный коэффициент корреляции, измеряющий тесноту связи между признаками хjи хk j,k=1;m.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).

---

2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).

3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность - тесная линейная связь между факторами.

Мультиколлинеарность может привести к нежелательным последствиям:

1) оценки параметров становятся ненадежными. Они обнаруживают большие стандартные ошибки. С изменением объема наблюдений оценки меняются (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

2) затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

3) становится невозможным определить изолированное влияние факторов на результативный показатель.

---

Мультиколлинеарность имеет место, если определитель матрицы межфакторной корреляции близок к нулю:

.

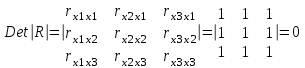Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет.Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них – исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, теоретический коэффициент детерминации -R²_y(x1...xm) снизится несущественно).
Определение факторов, ответственных за мультиколлинеарность, может быть основано на анализе матрицы межфакторной корреляции. При этом определяют пару признаков-факторов, которые сильнее всего связаны между собой (коэффициент линейной парной корреляции максимален по модулю). Из этой пары в наибольшей степени ответственным за мультиколлинеарность будет тот признак, который теснее связан с другими факторами модели (имеет более высокие по модулю значения коэффициентов парной линейной корреляции).
Еще один способ определения факторов, ответственных за мультиколлинеарность основан на вычислении коэффициентов множественной детерминации (R²_{xj(x1,...,xj-1,xj+1,...,xm)}), показывающего зависимость фактора xj от других факторов модели x1,...,xj-1, xj+1,...,xm. Чем ближе значение коэффициента множественной детерминации к единице, тем больше ответственность за мультиколлинеарность фактора, выступающего в роли зависимой переменной. Сравнивая между собой коэффициенты множественной детерминации для различных факторов можно проранжировать переменные по степени ответственности за мультиколлинеарность.

При выборе формы уравнения множественной регрессии предпочтение отдается линейной функции:

y_i=a+b₁·x1_i+ b₂·x2_i+...+ b_m·xm_i+u_i

в виду четкой интерпретации параметров.

Данное уравнение регрессии называют уравнением регрессии в естественном (натуральном) масштабе. Коэффициент регрессии

---

b_jпри факторе хjназывают условно-чистым коэффициентом регрессии. Он измеряет среднее по совокупности отклонение признака-результата от его средней величины при отклонении признака-фактора хj на единицу, при условии, что все прочие факторы модели не изменяются (зафиксированы на своих среднихуровнях).

Если не делать предположения о значениях прочих факторов, входящих в модель, то это означало бы, что каждый из них при изменении хj также изменялся бы (так как факторы связаны между собой), и своими изменениями оказывали бы влияние на признак-результат.

Расчет параметров уравнения линейной множественной регрессии

Параметры уравнения множественной регрессии можно оценить методом наименьших квадратов, составив и решив систему нормальных линейных уравнений.

Кроме того, для линейной множественной регрессии существует другой способ реализации МНК при оценке параметров - через -коэффициенты (через параметры уравнения регрессии в стандартных масштабах).

Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:

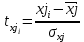, j=1;m,

где хj_i- значение переменной хj_i в i-ом наблюдении.

_.

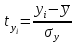Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение . Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:

.

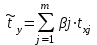Для оценки -коэффциентов применим МНК. При этом система нормальных уравнений будет иметь вид:

r_x1y=1+r_x1x2∙2+…+ r_x1xm∙m

r_x2y= r_x2x1∙1+2+…+ r_x2xm∙m

…

r_xmy=

---