Файл: Методические указания к выполнению контрольной работы для студентов заочной формы обучения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.01.2024
Просмотров: 148
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
rxmx1∙1+rxmx2∙2+…+m
Найденные из данной системы –коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:
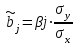, j=1;m; 
.
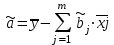Показатели тесноты связи факторов с результатом.
Если факторные признаки различны по своей сущности и (или) имеют различные единицы измерения, то коэффициенты регрессии bj при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям тесноты связи относят: частные коэффициенты эластичности, –коэффициенты, частные коэффициенты корреляции.
Частные коэффициенты эластичности Эj рассчитываются по формуле: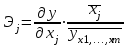
. Частный коэффициент эластичности показывают, на сколько процентов в среднем изменяется признак-результат y с изменением признака-фактора хj на один процент от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости Эj рассчитываются по формуле: 
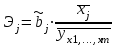, где 
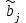– оценка коэффициента регрессии при j–ом факторе.
Стандартизированные частные коэффициенты регрессии - -коэффициенты (j) показывают, на какую часть своего среднего квадратического отклонения у изменится признак-результат y с изменением соответствующего фактора хj на величину своего среднего квадратического отклонения (хj) при неизменном влиянии прочих факторов (входящих в уравнение).
По коэффициентам эластичности и -коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент j может также интерпретироваться как показатель прямого (непосредственного) влияния j-ого фактора (xj) на результат (y). Во множественной регрессии
j-ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели). Косвенное влияние измеряется величиной: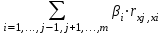
, где m- число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата – rxj,y.
Коэффициент частной корреляции измеряет «чистое» влияние фактора на результат при устранении воздействия прочих факторов модели.
Для расчета частных коэффициентов корреляции могут быть использованы парные коэффициенты корреляции.
Для случая зависимости y от двух факторов можно вычислить 2 коэффициента частной корреляции:
,
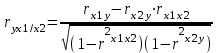(фактор х2 фиксирован).
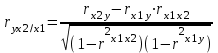
(фактор х1 фиксирован).
Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых устраняется).
Частные коэффициенты корреляции, рассчитанные по таким формулам изменяются от –1 до +1. Они используются не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях ryxm/x1,x2…xm-1 нет смысла вводить в уравнение m-ый фактор, т.к. его чистое влияние на результат несущественно.
Коэффициенты множественной детерминации и корреляции характеризуют совместное влияние всех факторов на результат.
По аналогии с парной регрессией можно определить долю вариации результата, объясненной вариацией включенных в модель факторов (2), в его общей вариации (2y). Ее количественная характеристика – теоретический множественный коэффициент детерминации (R2y(x1,...,xm)). Для линейного уравнения регрессии данный показатель может быть рассчитан через -коэффициенты, как:
.
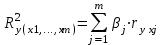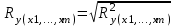- коэффициент множественной корреляции. Он принимает значения от 0 до 1 (в отличии от парного коэффициента корреляции, который может принимать отрицательные значения). Поэтому
R не может быть использован для интерпретации направления связи. Чем плотнее фактические значения yiрасполагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина Ry(x1,...,xm). Таким образом, при значении Rблизкомк 1, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат. При значении Rблизком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.
Оценка значимости полученного уравнения множественной регрессии.
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности: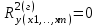
или b1=b2=…=bm=0 (гипотеза о незначимости уравнения регрессии, рассчитанного по данным генеральной совокупности).
Для ее проверки используют F-критерий Фишера.
При этом вычисляют фактическое (наблюдаемое) значение F-критерия, через коэффициент детерминации R2y(x1,...,xm), рассчитанный по данным конкретного наблюдения:
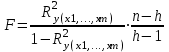, где n-число наблюдений; h – число оцениваемых параметров (в случае двухфакторной линейной регрессии h=3).
По таблицам распределения Фишера-Снедоккора находят критическое значение F-критерия (Fкр). Для этого задаются уровнем значимости (обычно его берут равным 0,05) и двумя числами степеней свободы k1=h-1 и k2=n-h.
Сравнивают фактическое значение F-критерия (Fнабл) с табличным Fкр(;k1;k2). Если Fнабл<Fкр(;k1;k2), то гипотезу о незначимости уравнения регрессии не отвергают. Если Fнабл>Fкр(;k1;k2), то выдвинутую гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии.
Задание № 2
На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения (уравнения). Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.
В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:
yt– текущая эндогенная переменная,
yt-1 – лаговая эндогенная переменная (отстоящая от текущей на 1 период назад),
yt-2 – тоже лаговая эндогенная переменная (отстоящая от текущей на 2 периода).
Все эконометрические модели предназначены для объяснения текущих значений эндогенных переменных по значениям предопределенных переменных.
В дальнейшем для простоты будем рассматривать в качестве предопределенных переменных только текущие экзогенные переменные (х).
Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.
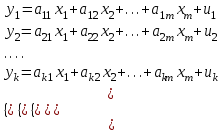
Найденные из данной системы –коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:
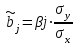, j=1;m; 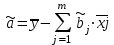.Показатели тесноты связи факторов с результатом.
Если факторные признаки различны по своей сущности и (или) имеют различные единицы измерения, то коэффициенты регрессии bj при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям тесноты связи относят: частные коэффициенты эластичности, –коэффициенты, частные коэффициенты корреляции.
Частные коэффициенты эластичности Эj рассчитываются по формуле:
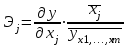. Частный коэффициент эластичности показывают, на сколько процентов в среднем изменяется признак-результат y с изменением признака-фактора хj на один процент от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости Эj рассчитываются по формул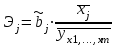е: , где 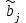– оценка коэффициента регрессии при j–ом факторе. Стандартизированные частные коэффициенты регрессии - -коэффициенты (j) показывают, на какую часть своего среднего квадратического отклонения у изменится признак-результат y с изменением соответствующего фактора хj на величину своего среднего квадратического отклонения (хj) при неизменном влиянии прочих факторов (входящих в уравнение).
По коэффициентам эластичности и -коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент j может также интерпретироваться как показатель прямого (непосредственного) влияния j-ого фактора (xj) на результат (y). Во множественной регрессии
j-ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели). Косвенное влияние измеряется величиной:
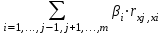, где m- число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата – rxj,y.Коэффициент частной корреляции измеряет «чистое» влияние фактора на результат при устранении воздействия прочих факторов модели.
Для расчета частных коэффициентов корреляции могут быть использованы парные коэффициенты корреляции.
Для случая зависимости y от двух факторов можно вычислить 2 коэффициента частной корреляции:
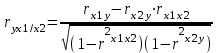,(фактор х2 фиксирован).
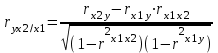
(фактор х1 фиксирован).
Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых устраняется).
Частные коэффициенты корреляции, рассчитанные по таким формулам изменяются от –1 до +1. Они используются не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях ryxm/x1,x2…xm-1 нет смысла вводить в уравнение m-ый фактор, т.к. его чистое влияние на результат несущественно.
Коэффициенты множественной детерминации и корреляции характеризуют совместное влияние всех факторов на результат.
По аналогии с парной регрессией можно определить долю вариации результата, объясненной вариацией включенных в модель факторов (2), в его общей вариации (2y). Ее количественная характеристика – теоретический множественный коэффициент детерминации (R2y(x1,...,xm)). Для линейного уравнения регрессии данный показатель может быть рассчитан через -коэффициенты, как:
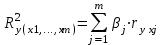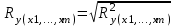. - коэффициент множественной корреляции. Он принимает значения от 0 до 1 (в отличии от парного коэффициента корреляции, который может принимать отрицательные значения). Поэтому
R не может быть использован для интерпретации направления связи. Чем плотнее фактические значения yiрасполагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина Ry(x1,...,xm). Таким образом, при значении Rблизкомк 1, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат. При значении Rблизком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.
Оценка значимости полученного уравнения множественной регрессии.
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности:
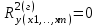или b1=b2=…=bm=0 (гипотеза о незначимости уравнения регрессии, рассчитанного по данным генеральной совокупности).Для ее проверки используют F-критерий Фишера.
При этом вычисляют фактическое (наблюдаемое) значение F-критерия, через коэффициент детерминации R2y(x1,...,xm), рассчитанный по данным конкретного наблюдения:
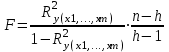, где n-число наблюдений; h – число оцениваемых параметров (в случае двухфакторной линейной регрессии h=3).По таблицам распределения Фишера-Снедоккора находят критическое значение F-критерия (Fкр). Для этого задаются уровнем значимости (обычно его берут равным 0,05) и двумя числами степеней свободы k1=h-1 и k2=n-h.
Сравнивают фактическое значение F-критерия (Fнабл) с табличным Fкр(;k1;k2). Если Fнабл<Fкр(;k1;k2), то гипотезу о незначимости уравнения регрессии не отвергают. Если Fнабл>Fкр(;k1;k2), то выдвинутую гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии.
Задание № 2
На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
-
Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения. -
Рассчитать частные коэффициенты эластичности. Сделать вывод. -
Определить стандартизованные коэффициенты регрессии (-коэффициенты). Сделать вывод. -
Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы. -
Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
CИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения (уравнения). Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.
В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:
-
Экзогенные (независимые) – значения которых задаются «извне», автономно, в определенной степени они являются управляемыми (планируемыми) (X); -
Эндогенные (зависимые) - значения которых определяются внутри модели, или взаимозависимые (Y). -
Лаговые – экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например:
yt– текущая эндогенная переменная,
yt-1 – лаговая эндогенная переменная (отстоящая от текущей на 1 период назад),
yt-2 – тоже лаговая эндогенная переменная (отстоящая от текущей на 2 периода).
-
Предопределенные переменные – переменные, определяемые вне модели. К ним относятся лаговые и текущие экзогенные переменные (xt, xt-1), а также лаговые эндогенные переменные (yt-1).
Все эконометрические модели предназначены для объяснения текущих значений эндогенных переменных по значениям предопределенных переменных.
В дальнейшем для простоты будем рассматривать в качестве предопределенных переменных только текущие экзогенные переменные (х).
Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.
-
Система независимых уравнений, когда каждая зависимая переменная (y) рассматривается как функция только от предопределенных переменных (х):
-
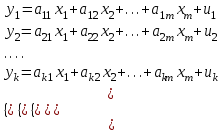
Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений: