Файл: ВсяМехЛАБраб2части.doc

Скорость шарика можно определить, зная расстояние между метками на сосуде и времяt, за которое шарик проходит это расстояние: .

Подставив эти равенства в (6), выразим из него коэффициент вязкости:

(7) - эта формула справедлива для шарика, падающего в безгранично простирающейся жидкости. В данном случае необходимо ввести поправочный множитель , учитывающий влияние стенок и дна цилиндра на падение шарика.

Получаем окончательно рабочую расчетную формулу для экспериментального определения коэффициента вязкости жидкости методом Стокса:

(8)

Вопросы к допуску.

1. Какие силы действуют на падающий в жидкости шарик? Каковы характер и динамика его движения?

2. Записать формулу закона Стокса и пояснить входящие в нее обозначения?

3. Каковы условия применимости закона Стокса? Как они учтены в работе?

4. Записать расчетную формулу для вязкости жидкости? Пояснить каким образом находятся значения входящих в нее величин в данной работе.

5. Чем обусловлено положение верхней метки на цилиндрическом сосуде по отношению к краю жидкости в нем?

6. Пояснить характер зависимости скорости шарика [формула (5)] по рис.2.

7. От чего зависит получаемое значение вязкости? Каковы источники возможных погрешностей результата?

Содержание экспериментальных заданий.

Задание 1. Вычисление расстояния релаксации.

1. Выбрать шарик наибольшего радиуса и измерить его диаметр, массу, вычислить объем и среднюю плотность.

2. Измерить линейкой расстояние d от поверхности масла в цилиндрическом сосуде до верхней отметки.

3. По справочной таблице найти значение плотности и коэффициента вязкости касторового масла, записать в тетрадь.

4. По формуле (6) рассчитать скорость 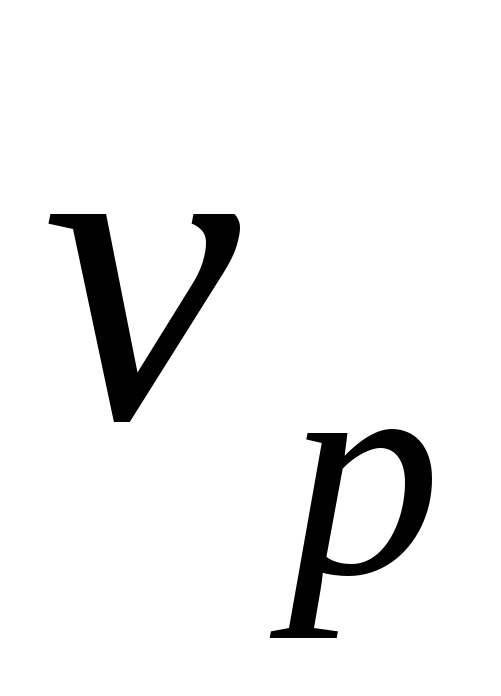равномерного падения шарика.

5. На основе формулы (5) найти минимальное время 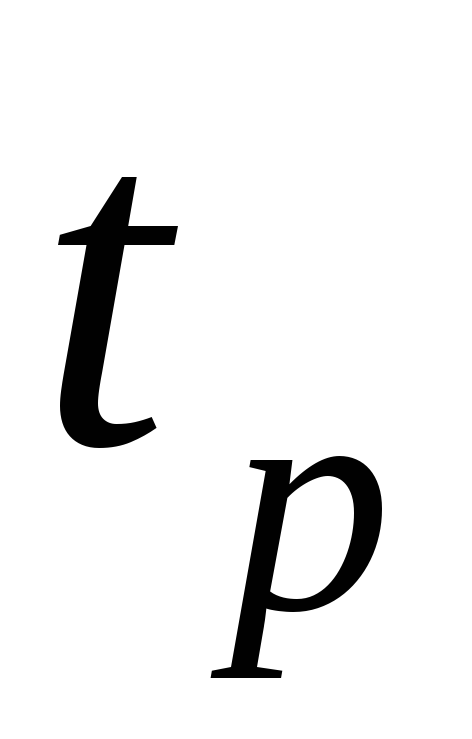, соответствующее значению скорости, найденному в предыдущем пункте.

6. Интегрированием формулы (5) в пределах от t=0 до t=t_р вычислить путь S, проходимый шариком при его неравномерном движении в жидкости.

7. Сравнить полученное значение S с расстоянием d от поверхности жидкости в сосуде до верхней метки. Сделать соответствующий вывод о применимости расчетной формулы.

Задание 2. Экспериментальное определение вязкости касторового масла.

1. Взять 3 металлических шарика (стальные или свинцовые) и микрометром произвести несколько измерений их диаметров. Вычислить средние значения радиусов данных шариков. Занести эти и последующие результаты в таблицу.

2. Свободно отпустить шарик в исследуемую жидкость и засечь время 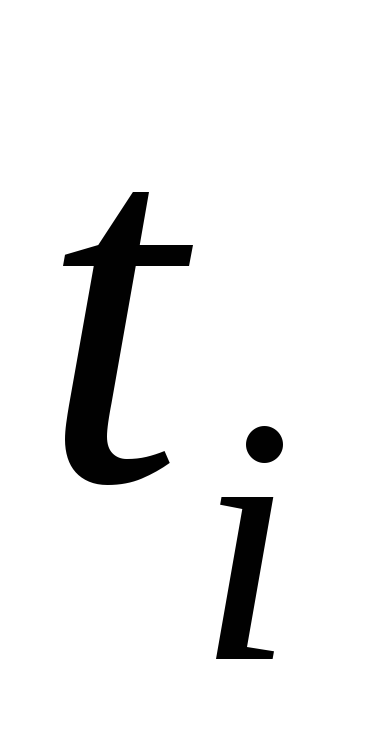прохождения им расстояния между метками. Проделать это для каждого из взятых шариков,i =1, 2, 3.

3. Измерить расстояние между метками и записать какова абсолютная погрешность этого значения.

4. Определить температуру исследуемой жидкости (температуру воздуха в помещении).

5. Для каждого опыта вычислить по расчетной формуле полученное значение вязкости. Найти его среднее значение и сравнить с табличным.

6. Сделать вывод о правильности проведенного эксперимента и пояснить возможные причины расхождения теоретического и экспериментального значений коэффициента вязкости касторового масла.

7. Оценить погрешность результат проделанного измерения как косвенного многократного измерения. Записать ответ в форме 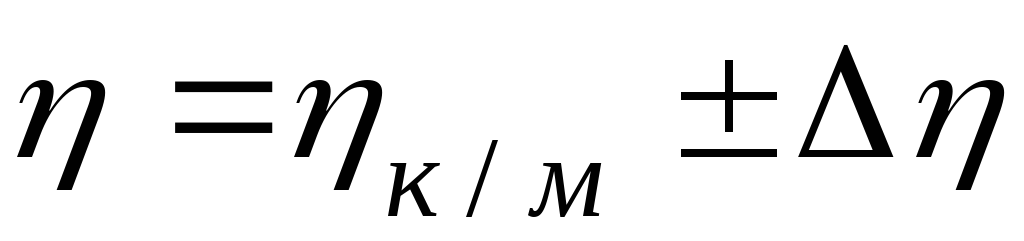,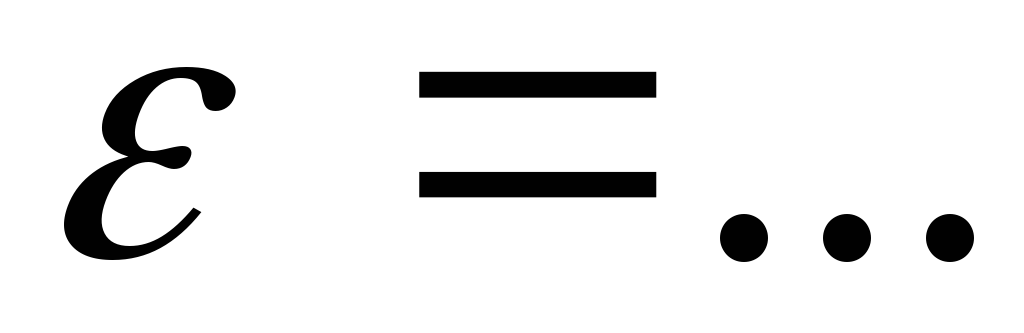(степень доверия Р=...).

Задание 3. Исследование зависимости скорости падения шарика в вязкой жидкости.

1. Подставьте полученные в ходе выполнения эксперимента числовые значения соответствующих величин в формулу (5) и запишите ее вид после проведения соответствующих вычислений (возьмите данные, соответствующие падению одного из шариков).

2. Постройте на миллиметровой бумаге график зависимости скорости падения шарика от времени падения с указанием выбранных масштабов. Точный график можно построить в системе Mathcad на компьютере.

3. Сравните значение скорости равномерного движения шарика, полученное из графика с тем, что было посчитано в ходе опыта.

4. По графику определить время 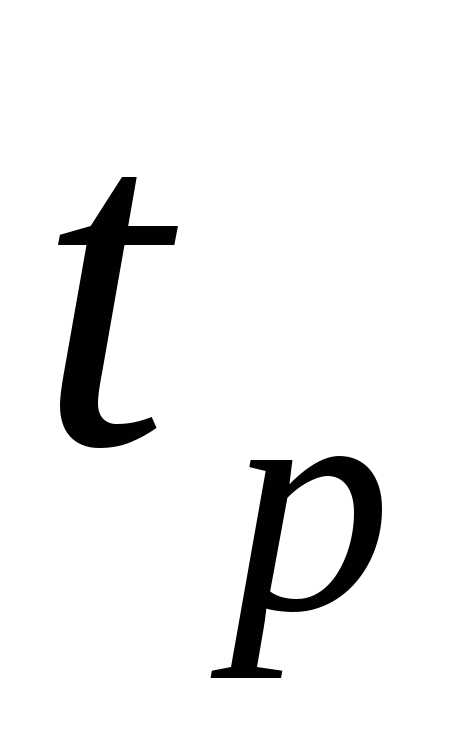, через которое скорость шарика перестанет меняться. Посчитать площадь фигуры под графиком на участке от начала движения до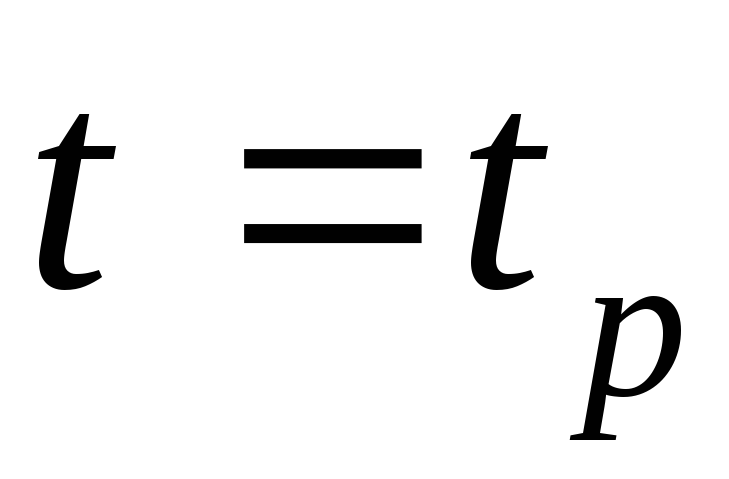. Сравнить эту величину с расстояниемd от поверхности жидкости в сосуде по верхней метки.

5. Сделайте необходимый вывод.

Вопросы к отчету:

1. Поясните сущность явления вязкого трения. Какова природа сил внутреннего трения жидкости?

2. Сформулируйте закон Ньютона и поясните входящие в него величины.

3. Что такое коэффициент вязкости?

4. Запишите формулу Стокса и укажите условия ее применимости. Докажите справедливость формулы (3) методом размерностей.

5. Какое движение жидкости называют ламинарным? Запишите условие ламинарности.

6. Выведите формулу зависимости скорости падения шарика от времени из динамического уравнения его движения в вязкой жидкости.

7. Сформулируйте утверждения, отражающие основные результаты данного эксперимента.

8. Перечислить основные источники погрешностей измерений, проводимых в данной работе. Как они были вами учтены при оценке точности результата?

Лабораторная работа № 1.4.

Определение модуля Юнга металлической проволоки.

Цель работы: познакомиться с числовыми характеристиками и законами упругой продольной деформации твердых тел; исследовать упругие свойства металла, в частности на практике изучить деформацию растяжения на примере металлической проволоки; познакомиться с методом экспериментального нахождения модуля Юнга.

Приборы и принадлежности: нихромовая или стальная проволока, закрепленная с одного конца, грузы и подвесная опора для них, два микроскопа с окулярными шкалами, микрометр, масштабная линейка.

Краткая теория вопроса и метода измерения.

Напомним, что механика твердого тела основана на использовании абстрактной модели – понятии «абсолютно твердого тела». Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться, т.е. при любых условиях расстояние между какими-либо двумя его точками (или частицами тела) остается постоянным. В природе абсолютно твердых тел нет, т.е. это – идеализированная модель.

Деформацией твердого тела (объекта природы) называется изменение его размеров и объема, сопровождающееся чаще всего изменением формы этого тела. Лишь в случаях всестороннего равномерно распределенного по поверхности тела сжатия или растяжения форма тела не меняется.

Причины деформаций:

- изменение температуры (тепловое расширение);

- внешние силовые воздействия.

При деформациях происходят смещения частиц, находящихся в узлах кристаллической решетки, из первоначальных положений в новые, т.е. изменяется взаимное расположение частиц тела. Это приводит к следующему:

1. возникновению упругих сил взаимодействия между частицами (смещенными от положения равновесия), которые стремятся вернуть их в исходные положения; внутренние упругие силы уравновешивают внешние силовые факторы, приложенные к телу;

2. увеличению потенциальной энергии деформируемого тела на величину работы, совершенной при смещении частиц, по преодолению внутренних упругих сил.

Различают упругие и пластические (остаточные) деформации. В первом случае тело полностью, а во втором лишь частично, восстанавливает свои прежние размеры и форму после снятия внешней нагрузки. В реальности все деформации в той или иной степени пластичны. Но если остаточные деформации пренебрежимо малы, то можно считать деформацию упругой. Этому отвечают малые деформации. В пределах малых деформаций все деформации удовлетворяют следующим основным законам:

- в пределах упругости деформация пропорциональна величине внешнего усилия;

- перемена знака внешнего усилия вызывает только перемену знака деформации, без изменения ее абсолютной величины;

- при действии нескольких внешних усилий общая деформация равна сумме частных деформаций.

В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения (сжатия) и сдвига.

Остановимся на одностороннем или продольном растяжении (сжатии), которое состоит в увеличении (уменьшении) длины тела под действием растягивающей (сжимающей) силы F. Для этого рассмотрим однородный стержень (проволоку) длиной l и площадью поперечного сечения S, один конец которого закреплен, а к другому приложена сила F, изменившая длину стержня на величину . Величина силы, приходящаяся на единицу площади поперечного сечения стержня, называется напряжением:(1).

Мерой деформации служит относительная деформация, которая в данном случае определяется так:

(2) - относительная продольная деформация.

Величины (1) и (2) связаны в случае упругих деформаций по закону Гука:

(3) или (3’) (4).

Коэффициент пропорциональности Е в формуле (3) называется модулем Юнга – характеристика упругих свойств материала, а коэффициент k в (4) – коэффициентом упругости тела. Из (3) следует, что модуль Юнга определяется напряжением, вызывающим удвоение длины стержня. Т.е. модуль Юнга равен напряжению, при котором относительное удлинение стало бы равным единице. Если бы при таком относительном удлинении еще сохранялась пропорциональность между ним и напряжением. В действительности, гораздо раньше, чем будет достигнуто напряжение, равное модулю Юнга, тело начнет испытывать пластическую деформацию, а затем подвергнется разрыву.

Деформация твердых тел подчиняется закону Гука лишь до определенного предела, называемого пределом пропорциональности.

Продольная деформация стержня всегда вызывает его поперечную деформацию: удлиняясь стержень становится соответственно тоньше. относительная поперечная деформация: (5), где- диаметр стержня.