Файл: ВсяМехЛАБраб2части.doc

Из опыта вытекает взаимосвязь: (6), где- положительный коэффициент, зависящий от свойств материала, называемыйкоэффициентом Пуассона.

Далее рассчитаем работу, которую нужно совершить, чтобы растянуть данный стержень на величину . Чтобы растягивать стержень нужно в каждый момент времени действовать на него с силой, соответствующей текущему удлинению и определяемой по формуле (4). Т.е.:. Принимая за ноль значение потенциальной энергии тела в отсутствие деформации, получим выражение для определения потенциальной энергии упруго деформируемого тела:или(7). ГдеV – объем стержня (изменение объема стержня при его деформации здесь не учитывалось!).

Величина (8) называетсяплотностью потенциальной энергии. В случае однородного стержня при одинаковой в любой его точке деформации энергию можно считать равномерно распределенной по объему стержня. В общем случае неоднородной деформации плотность энергии может меняться от точки к точке.

Для проведения измерений выразим модуль Юнга из формулы (3’):

.

В случае исследования проволоки круглого сечения имеем , тогдарасчетная формула для нахождения значения модуля Юнга материала проволоки примет окончательный вид: (9).

Экспериментальная установка схематично изображена на рисунке.

Микроскопы первоначально настраиваются на видение каждой из 2-х меток. Нагружение проволоки приводит к их смещению, а разность величин этих смещений дает величину абсолютной деформации соответствующего участка проволоки между метками.

Д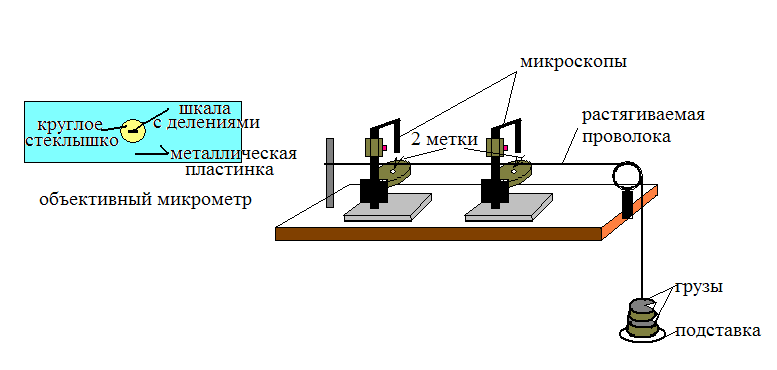ля измерения малых смещений меток используют микроскоп с встроенным окулярным микрометром. Окулярный микрометр представляет собой круглое стекло, на котором нанесены деления. Вся шкала обычно имеет длину 1 см и содержит 50 равных делений. Эта шкала помещается в окуляре между линзами в том месте, где получается изображение предмета. Цена деления окулярного микрометра определяется предварительно по объективному микрометру с ценой деления 0,01 мм.

Вопросы к допуску.

1. Какой вид деформации твердого тела будет исследоваться вами в данной работе?

2. Какие величины количественно характеризуют этот вид деформации?

3. Дайте определение и поясните физический смысл модуля Юнга? Эта величина служит характеристикой данного образца, материала из которого он изготовлен или того и другого сразу?

4. В чем существенное отличие модуля Юнга от коэффициента упругости? Могут ли эти величины быть численно равны? Запишите в тетрадь справочные данные о примерах значений величин E и k.

5. Имеет ли смысл говорить о значении модуля Юнга в случае неупругой деформации некоторого тела?

6. Дать определение продольной и поперечной относительных деформаций стержня. Как связаны эти величины?

7. Записать расчетную формулу и пояснить входящие в нее величины и способ их измерения в данной работе.

8. Как в работе определяется цена деления окулярной шкалы?

9. Пояснить величины, стоящие в заголовках столбцов таблицы 1. Имеет ли смысл нахождение среднего значения величины из последнего столбца этой таблицы? Почему? Чему на графике соответствует среднее значение указанной величины? Как оно связано с характером деформации?

10. Каковы возможные источники погрешностей искомого результата? Какие ваши действия по ходу работы могут их уменьшить?

11. Какие переменные в формуле (9) будут браться в качестве отдельных множителей при оценке погрешности косвенного измерения? Каково их количество?

Содержание экспериментальных заданий.

Задание 1. Определение цены деления шкалы окулярного микрометра

1. Поместить объективный микрометр в поле обзора микроскопа и получить его видимость в окуляре микроскопа.

2. Посчитать число делений объективного микрометра, умещающихся на n делениях шкалы окуляра. Найти количество делений микрометра, приходящихся на одно деление окуляра.

3. Зная цену деления объективного микрометра вычислить цену деления окулярной шкалы микроскопа. Записать полученное значение под таблицей 1.

Задание 2. Определение сечения S данной проволоки и длины исследуемого участка .

1. Провести 10 измерений микрометром диаметра проволоки в различных местах между установленными метками.

2. Вычислить среднее значение диаметра проволоки 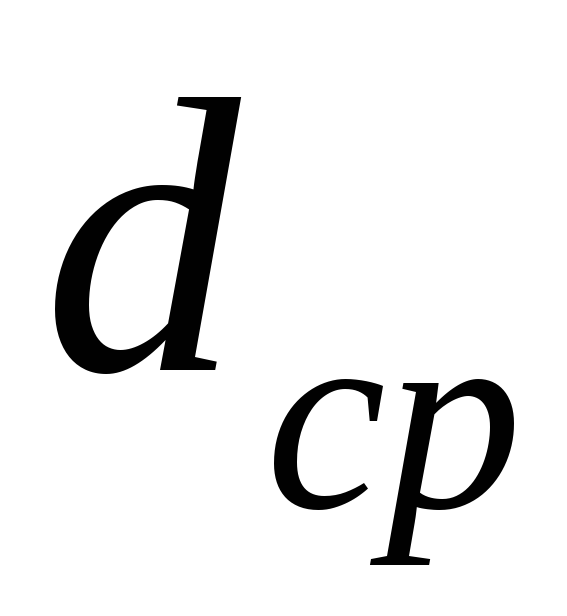и рассчитать погрешность проделанных многократных прямых измерений.

3. Произвести вычисление средней площади поперечного сечения данной проволоки .

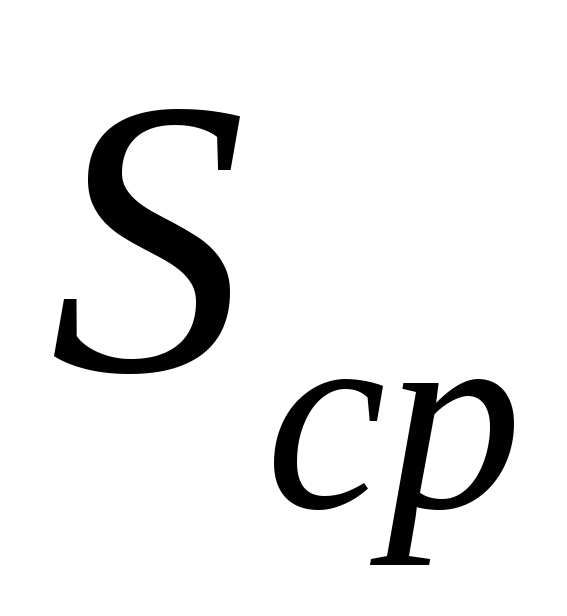4. С помощью миллиметровой линейки измерить расстояние 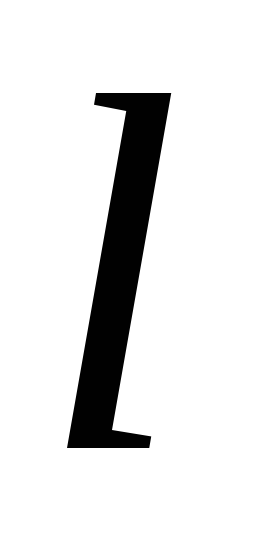между двумя метками при незначительном натяжении закрепленной проволоки. Это и будет служить исходным значением длины образца.

5. Вычислить коэффициент 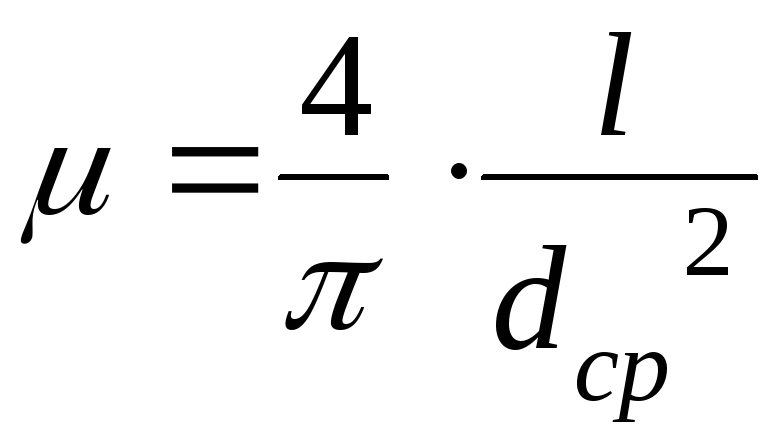(10)

6. Сохранить полученное исходное состояние проволоки для проведения действий из задания 3.

Задание 3. Построение графика растяжения проволоки.

1. Зафиксировать по окулярным шкалам положение меток в исходном состоянии проволоки (см. задание 2).

2. Осторожно нагрузить незакрепленный конец проволоки грузом известной массы .

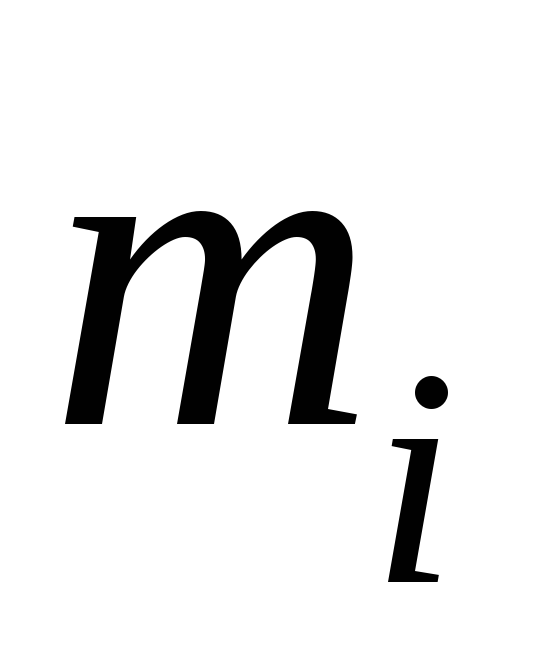3. Найти с помощью микроскопов соответствующие смещения 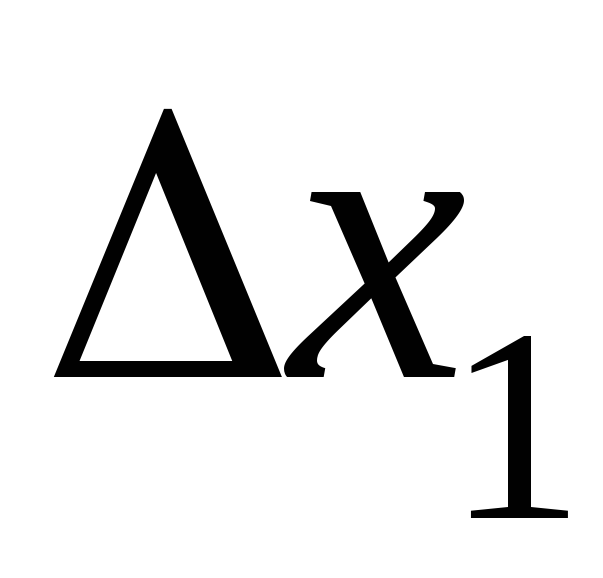и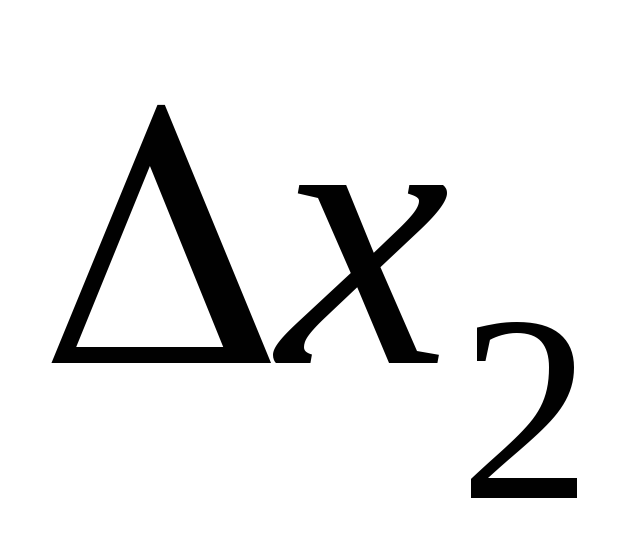каждой метки в делениях окулярной шкалы.

4. Вычислить соответствующее растяжение проволоки на данном участке 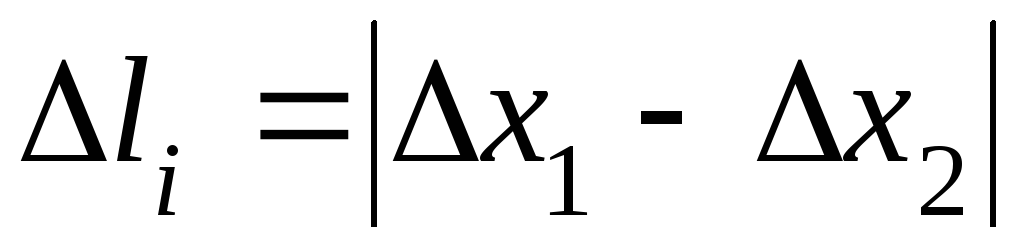и записать его значение в метрах, зная цену деления окулярной шкалы (см. задание 1).

5. Полученные в пунктах 1)-4) значения указанных величин занести в таблицу 1, проделав аналогичную последовательность для разных по массе нагрузках не менее 7 раз.

Таблица 1.

6. Построить на миллиметровой бумаге сглаженный график зависимости 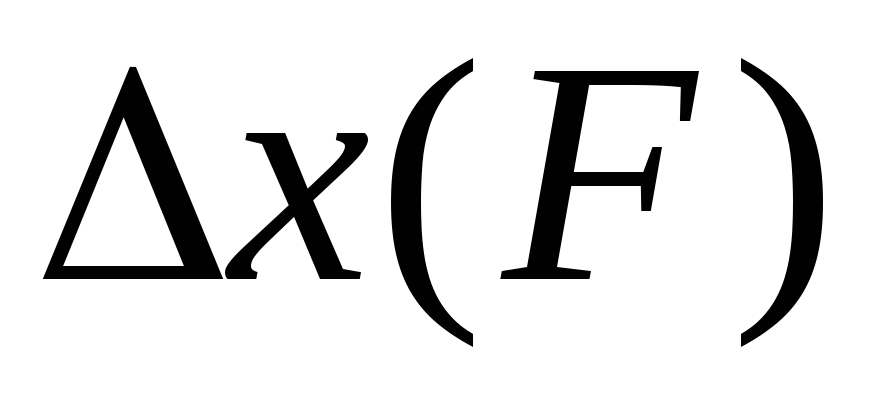, отложив по вертикали значения силы, а по горизонтали соответствующие удлинения.

7. Укажите отчетливо точки, соответствующие экспериментально полученным значениям из таблицы 1.

8. Проведите прямую, наиболее близко соответствующую положению отмеченных экспериментальных точек. Найдите угловой коэффициент наклона 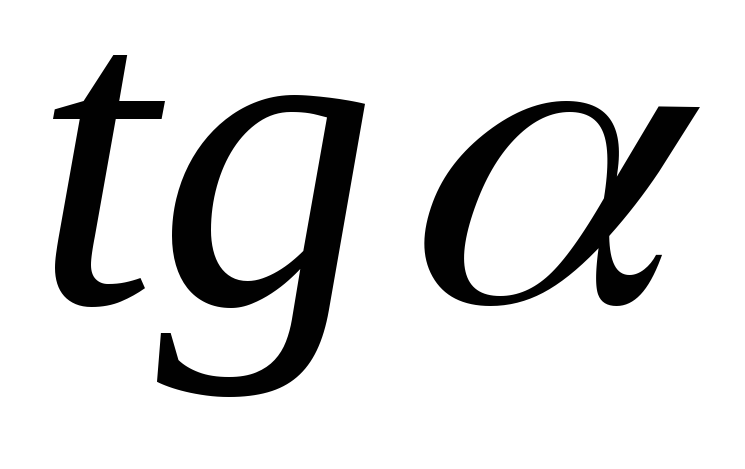этой прямой к горизонтальной оси.

9. На основе анализа полученной формы графика сделать вывод о характере деформации проволоки и о возможности применить расчетную формулу.

10. Проделав нужные вычисления заполнить последний столбец таблицы 1.

11. Подумайте, как связана величина 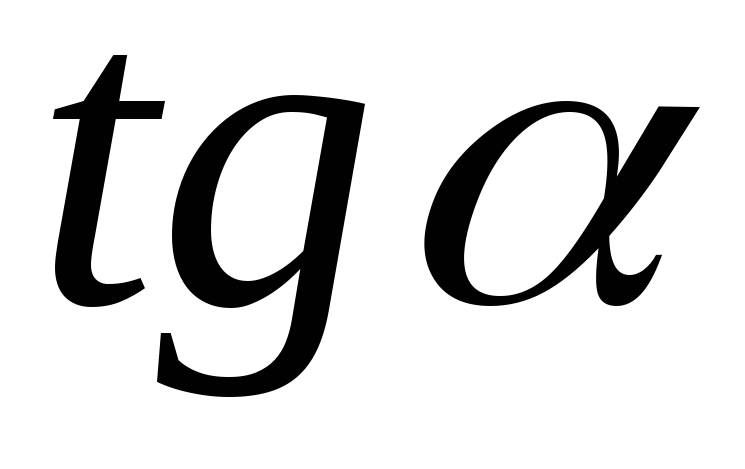с данными последнего столбца таблицы 1?

Задание 4. Определение значения модуля Юнга материала проволоки.

1. Вычислить по данным эксперимента значение Е на основе расчетной формулы (9), взяв среднее значение 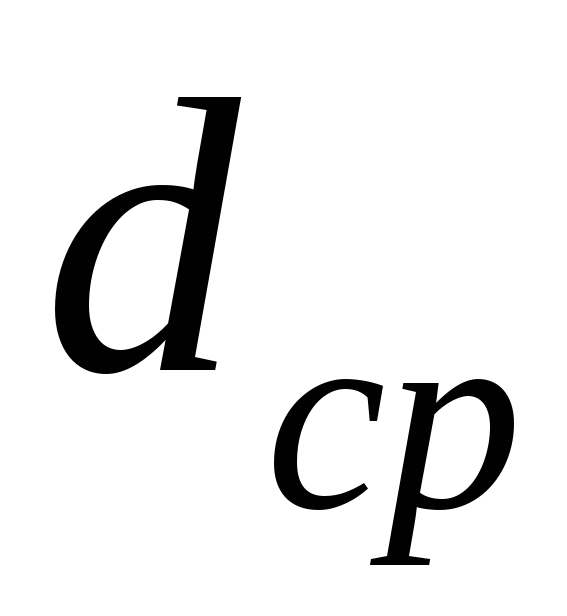диаметра проволоки.

2. Сравните полученное значение с величиной 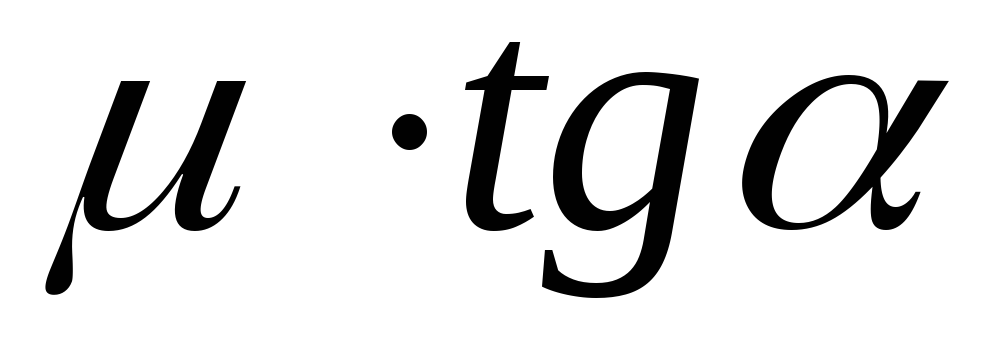. Поясните результат этого сравнения.

3. Оценить погрешность результата проделанного измерения как косвенного однократного измерения. Записать ответ в форме ,.

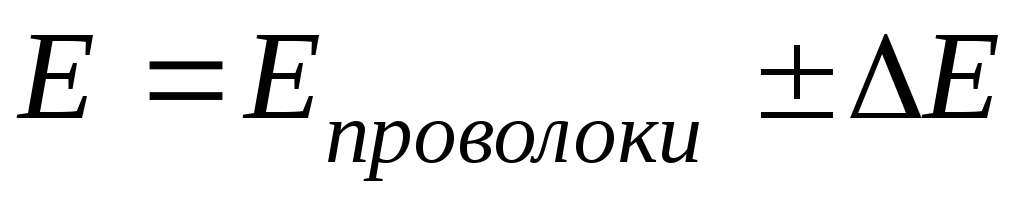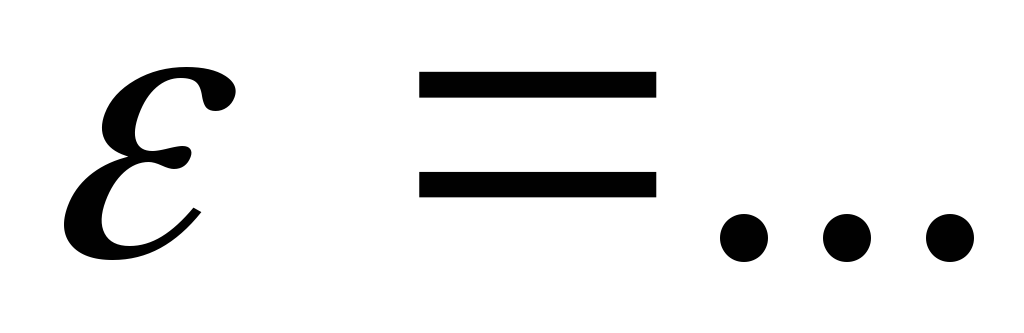4. Найдите в справочной таблице значение модуля Юнга, близкое к полученному вами значению Е. Какому материалу согласно справочной таблице оно соответствует?

5. Сделайте вывод о соответствии или несоответствии полученного результата материалу, из которого изготовлена исследуемая проволока.

Задание 5. Исследование зависимости плотности потенциальной энергии деформации от относительного удлинения.

1. Взяв значение величины Е. полученное в задании 4, и на основе данных из таблицы 1 заполните таблицу 2. При расчете используйте формулу (8). Таблица 2.

№ п/п		Е, Н/м2	, Дж/м3
1.
...
7-10

2. Постройте график зависимости .

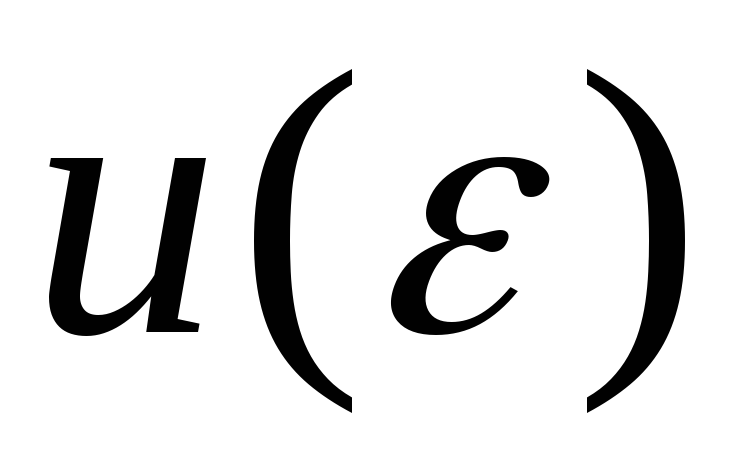3. Охарактеризуйте тип зависимости на основе полученного графика и сделайте пояснения на основе рассмотрения сути происходящих при деформации физических процессов.

Вопросы к отчету:

1. Как проявляются упругие свойства металлов?

2. Какая деформация называется продольной? Что служит ее мерой?

3. Изобразите диаграмму растяжения металлического стержня и укажите на ней точки соответствующие пределу пропорциональности и пределу упругости. В чем сходство и в чем различие этих двух понятий?

4. Что представляет собой величина d в формуле (5) в случае стержня с прямоугольным сечением?

5. Выведите расчетную формулу. Какие допущения были сделаны при этом?

6. Каковы единицы измерения модуля Юнга?

7. Что называется потенциальной энергией? Что принимают на потенциальную энергию упругой деформации?

8. Как экспериментально можно определить модуль Юнга некоторого металла?

9. Каким законам удовлетворяют малые деформации? Чему соответствует условие их «малости»? Как и где в ходе работы применялся закон сложения деформаций?