Файл: Faustova.docx

3.3.Методика изучения величин Длина

На первом этапе учитель выясняет, какие представления имеют учащиеся об изучаемой величине. С этой целью можно, например, показать два карандаша одного цвета, но разной длины и попросить учащихся охарактеризовать их. Умело направляя ответы детей с помощью наводящих вопросов, следует обратить их внима­ние именно на признак длины и добиться, чтобы они не только ответили, что один из карандашей длиннее, а другой короче, но и попытались доказать это, например, путем приложения каран­дашей друг к другу. Учитель варьирует подобные задания, исполь­зуя при этом различные предметы, модели, рисунки, стремясь добиться того, чтобы учащиеся осознали, что предметы обладают свойством иметь длину и что их, например карандаши, можно срав­нивать по этому признаку путем наложения, приложения и на глаз.

Использование мерок для сравнения длин отрезков подготав­ливает учащихся к осознанию самого процесса измерения. На­пример, на доске начерчены два отрезка (90 см и 120 см). При этом они расположены так, что дать обоснованный ответ о том, какой из отрезков длиннее (короче), нельзя. (Способ наложения или при­ложения в этом случае не применим.). Учитель показывает уче­никам планочку длиной 30 см, называет ее меркой и предлагает с ее помощью сравнить длины отрезков. Учащиеся самостоятельно укладывают планку сначала по длине одного отрезка, затем дру­гого. Получают результат: 3<4 — и делают соответствующий вы­вод: первый отрезок короче, а второй длиннее. Аналогичное зада­ние выполняют с другой планкой (15 см). Получают: 6<8 — и делают тот же вывод: первый отрезок короче второго. Затем учи­тель предлагает уложить первую планку по длине второго отрезка (она укладывается 4 раза), а вторую — по длине первого (укла­дывается 6 раз). Получается: 6>4. «Мы получили, что первый отрезок длиннее второго. Может быть, мы раньше делали непра­вильный вывод?» — спрашивает учитель.

Созданная проблемная ситуация поможет учащимся осознать тот факт, что для сравнения длин отрезков необходимо пользоваться одной меркой. Это подготовит их к пониманию того, что числовое значение величины зависит от единицы измерения. Ус­воение этого продолжается в процессе различных упражнений. Используя групповую форму работы на уроке, можно провести, на­пример, такую практическую работу. На каждой парте модель отрезка (синего цвета) и две мерки (одна красного, а другая зеленого цвета). Учитель дает задание: «Ученики, сидящие слева, измеряют отрезок красной меркой, а сидящие справа — зеленой». В процессе измерения получаются разные числовые значения величины. Это позволяет учителю задать проблемный вопрос: «Разве может быть так: измерялся один и тот же отрезок, а числа получились совсем разные? В чем дело? Была допущена ошибка?» (Учащиеся должны осознать, что причина разных ответов — в ис­пользовании разных мерок при измерении одного и того же от­резка.)

Можно предложить и такое задание: «Трое учеников измеряли один и тот же отрезок (отрезок предварительно вычерчивается в тетрадях). В результате первый из них получил в ответе 8, вто­рой — 4, а третий — 2. Почему так могло получиться и кто из них прав?» Дети должны ответить, что первый принял за единицу изме­рения длину одной клеточки, второй — длину двух клето­чек, а третий — длину четырех клеточек. Каждый из измерявших был бы прав, если бы указал в ответе единицу измерения. Учитель может сделать на доске такую условную запись: 8_□, 4_□□, 2 _□□□□. Аналогичным заданием является измерение длины класса шагами или длины доски разными мерками. В результате практических работ учащиеся подводятся к выводу о необходимости введения единицы измерения длины. В качестве первой единицы измерения длины вводится сантиметр.

М.1, ч.1, с.60

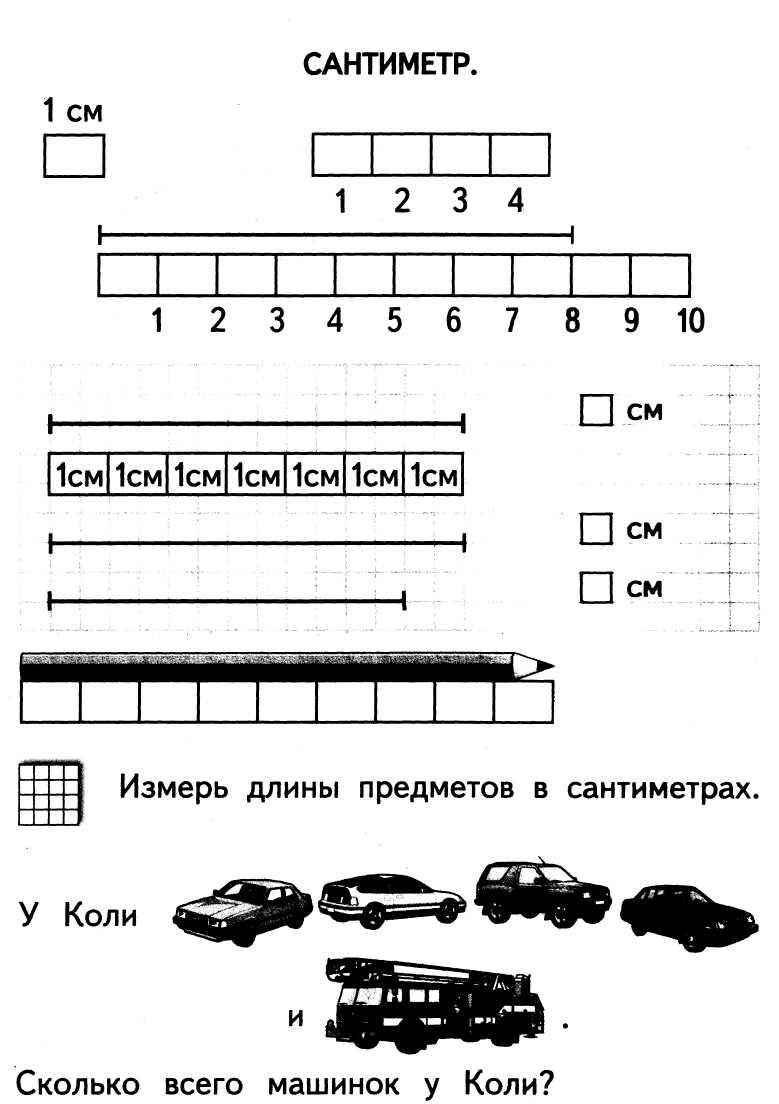
Прежде чем ознакомить детей с линейкой и с правилами измерения длин отрезков с помощью этого инструмента, учитель предлагает ученикам ряд заданий:

• измерение данного отрезка с помощью модели сантиметра путём укладывания на отрезке и подсчёта числа шагов;

• изготовление и измерение отрезка с помощью неоцифрованной линейки;

• нанесение шкалы на неоцифрованную линейку;

• измерение ею длин отрезков, ознакомление с правилами измерения.

Выполнение таких заданий позволяет предупредить главную ошибку при измерении отрезков: прикладывание к началу отрезка деления линейки с цифрой 1.

Учащиеся упражняются в сложении и вычитании длин, выра­женных в единицах одного наименования, в процессе решения за­дач на увеличение и уменьшение длины отрезка, на разностное сравнение, на нахождение суммы длин отрезков.

Введение новых единиц длины — дециметра и метра осущест­вляется в процессе практической деятельности; соотношения между единицами длины закрепляются путем упражнений.

Масса

В концентре «Десяток» учащиеся знакомятся с массой и еди­ницей ее измерения — килограммом.

При изучении этой темы необходимо особенно внимательно отнестись к терминологии. Дело в том, что до последнего времени при измерении массы с помощью чашечных весов было распрост­ранено неудачное использование слова «вес». Масса и вес не одно и то же. Вес представляет собой силу, т. е. произведение массы на ускорение. Поэтому вместо вопроса: «Сколько весит предмет?» — следует приучить детей к такой форме вопроса «Какова масса предмета?» Эта форма вопроса принята теперь и в учебниках математики, начиная с I класса.

В методике формирования представления о массе можно выделить этапы, о которых шла речь ранее.

Прежде всего, необходимо выяснить, какие представления имеются у детей о массе, и уточнить их. Для этого учитель может, например, создать такую ситуацию.

Поставить на стол два одинаковых по цвету и размеру кубика (их можно изготовить один из дерева, другой из картона). Ни­каких внешних признаков различия учащиеся не могут обнару­жить. Учитель подчеркивает, что различие между ними все-таки существует (учащиеся заинтересованы и пытаются угадать, в чем оно). У кого-то возникает желание рассмотреть кубики поближе, взять их в руки. Подняв кубики, они сразу же дают ответ: «Этот кубик тяжелее (легче)». Учитель уточняет, что со словами «легче» и «тяжелее» связано такое свойство предметов, как м а с с а . Вместо слов «предмет легче» или «предмет тяжелее» в математике принято говорить «масса предмета меньше» или «масса больше».

Рис. 1 Рис. 2

Затем учитель предлагает каждому из вызванных учеников взять в руки две книги (которые незначительно отличаются мас­сой) — одну в левую руку, а другую в правую — и определить, какая из книг тяжелее. Выслушав различные мнения, учитель под­черкивает, что, оказывается, не всегда можно сравнить массы предметов, просто взяв их в руки. В таких случаях нужно восполь­зоваться простейшим прибором — чашечными весами. Учитель показывает весы, изображает их схематически на доске (рис. 1) и разъясняет принцип их использования при сравнении масс предме­тов. Необходимые навыки закрепляются в процессе упражнений. Внимание учеников фиксируется на положении стрелок при пустых чашках весов, а затем после того, как на них положены предметы. Учитель сообщает, что, так же как и для измерения длины, для измерения массы необходима единица измерения. Такой единицей является килограмм. Учитель показывает гири в 1 кг, 2 кг, 5 кг. Учащиеся выполняют упражнения по взвешиванию предметов, в процессе чего они не только расширяют свои представления о ве­личинах, но и лучше усваивают другие вопросы курса математики, в частности совершенствуют свои вычислительные навыки. С этой целью предлагается такое задание: «Подумайте, какие предметы (какой массы) следует поставить на правую чашку весов (рис. 2), чтобы чашки весов были в равновесии». (На наборном полотне или на фланелеграфе размещены карточки, изображающие пред­меты различной массы: 2 кг, 3 кг, 5 кг, 1 кг и т. д.).

М.1, ч.2, с. 34

В процессе решения задач на нахождение суммы, остатка, на разностное сравнение и др. учащиеся упражняются в сложении и вычитании масс, выраженных в единицах одного наименования.

Емкость

С этой величиной и единицей ее измерения — литром учащиеся знакомятся в I классе. Никаких других единиц емкости в началь­ных классах не вводится. Поэтому такие этапы, как переход от одних единиц измерения к другим, сложение и вычитание величин, выраженных в единицах двух наименований, при изучении емкости отсутствуют.

При ознакомлении учащихся с емкостью и ее единицей — лит­ром можно, например, использовать следующие проблемные ситуа­ции:

1. На столе учителя стоят два сосуда с водой: один узкий, другой широкий (уровень воды в обоих сосудах одинаков), два пустых стаканчика разной емкости (обозначим их № 1 и № 2), а также посуда для переливания. Учитель предлагает выяснить с помощью мерки № 1, в каком сосуде больше воды. Учащиеся уста­навливают, что в широком сосуде помещается 10 таких мерок воды, а в узком только 5. Делается соответствующий вывод. Затем с той же целью используется мерка № 2. В широком сосуде поме­щаются 4 такие мерки воды, а в узком — 2. Делается вывод. После этого учитель предлагает измерить количество воды в широком сосуде с помощью мерки № 2, а в узком — с помощью мерки № 1. Обсуждение результатов подводит учащихся к выводу, что для сравнения количества воды в сосудах необходимо пользоваться единой меркой. Полезно и здесь провести сопоставление: так же как длину измеряем сантиметром, массу — килограммом, емкость будем измерять единицей емкости — литром.

2. Два сосуда с водой: один широкий, другой узкий, по при этом уровень воды в узком сосуде выше, чем н широком Учитель задает вопрос: «В каком сосуде больше воды?» Ответы противоре­чивы. Нужно решить проблему: как убедиться, в каком из сосудов больше воды? Учащиеся сами предлагают использовать в качестве мерки третий сосуд. Им будет интересно, если окажется, что и в тот и в другой сосуд налито одинаковое количество воды. Учитель подводит итог: при сравнении емкостей не всегда можно полагать­ся на ощущения — предположение следует проверять измере­нием.

После введения единицы измерения емкости решаются разного рода практические задачи, например: «В одном сосуде 5 л воды, а в другом 3 л. Что нужно сделать, чтобы воды в сосудах стало поровну?» (Можно, например, перелить из первого сосуда во вто­рой 1 л воды, тогда в каждом сосуде станет по 4 л. Или из пер­вого вылить 2 л. И т. д.) «В одном сосуде 3 л воды, а в другом на 2 л больше. Как сделать, чтобы воды во втором сосуде было больше на 1 л?» Так же как и первая, задача требует от ребенка проведе­ния предварительных рассуждений, которые должны предвосхи­тить практический результат. Учащиеся могут предложить долить в первый сосуд 1 л воды; отлить из второго сосуда 1 л; долить в первый сосуд 2 л, а во второй 1 л. Каждый из предложенных спо­собов проверяется практически, т. е. сводится к простым упражне­ниям в измерении емкости. Предложенные задачи вызывают у детей больший интерес, нежели просто задание измерить с по­мощью литровой банки количество воды в сосуде.