ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.04.2024
Просмотров: 241
Скачиваний: 0
СОДЕРЖАНИЕ
1. Методика изучения алгебраического материала в начальных классах школы
1.1. Общие вопросы методики изучения алгебраического материала
1.2. Методика изучения числовых выражений
1.3. Изучение буквенных выражений
1.4. Изучение числовых равенств и неравенств
1.5. Методика изучения уравнений
1.6. Решение простых арифметических задач с помощью составления уравнений
2. Методика изучения геометрического материала в начальных классах
2.1. Время, порядок, задачи изучения темы
2.2.Основные положения методики изучения геометрического материала
2.3. Методика изучения основных геометрических фигур Точка, прямая и кривая линии, отрезок прямой
Ломаная линия, длина ломаной линии, периметр многоугольника
3. Методика изучения величин План
3.2.Время и порядок изучения единиц измерения величин
Время
В соответствии с программой знакомство с этой величиной и единицами ее измерения осуществляется во II- IV классах. Однако, учитывая сложность процесса формирования временных представлений, необходимо с I класса вести работу в этом направлении.
В I классе учащиеся имеют дело с временными понятиями в силу практической необходимости записать число и месяц, определить количество дней в неделе и месяце, длительность урока и перемены и т. п.
Во II классе изучаются такие единицы времени, как час, минута; в III классе - год, месяц, сутки, в IV — секунда и век. Знакомство с единицами времени способствует уточнению временных представлений детей.
Эффективным приемом формирования представлений о единицах времени является использование различных занимательных упражнений, например такого. Учитель предлагает ученикам хлопнуть в ладоши ровно через минуту после того, как хлопнет он. (Многие дети уже знают, что нужно досчитать до 60.) Вызывает у детей интерес и работа с календарем. В учебнике приводится большое количество заданий, которые могут при этом использоваться. В процессе их выполнения дети усваивают количество месяцев в году, дней в неделе и их последовательность.
Большую роль в формировании представлений о единицах времени играют задачи на пропорциональную зависимость между такими величинами, как производительность, общая выработка и время, скорость и время, расстояние и время.
В IV классе обобщаются знания детей о единицах времени и их соотношения. С этой целью используются такие задания:
а) Вырази:
|
В месяцах |
В часах |
В минутах |
В секундах |
|
3 года |
4 сут. |
4 ч |
|
|
6 лет |
2 сут. |
9 ч |
|
|
5 лет 8 мес. |
3 сут.9 ч |
8 ч 45 мин |
2 мин 50 сек |
б) Вырази в более крупных единицах времени: 48 ч, 96 ч, 240 мин, 600 мин.
Площадь
Методика формирования представлений о площади фигуры строится в соответствии с общей методикой формирования представлений о величинах. При этом изучение понятия площади проводится с опорой на привычные для детей представления о том, что каждая фигура занимает определенное — большее или меньшее — место на плоскости.
Для разъяснения рассматриваемого понятия используются демонстрационные или индивидуальные модели различных фигур.
Рис. 3
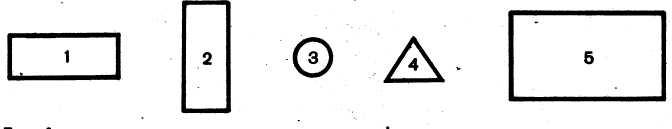

Рис. 4
Путем наложения их друг на друга учащиеся устанавливают, что площади первой и второй фигур одинаковы, а площадь четвертой меньше площади пятой, так как вся четвертая фигура помещается внутри пятой, и т. д. Учитель может предложить выписать номера фигур, расположив их в порядке возрастания площадей. В процессе таких упражнений уточняются представления детей о площади.
После этого учитель может раздать ученикам листы клетчатой бумаги, на которых изображены различные фигуры, например фигуры, представленные на рисунке 4, и предложить сравнить площади этих фигур. Учащиеся сами догадываются, что для этого нужно сосчитать число клеток в каждой фигуре. Фигура, содержащая большее число клеток, имеет большую площадь. Можно предложить учащимся и такой вариант рисунка, чтобы при сравнении площадей изображенных на нем фигур появилась возможность выбрать другую мерку, например треугольник.
Следует обратить внимание учащихся на тот факт, что при сравнении площадей необходимо пользоваться одной и той же меркой. Для этого можно взять демонстрационные модели фигур, каждая из которых разбита на квадраты разных размеров. Учитель предлагает посчитать число квадратов в каждой фигуре. Число квадратов оказывается одинаковым.
- Можно ли утверждать, что площади данных фигур одинаковы? (Нет. Квадраты разные.)
Полезно предложить также и задание, аналогичное тому, которое учащиеся выполняли, когда знакомились с длиной отрезка: «Трое учеников измеряли площадь одной и той же фигуры. В результате первый из них получил в ответе 8, второй — 4, а третий — 2. Почему так могло получиться и кто из них правильно измерил фигуру?» (Фигура предварительно
Рис. 5
чертится в тетради)

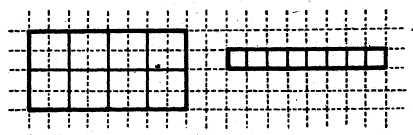
Рис. 6
Учащиеся должны указать на то, что каждый мальчик пользовался своей меркой. Учитель предлагает покрасить эти мерки в разные цвета.
Такого рода задания подводят учащихся к осознанию необходимости введения общепринятой единицы площади 1 кв. см (квадрат со стороной, равной одному сантиметру). У каждого ученика должна быть модель квадратного сантиметра.
Для того чтобы учащиеся освоили процесс измерения площади, полезно раздать им геометрические фигуры и предложить измерить их площади, пользуясь моделью квадратного сантиметра. Это задание особенно важно, так как в процессе его выполнения учащиеся осознают, что измерить площадь фигуры — значит, узнать, сколько квадратных сантиметров она содержит. Учащиеся практически убеждаются в том, что укладывать модель квадратного сантиметра в фигуре долго и неудобно — гораздо удобнее использовать прозрачную бумагу, на которую нанесена сетка из квадратных сантиметров. Таким образом, учащиеся знакомятся с палеткой и правилами пользования ею, упражняются в определении площадей фигур с ее помощью.
При определении площади прямоугольника необходимо также широко использовать практический метод.
М. 3, ч. 1, с. 68
Площадь. Единицы площади
Классная доска висит на стене. Можно сказать, что площадь классной доски меньше, чем площадь этой стены.
Ковёр лежит на полу и полностью его закрывает. Площадь ковра и площадь пола равны.
Площадь
четырёхугольника больше, чем площадь
треугольника. Это видно на
глаз.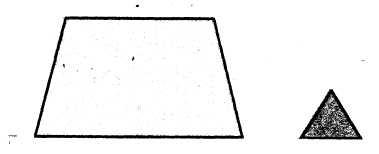
Сравнить площади круга и квадрата на глаз трудно. В таком случае используют способ наложения фигур.
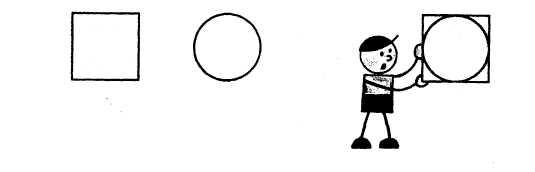
Круг весь поместился внутри квадрата. Значит, площадь круга ... , чем площадь квадрата, а площадь квадрата ... , чем площадь круга.
Часто бывает, что способом наложения сравнить площади фигур нельзя.
В этом случае можно подсчитать квадраты с одинаковой площадью, на которые разбита каждая фигура, и сравнить полученные числа.
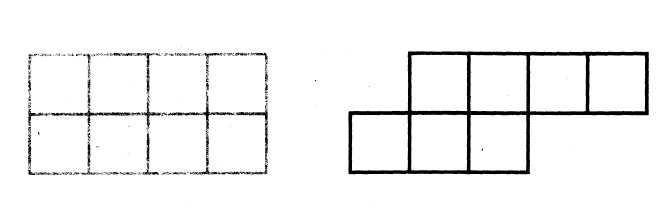
Это поможет учащимся осознать тот факт, что найти площадь прямоугольника — значит узнать, сколько квадратных сантиметров в нем содержится. Однако найти число этих квадратных сантиметров можно рациональнее: путем умножения длины на ширину.
При введении новой единицы площади — квадратного дециметра можно поступить следующим образом: нарисовать на доске прямоугольник и предложить учащимся измерить его площадь, пользуясь двумя моделями — квадратного сантиметра и квадратного дециметра. Учащиеся убеждаются практически, что использование квадратного сантиметра для измерения площади данной фигуры нерационально. Гораздо удобнее пользоваться большей меркой — квадратным дециметром. У каждого ученика должна быть модель квадратного дециметра, разбитая на квадратные сантиметры. Учащиеся самостоятельно устанавливают соотношение между данными единицами площади: 1 кв. дм = 100 кв. см.
При знакомстве с квадратным метром необходимо иметь его демонстрационную модель, разбитую на квадратные дециметры.
Соотношения между единицами площади закрепляются в процессе выполнения различных упражнений.
Арифметические действия с величинами