Файл: Faustova.docx

Многоугольник, угол, круг

Понятия об этих фигурах формируются у детей постепенно в течение всего начального обучения и в последующих классах.

Первоначально, при изучении первого десятка, геометрические фигуры используются как дидактический материал. Опираясь на него, дети учатся считать, вычислять, решать задачи, составлять орнаменты, сравнивать, классифицировать и др. Попутно уточняются представления об отдельных фигурах, запоминаются их названия: круг, треугольник, квадрат.

Далее приступают к изучению отдельных видов многоугольников. На этом этапе вычленяют элементы многоугольников: стороны, углы, вершины. Так, при изучении числа 3 рассматривают различные треугольники. На моделях треугольников, изготовленных из цветной плотной бумаги, пластмассы, дерева и т. п., учащиеся показывают три стороны, три угли и три вершины в каждой фигуре. Затем дети сами моделируют треугольники из палочек и кусочков пластилина или из полосок бумаги; обозначив точками вершины, чертят и раскрашивают треугольники в тетрадях; находят предметы, имеющие форму треугольников; отыскивают треугольники среди других геометрических фигур, начерченных на доске или выставленных на наборном полотне в виде моделей из плотной цветной бумаги. При этом учитель должен позаботиться, чтобы учащиеся рассматривали различные виды треугольников (равносторонние и разносторонние, прямоугольные, тупоугольные и остроугольные). Это поможет формированию правильного представления о треугольнике.

В процессе указанных упражнений дети учатся правильно показывать элементы треугольника: вершины (показывают точки), стороны (показывают отрезки, проводя указкой от одного конца отрезка до другого), углы (показывают угол вместе с его внутренней областью веерообразным движением указки от одной стороны угла до другой, поместив один конец ее вершину угла).

Далее в таком же плане рассматривают четырехугольники, пятиугольники и т. д., приурочивая эту работу к изучению соответствующих чисел в пределах первого десятка. Выделяя элементы многоугольников, учащиеся подмечают связь между числом элементов и названием фигуры (три стороны, три вершины, три угла - треугольник; четыре стороны, четыре вершины, четыре угла - четырехугольник и т. д.). Кроме того, дети осознают, что у многоугольника одинаковое число углов, вершин и сторон. Все эти сведения дети усваивают практически при выполнении заданий с готовыми моделями, при вырезывании, черчении и моделировании многоугольников. Для моделирования лучше использовать набор палочек или бумажных полосок различной длины, чтобы наблюдения не ограничивались равносторонними многоугольниками. Кроме того, дети будут сталкиваться с такими случаями, когда не из любых 3 (4, 5 и т. д.) палочек оказывается возможным построить соответствующий многоугольник.

Понятие многоугольника можно ввести как обобщение рассмотренных видов многоугольников.

В процессе работы над многоугольниками учащиеся получают первые сведения об углах (угол образуют две стороны многоугольника, выходящие из одной из вершин), учатся показывать углы многоугольника.

Далее школьники знакомятся с прямым углом. Это можно провести так. Дети под руководством учителя изготовляют модель прямого угла: они дважды перегибают пополам лист бумаги произвольной формы и устанавливают, что получившиеся при этом две пересекающиеся прямые линии образуют четыре одинаковых угла. Учитель сообщает, что такие углы называют прямыми. Затем дети наложением устанавливают, что, несмотря на различные листы бумаги, все получившиеся прямые углы равны. Пользуясь моделью прямого угла, учащиеся находят прямые и непрямые углы на окружающих предметах, в частности на чертежном треугольнике. В дальнейшем для установления вида угла используют прямой угол чертёжного треугольника (лучше из прозрачной пластмассы): если углы совпадают (т. е. совмещаются их стороны и вершины), то данный угол прямой, если не совпадают - не прямой. Далее рассматривают острые и тупые углы (с.35, 4 кл.).

Для закрепления представления прямого угла включают специальные задания. Например, среди разнообразных данных углов предлагают найти прямые углы; в данных многоугольниках найти прямые углы; начертить прямой угол в тетради, используя ее разлиновку; начертить треугольник (четырехугольник), имеющий прямой угол, и др. Аналогичная работа проводится и с другими видами углов.

Чтобы у детей сформировалось правильное представление угла, наряду с бумажными моделями используют модель «раздвижного угла» (малку). Рекомендуется изготовить каждому ученику такую модель угла из двух палочек, скрепленных кусочком пластилина или гвоздиком. С помощью такой модели дети наглядно убеждаются, что величина угла зависит не от длины его сторон, а от взаимного положения сторон относительно друг друга [1].

Понятие угла закрепляется у учащихся в дальнейшем в процессе изучения многоугольников, например при рассмотрении прямоугольника. Среди нескольких четырехугольников дети с помощью модели прямого угла находят четырехугольники с одним, двумя прямыми углами, а также четырехугольники, у которых все углы прямые. Учитель сообщает, что в последнем случае четырехугольники называют прямоугольниками. Учащиеся находят в окружающей их обстановке предметы прямоугольной формы, показывают прямоугольники среди других геометрических фигур, начерченных на доске или выставленных на наборном полотне, вырезают их из бумаги в клеточку, чертят по точкам в тетрадях и т. п. В процессе таких упражнений у детей формируется наглядный образ прямоугольника, запоминается его название.

На следующем этапе работы учащиеся знакомятся с одним из свойств прямоугольника: противоположные стороны прямоугольника равны между собой. Уточнив сначала, понимают ли дети, какие стороны прямоугольника можно назвать противоположными, учитель предлагает учащимся на бумажных моделях прямоугольника непосредственным наложением сравнить противоположные стороны. Измеряя противоположные стороны прямоугольников, данных в учебнике и на доске, дети

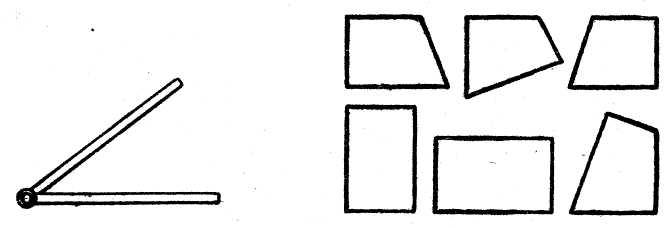
также подтверждают и обобщают свои наблюдения. Знание этого свойства сторон прямоугольника закрепляется в дальнейшем, когда учащиеся чертят прямоугольники по двум заданным его сторонам (длине и ширине). В I - IV классах учащиеся выполняют построение прямоугольников с помощью линейки (чертят прямые углы, пользуясь разлиновкой тетрадей).

После того как учащиеся усвоят свойство противоположных сторон прямоугольника, из множества прямоугольников вычленяют квадраты - прямоугольники с равными сторонами.

Работа на уроке так и организуется, чтобы учащиеся увидели, что квадрат-это частный случай прямоугольника. Детям предлагается, например, измерить стороны у нескольких прямоугольников, начерченных на доске или вырезанных из бумаги. Среди них обнаруживаются такие прямоугольники, у каждого из которых стороны равны между собой. Дети сами вспоминают их название - квадраты. Чтобы подчеркнуть, что квадраты - это прямоугольники с равными сторонами, включают такие задания: «Покажите прямоугольники, которые нельзя назвать квадратами; найдите среди данных четырехугольников четыре прямоугольника; найдите среди указанных прямоугольников два квадрата и т. п.». В подобных заданиях дети должны обосновывать свои суждения, промеряя с помощью чертежного треугольника, являются ли все углы четырехугольника прямыми, а также устанавливая с помощью линейки, каково в нем соотношение сторон.

Большое значение для закрепления представлений о многоугольниках, а также для развития пространственных представлений в целом имеют задачи с геометрическим содержанием, которые включаются систематически. Это задачи на деление заданных фигур так, чтобы получившиеся части имели указанную форму; задачи на составление новых фигур из данных многоугольников (т. с. конструирование целого из частей), а также задачи на распознавание (вычленение) всевозможных геометрических фигур на заданном чертеже. Все эти задачи взаимосвязаны друг с другом. Решение задач каждого вида помогает при решении задач других видов.

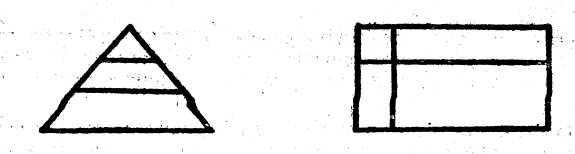
Поэтому они включаются, перемежаясь в определенной системе, так что число частей фигуры (из которых она составляется или на которые расчленяется) увеличивается постепенно. Например, разрежьте квадрат так, чтобы получилось два прямоугольника (два треугольника), а потом 4 треугольника, четыре квадрата и т. п.; из двух (а затем из четырех) треугольников (полученных, например, при разрезании квадрата по его диагоналям) сложите треугольник, четырехугольник и т. и., при этом вначале дают образец тех фигур, которые должны получиться при составлении (или при разрезании), а потом уже задание выполняется без образца. При вычленении знакомых фигур на чертеже сначала указывают, сколько и каких фигур надо показать: найдите на чертеже 3 треугольника и 3 четырехугольника, а потом задание усложняется, например: сосчитайте, сколько всего прямоугольников изображено ни чертеже, или так: какие знакомые фигуры вы видите на чертеже и сколько их. При выполнении таких заданий по учебнику можно дать задания по вариантам, а затем предложить проверить учащимся друг друга. После этого вызванные учащиеся показывают фигуры по чертежу на доске, а остальные проверяют правильность выполнения.

Начиная с III класса, когда учащиеся ознакомятся с обозначениями фигур буквами, подобные задания выполняются с записью решений и необходимых построений в тетрадях.

В процессе решения таких задач у детей формируются умения воспринимать многоугольник, составленный из частей, и в то же время видеть многоугольники, являющиеся частями другого многоугольника; вырабатывается наблюдательность, зоркость, умение мысленно конструировать геометрические фигуры.

В III классе учащиеся знакомятся с окружностью, учатся чертить окружности с помощью циркуля, знакомятся с элементами окружности и круга — центром, радиусом и диаметром( ч. 1, с.94). Все эти сведения усваиваются детьми в процессе выполнения практических заданий. Например, соединив точки, лежащие на окружности, с центром и сравнив полученные отрезки, дети убеждаются в равенстве этих отрезков. Вводится название таких отрезков — радиус круга или окружности.

Сопоставив круг с многоугольником, учащиеся устанавливают, что границей многоугольника является замкнутая ломаная линия, а границей круга - замкнутая кривая линия - окружность.

Чтобы учащиеся не смешивали круг и окружность, дают специальные задания, например: проведите окружность и раскрасьте круг, отметьте центр круга или окружности, а также точки, лежащие внутри круга, вне круга, на окружности.