ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.04.2024
Просмотров: 385
Скачиваний: 0
СОДЕРЖАНИЕ
Елецкий государственный университет им. И.А. Бунина
§ 1. Функции арифметических задач в обучении математике младших школьников
§ 2. Понятие арифметической задачи. Её структура
§ 3. О классификации арифметических задач, решаемых в начальных классах
§ 4. Анализ процесса решения задачи
§ 5. Свойства полноценного умения решать арифметические задачи
§ 6. Общие вопросы методики формирования умения решать арифметические задачи
Выполнение записи решения задач
Закрепление умения решать задачи рассматриваемого вида
§ 7. Методика обучения решению простых арифметических задач
7.3. Задачи на нахождение неизвестных уменьшаемого, вычитаемого, слагаемого
Задача на нахождение неизвестного слагаемого
Задача на нахождение неизвестного уменьшаемого
Задача на нахождение неизвестного вычитаемого
Задачи на нахождение произведения
Задачи на деление по содержанию и на равные части
Задачи на уменьшение числа в несколько раз, выраженные в прямой форме
§ 8. Методика введения первых составных арифметических задач
9.1. Задачи на нахождение четвёртого пропорционального
9.2. Задачи на пропорциональное деление
9.3. Задачи на нахождение неизвестных по двум разностям
9.4. Задачи, связанные с движением
Семестровые задания(представляются к летней сессии, 6 семестр)
Методика обучения математике младших школьников ( вопросы частной методики, часть 2)
Выделяют два вида формального разбора: разбор от вопроса к числовым данным; разбор от данных к вопросу.
Чтобы научить школьника самостоятельно осуществлять поиск решения задачи, методисты разрабатывают «памятки» по решению задач, которые отображают систему операций по её решению. Этими памятками дети пользуются в процессе решения задач сначала с помощью и под руководством учителя, а затем самостоятельно.
При обучении решению простых арифметических задач можно использовать следующие памятки [18]:
а) При решении первых простых арифметических задач:
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Рисую и объясняю...
4. Подумаю, надо объединять или удалять...
5. Подумаю, надо прибавлять или вычитать...
6. Выполняю решение...
7. Отвечаю на вопрос задачи...
б) При решении различных видов простых арифметических задач:
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Запишу задачу кратко...
4. Подумаю, большее или меньшее число надо находить...
5. Подумаю, каким действием...
6. Выполняю решение...
7. Отвечаю на вопрос задачи...
8. Проверяю...
При обучении решению составных арифметических задач считаем целесообразным использовать два вида памяток:
1) Разбор от вопроса к числовым данным.
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Запишу задачу кратко...
4. Подумаю, что нужно знать, чтобы ответить на вопрос задачи...
5. Каким действием?
6. Подумаю, могу ли сразу ответить на вопрос задачи?
Почему?
(Операции 4-6 выполняются столько раз, сколько арифметических действий в задаче.)
7. Составляю план решения.
8. Выполняю решение.
9. Отвечаю на вопрос задачи.
10. Проверяю.
2)Разбор от числовых данных к вопросу.
Рассуждаю так:
1. Мне известно...
2. Надо узнать...
3. Запишу кратко задачу...
4. Выделяю два данных числа...
5. Подумаю, что можно узнать по этим данным...
6. Каким действием?
(Операции 4-6 выполняются столько раз, сколько арифметических действий в задаче.)
7. Составляю план решения...
8. Выполняю решение...
9. Отвечаю на вопрос задачи...
10. Проверяю.
Кроме памяток, являющихся вербальными моделями способов деятельности по решению составных арифметических задач, мы сочли необходимым при обучении детей этой возрастной группы решению данных задач использовать схематическую модель способа деятельности по решению составной арифметической задачи, так называемую «схему размышления». Она отображает в наглядной форме всю последовательность операций, выполняемых при решении составной арифметической задачи. Приведём примеры полного рассуждения ученика при разборе задачи от вопроса к числовым данным и от числовых данных к вопросу с использованием схем размышления.
Задача. Во дворе играли 5 девочек и 4 мальчика. Сколько детей осталось играть во дворе, если 6 детей ушло?
1) Полное рассуждение ученика при разборе от вопроса к числовым данным.
1. Мне известно, что играли во дворе 5 девочек, 4 мальчика и что 6 детей ушли.
2. Надо узнать, сколько детей осталось играть во дворе.
3. Запишу задачу кратко.
В задаче главные слова: играли, ушли, осталось.
Играли - 5 дев. и 4 мал.
Ушли - 6 дет.
Осталось - ? дет.
Главный вопрос задачи подчёркиваю.
4. Чтобы узнать, сколько детей осталось играть, надо знать, сколько детей играли и сколько детей ушли.
(Изображает часть схемы:
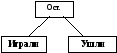 ?
?
).
5. Если я буду знать, сколько всего детей играло и сколько ушло, то смогу узнать, сколько осталось играть действием вычитания (ставит в схеме знак «-»).
6. Сразу узнать, сколько детей осталось играть, я не могу, потому что не знаю, сколько всего детей играло (ставит в схеме около «Играли» знак вопроса).
4а. Чтобы узнать, сколько всего детей играло во дворе, надо знать, сколько играло мальчиков и сколько девочек (изображает в схеме).
5а. Если я буду знать, сколько играло девочек и сколько мальчиков, то смогу узнать, сколько всего детей играло действием сложения (ставит в схеме знак «+»).
6а. Я могу сразу узнать, сколько всего детей играло, потому что знаю, что девочек играло 5, мальчиков - 4.
7. Составляю план решения. Сначала действием сложения узнаю, сколько всего детей играло, потом действием вычитания узнаю, сколько детей осталось играть (ставит в схеме соответственно цифры 1 и 2 над знаками действий).
Схема приобретает вид:
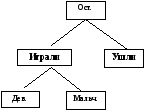 ?
?
? 2
-
1
+ +
(О2 — АД2 — О1 — АД1 — АД1 — АД2 )
2) Разбор от числовых данных к вопросу.
Выполним только операции, начиная с 4.
4. Знаю, что девочек было 5, мальчиков 4.
5. Могу узнать, сколько играло всего детей.
6. Действием сложения.
4а. Буду знать, сколько всего играло и знаю, что 6 детей ушли.
5а. Смогу узнать, сколько детей осталось играть, отвечу на главный вопрос задачи.
6а. Действием вычитания.
Одновременно также можно выполнить схему, отображающую процесс поиска решения задачи:
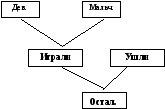
1
+
2
-
В методической литературе даются всевозможные памятки, но, на наш взгляд, они не отображают полностью деятельность ребёнка по решению задачи, т.е. не являются моделью этой деятельности. Поэтому их использование не обеспечивает требуемой эффективности процесса обучения решению задач.
Выполнение записи решения задач
Большинство простых арифметических задач решается устно, на этапе ознакомления запись решения осуществляется всегда.
Приняты следующие формы записи решения задачи.
Рассмотрим на примере ранее рассмотренной составной арифметической задачи.
1) Запись решения задачи с помощью составления математического выражения:
а) по ступенькам без письменных пояснений:
5 + 4 (дет.),
(5 + 4 ) - 6 (дет.),
(5 + 4) - 6 = 3 (дет.).
Ответ: осталось играть 3 детей.
б) по ступенькам с письменными пояснениями:
5 + 4 (дет.) - столько играло,
(5 + 4) - 6 (дет.) - столько осталось играть,
(5 + 4) - 6 = 3 (дет.).
Ответ: 3 детей.
в) сразу выражением с письменными пояснениями:
(5 + 4) - 6 = 3 (дет.) - столько осталось играть.
Ответ: 3 детей.
г) сразу выражением без письменных пояснений:
(5 + 4) - 6 = 3 (дет.)
Ответ: осталось играть 3 детей.
2) Запись решения задачи отдельными действиями:
а) с письменными пояснениями:
1. 5 + 4 = 9 (дет.) - столько играло,
2. 9 - 6 = 3 (дет.) - столько осталось играть.
Ответ: 3 детей.
б) без письменных пояснений:
1) 5 + 4 = 9 (дет.)
2) 9 - 6 = 3 (дет.)
Ответ: осталось играть 3 детей.
Согласно программе 1-1У запись решения первых составных арифметических задач выполняется с помощью составления выражения.
Кроме арифметического способа решения задач, простые арифметические задачи II группы, начиная с 4 класса, могут решаться алгебраическим способом. Запись решения в этом случае осуществляется с помощью составления уравнения. Могут быть те же формы (см. 1) а) - г)), что и при решении задачи арифметическим путём. Рассмотрим форму записи решения 1б.
Задача. После того, как с аэродрома улетело 4 вертолёта, там осталось 2 вертолёта. Сколько вертолётов было на аэродроме?
Х (в.)- столько было на аэродроме,
Х-4 (в.)- столько осталось на аэродроме,
2 (в.) - столько осталось на аэродроме.
Составляем уравнение: Х-4=2
Решение уравнения:
Х-4=2
Х=4+2
Х=6
6-4=2
2=2
Ответ: 6 вертолётов.
Памятка при решении простой арифметической задачи с помощью составления уравнения может быть следующей:
Рассуждаю так:
1. Подумаю, что обозначу за Х.
2. Подумаю, что буду уравнивать.
3. Составляю два выражения, являющимися значениями одной и той же величины.
4. Записываю уравнение.
5. Решаю уравнение.
6. Проверяю.
Проверка решения задачи
В начальных классах методисты рекомендуют пять способов осуществления проверки правильности решения задачи [1,22].
1)Установление соответствия полученного результата условию задачи.
При проверке решения задачи этим способом выполняют арифметические действия над числами, которые получатся в ответе на вопрос задачи; если при этом получатся числа, данные в условии задачи, то можно считать, что задача решена правильно.
Рассмотрим применение этого способа для проверки решения следующей задачи: «В первый ларёк привезли 6 ящиков апельсинов, а во второй 4 таких же ящика. Сколько килограммов апельсинов привезли в каждый ларёк, если всего привезли 90 кг?».
В результате решения этой задачи ученики найдут, что в первый ларёк привезли 54 кг апельсинов, а во второй - 36 кг апельсинов. Для проверки правильности решения надо установить, будет ли в двух ларьках 90 кг. Проверяем 54+36=90 (кг). Число, полученное в ответе соответствует данному. Значит, можно считать, что задача решена правильно. Этот способ проверки используется, начиная со второго класса. Его целесообразно применять для проверки решения задач такой структуры, в которых можно получить числа, данные в задаче, путём выполнения соответствующих арифметических действий над числами, полученными в ответе (задачи на пропорциональное деление, на нахождение неизвестного по двум разностям и др.).
2) Составление и решение обратной задачи.
В этом случае детям предлагается составить и решить задачу, обратную по отношению к данной задаче. Если при решении обратной задачи в результате получится число, которое было известно в данной задаче, то можно считать, что задача решена правильно.
Этот способ вводится во втором классе, лишь бы обратная задача была посильна детям. В связи с этим детям надо указывать, какое число можно брать искомым в обратной задаче. Безусловно, не надо решение всех задач проверять способом составления обратной задачи: он очень громоздок, труден, решение обратной задачи может оказаться труднее данной.
Однако, во многих случаях очень полезны сами упражнения в составлении и решении обратных задач, поскольку они помогают уяснить связи между данными задачи. В связи с этим целесообразно проверять этим способом решение всех простых задач, задач на нахождение четвёртого пропорционального, задач, в которых находится сумма, разность или частное двух произведений и других задач.