ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.04.2024
Просмотров: 144
Скачиваний: 0
СОДЕРЖАНИЕ
Б. 2 в. 1 Необходимые условия экстремума функции нескольких переменных. Достаточные условия
4.Формула Тейлора с остаточным членом в форме Лагранжа. Разложение элементарных функций.
Б.2 в. 5 Ряд Лорана. Классификация изолированных особых точек. Вычеты.
8 Теорем Рисса о представлении линейного функционала
Б.2 в. 14 Корректность постановки задач математической физики. Привести пример.
Дифференциальным уравнением называется уравнение, содержащие производные неизвестных функций.
Б.2 в.19 Функция Грина. Функция Грина для внутренней задачи Дирихле.
Док-во
По теор1![]() и
при том только одна точка х
и
при том только одна точка х![]() Х.
g1(x)=x.Применим
к обеим частям рав-ва отобр g,воспольз
тем,что отобр-ия коммут-т,получим
g(g1(x))=
g(x)
Х.
g1(x)=x.Применим
к обеим частям рав-ва отобр g,воспольз
тем,что отобр-ия коммут-т,получим
g(g1(x))=
g(x)![]() ,где
у=g(x).Учитывая,что
отобр-е g1
сжимающее и неподвижная точка у этого
отображения одна,получим,что
х=у=g(x),следовательно
и у отобр-я g
сущ-ет неподвижная точка,а именно
найденная выше точка х=g(x).
,где
у=g(x).Учитывая,что
отобр-е g1
сжимающее и неподвижная точка у этого
отображения одна,получим,что
х=у=g(x),следовательно
и у отобр-я g
сущ-ет неподвижная точка,а именно
найденная выше точка х=g(x).
Пример Рассмотрим задачу Коши. Треб-ся найти такую дифф-ую фун-ю y(t),кот-я удовл-ла бы уравнению y′=f(t,y) и при t=t0 имела заданное значениe y(t0)=y0,где y0 некоторое число. При этом надо док-ть,что при опред-ых условиях такое решение y(t)одно.
Док-во
Предпол-м,что фун-ия f(t,y)
непрерывна на множ-ве a≤t≤b,
-![]() <y<
<y<![]() и удовл-ет условию Липшица по у: (
и удовл-ет условию Липшица по у: (![]() <K
<K
![]() где K=сonst.Пусть
t0-внутр.точка
где K=сonst.Пусть
t0-внутр.точка![]()
Реш-е зад. Коши
эквив. реш. инт. ур-я
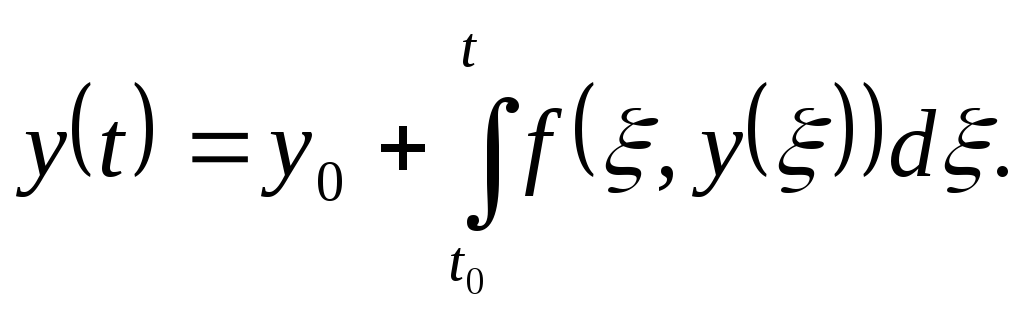 Т.о.задано отобр.
Т.о.задано отобр.
фун-ии множ-ва {y}
по правилу
 Введем
в рассмотр простр-во С[a,b],тогда
отобр-е g
определено на этом пр-ве и отбр-ет его
в себя,а задача о нах-ии реш-я интнгр-го
yр-я
свод-ся к нах-ию неподв-ой точки отобр-я
g,т.е.
нах-ю такой фун-ии у/ g(у)=у.Для
того,чтобы такая точка
Введем
в рассмотр простр-во С[a,b],тогда
отобр-е g
определено на этом пр-ве и отбр-ет его
в себя,а задача о нах-ии реш-я интнгр-го
yр-я
свод-ся к нах-ию неподв-ой точки отобр-я
g,т.е.
нах-ю такой фун-ии у/ g(у)=у.Для
того,чтобы такая точка
![]() и была единств-й достат-но,чтобы отобр-е
g
было сжимающ-м.Поскольку из условия
Липшица следует,что
и была единств-й достат-но,чтобы отобр-е
g
было сжимающ-м.Поскольку из условия
Липшица следует,что
![]() ,то
,то
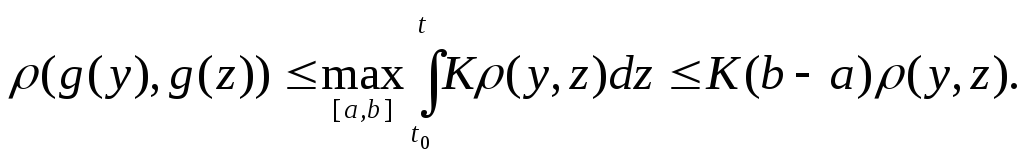 Здесь
ρ-метрика в С[a,b],следоват
отобр-е сжимающее,если [a,b]
достаточно мал, K(a-b)=θ<1.При
этих усл-ях получаем теор сущ-ия и
единств-ти реш-я задачи Коши на [a,b]
сод-т точку t0.
Здесь
ρ-метрика в С[a,b],следоват
отобр-е сжимающее,если [a,b]
достаточно мал, K(a-b)=θ<1.При
этих усл-ях получаем теор сущ-ия и
единств-ти реш-я задачи Коши на [a,b]
сод-т точку t0.
№7. Пусть
X,
Y
мн-ва произв-й природы.D![]() X
X
Опр.1
Если каждому эл-ту x![]() D
ставится определ.эл-т у
из Y,
то гов-т, что
задан оператор y=F(x),при
этом мн-во D
наз. обл. опред-я оператора F
и обозн.D(F).Мн-во
R=R(F)=
D
ставится определ.эл-т у
из Y,
то гов-т, что
задан оператор y=F(x),при
этом мн-во D
наз. обл. опред-я оператора F
и обозн.D(F).Мн-во
R=R(F)=![]() наз.
обл. знач-й оператора F
наз.
обл. знач-й оператора F
Схематич. действие
операт. F
м. изобр.![]() образом:X
образом:X![]() что
кратко зап-т так:F:X
что
кратко зап-т так:F:X![]() Y.Если
y=F(x),
x
Y.Если
y=F(x),
x![]() D(F),у
D(F),у![]() R(F),то
гов-т, что у
явл-ся образом эл-та х,а
х прообразом
эл-та у.
R(F),то
гов-т, что у
явл-ся образом эл-та х,а
х прообразом
эл-та у.
Опр2
Два оператора
F:X![]() Y
и Ф:X
Y
и Ф:X![]() Y
наз-ся равными,если совп-т их области
определ-я D(F)=
D(Ф)иF(x)=Ф(х).
Y
наз-ся равными,если совп-т их области
определ-я D(F)=
D(Ф)иF(x)=Ф(х).
Опр3
Опер-р y=F(x)
наз-ся
взаимооднозн,если каждому образу у![]() R(F)
соотв-ет единственный прообраз х=F-1(y).
R(F)
соотв-ет единственный прообраз х=F-1(y).
Если F
взаимноодн-но,то ф-ла х=F-1(y),
у![]() R(F)
опред-т
опер-р F-1:Y
R(F)
опред-т
опер-р F-1:Y![]() X,кот
наз обратным к F.Область
опред-я D(F-1)=
R(F),а
R(F-1)=
D(F).
X,кот
наз обратным к F.Область
опред-я D(F-1)=
R(F),а
R(F-1)=
D(F).
Пусть X,
Y
нормир-ые
простр-ва. Пусть дан опер-р F:X![]() Yтакой,что
его область опр
D(F)
Yтакой,что
его область опр
D(F)![]() S(x0)
точки х0,за
искл-м самой этой точки.
S(x0)
точки х0,за
искл-м самой этой точки.
Опр4
Эл-т у0![]() У
наз-ся пределом опер-ра F
в точке х0,если
У
наз-ся пределом опер-ра F
в точке х0,если
![]() можно
ук-ть δε>0/
можно
ук-ть δε>0/![]() и
из выполн-я нер-ва ||x-x0||<
δε
след-ет выполнимость нер-ва ||F(x)-y0||<ε,y0=
и
из выполн-я нер-ва ||x-x0||<
δε
след-ет выполнимость нер-ва ||F(x)-y0||<ε,y0=![]()
Опр5
Пусть дан опер. F:X![]() Y,опер.Fназ.непрер.в
(.)x0,если
F(x)
Y,опер.Fназ.непрер.в
(.)x0,если
F(x)![]() F(x0),
F(x0),
x![]() x0
x0
Опр6
Пусть F(x)
оператор с обл опр-я D(F)
и значений
R(F),где
D(F)![]() X,
R(F)
X,
R(F)
![]() Y
и пусть X
и
Y
норми-ые пр-ва.Опер-р F
наз-т огранич-м,если он переводит всякое
огранич-е множ-во из D(F)
в огранич-е
множ-во Y.
Y
и пусть X
и
Y
норми-ые пр-ва.Опер-р F
наз-т огранич-м,если он переводит всякое
огранич-е множ-во из D(F)
в огранич-е
множ-во Y.
Опр7
Опер-р A:X![]() Y
c
D(A)
наз-ся
линейным,если:а)
D(A)линейное
многообразие;б)
Y
c
D(A)
наз-ся
линейным,если:а)
D(A)линейное
многообразие;б)![]() D(A)
А(λ1х1+λ2х2)=
λ1А
х1+λ2
А
х2,
λ1
,λ2-любые
скаляры.
D(A)
А(λ1х1+λ2х2)=
λ1А
х1+λ2
А
х2,
λ1
,λ2-любые
скаляры.
Опр8
Опер-р А
наз-ся непрер в точке х0
![]() Х,если
Ах
Х,если
Ах![]() Ах0при
x
Ах0при
x![]() x0.
x0.
Теорема Пусть
линейн опер-р А
задан всюду в банаховом пр-ве Х
со значениями в банах-м пр-ве У
и непрер в точке 0![]() Х,тогда
опер А
непрер-н в любой точке x0
Х,тогда
опер А
непрер-н в любой точке x0
![]() Х.
Х.
Док-во Док-во
след-т из рав-ва
![]() и
следоват-но при x
и
следоват-но при x![]() x0
x0
Ах-Ах0.Т.о.теорема док-на.
Опр9 Линейн опер-р А явл-ся непрер,если он непрер-н в точке х=0.
Опр10 Линейн
опер А с
D(A)=Х
и R(A)![]() X
ограничен,если
он огр-н на единичном шаре,т.е. если
огр-но мн-во норм {||Ax||,||x||≤1}.Отсюда
следует,что если опер А огр,то
X
ограничен,если
он огр-н на единичном шаре,т.е. если
огр-но мн-во норм {||Ax||,||x||≤1}.Отсюда
следует,что если опер А огр,то
![]() с=const>0
с=const>0
![]() х
удовл нер-во ||x||≤1
||Ax||≤c.
х
удовл нер-во ||x||≤1
||Ax||≤c.
Теорема
Опер А
огр-н тогда и только тогда,когда спр-ва
оценка ||Ax||≤c||x||,
где х![]() Х,с=const
определ из нер ||x||≤1
||Ax||≤c.
Х,с=const
определ из нер ||x||≤1
||Ax||≤c.
Док-во При х=0 нерво||Ax||≤c||x|| очевидно.
Пусть х≠0. Положим
х′=![]() .||x′||=1,поэтому
из нер-ва ||Ax||≤c||x||
.||x′||=1,поэтому
из нер-ва ||Ax||≤c||x||![]() что
что
![]() тогда
тогда
![]() По св-ву линейности
По св-ву линейности
![]() ,поэтому
,поэтому
![]() .Т.о.
.Т.о.
![]()
Теорема Пусть
![]() -
огр мн-во,тогда {||Ax||,x≤М}-огр-но.
-
огр мн-во,тогда {||Ax||,x≤М}-огр-но.
Теорема
Пусть
A:X![]() Y,А-лин-й
опер-р, X,Y
Банаховы пр-ва,
D(A)=Х.
Для того,чтобы
опер-р был непр-н необх-мо и дост-но,чтобы
он был огран-ым.
Y,А-лин-й
опер-р, X,Y
Банаховы пр-ва,
D(A)=Х.
Для того,чтобы
опер-р был непр-н необх-мо и дост-но,чтобы
он был огран-ым.
8 Теорем Рисса о представлении линейного функционала
Теорема
Пусть Н-гильбертово
пространство (комплексное или вещественное)
Для любого линейного ограниченного
функционала f заданного всюду на Н
существует единственный элемент
![]() такой
что для всех
такой
что для всех
![]()
![]()
При этом ||f||=||y||
Доказательство
Рассмотрим L
–множество всех элементов
![]() таких
что
таких
что
![]()
Если L=H то f=0 можно взять y=0 и теорема доказана
Пусть
![]() тогда найдется
тогда найдется
![]() причем можно считать что <z_0,f>=1
Пусть теперь
причем можно считать что <z_0,f>=1
Пусть теперь
![]() тогда
x-<x,f>z_0
тогда
x-<x,f>z_0![]() так как
так как
![]()
Следовательно
![]() откуда
откуда
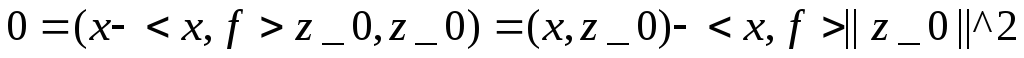
отсюда
![]() Итак можно принять
Итак можно принять
![]()
Покажем что ||f||=||y|| Действительно
![]()
По неравенству
Коши-Буняковского Из определения нормы
f
имеем
![]() Но
кроме того
Но
кроме того
![]()
Откуда
![]() Итак
||f||=||y||
Итак
||f||=||y||
Осталось доказать
единственность y.
Если
![]() то
то
![]() для
любых
для
любых
![]() Возьмем
Возьмем
![]() и получим
и получим
![]() ЧТД
ЧТД